4.3.3Метод цепных подстановок.

Исходная формула та же : =

1) =

2) =Pвб =73,01 =3,556

3) =73.01

Pa-

Анализ в составе to.

1. = 17,124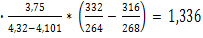

= ;

а) = = =1,034

б) = = =0,308

2. = 17,124

а) = = =0,534

б) = = =0,202

3) = 17,124

Дифференцировать можно время оборота по параметрам: время погрузки, выгрузки; производительности погрузки, выгрузки; ожиданий погрузки, выгрузки. Однако, цепная подстановка, в силу множественности вычислений приводит к погрешностям, а самое главное, существенно влияет фактор, с которого начинается анализ. В сумме результат один и тот же, а влияние факторов различное.

4.3.4. Статические приемы изучения взаимосвязи количественных показателей (корряляционный регрессионный методы анализа).

Этот метод призван решать следующие задачи:

1. Выявить зависимость признаков;

2. Установить форму связи и находить ее аналитическое выражение, измерять степень тесноты связи;

3. Рассчитывать теоретические уровни, анализировать результаты.

Первая задача – предполагает логическую обработку первичного материала, отбор факторов, влияющих на результативный признак, выявление зависимостей с помощью метода группировок.

Вторая задача – предполагает измерение степени тесноты связи с помощью коэффициента корреляции с целью суждения об адекватности полученной модели данному экономическому процессу или явлению.

Третья задача- состоит в том, чтобы по полученному уравнению регрессии находить теоретические уровни, т.е. плановые показатели на предстоящий период. Цель – научно обоснованное нормирование и краткосрочное планирование.

Термин «корреляция» от латинского «correlation» - соотношение, заимствована из естествознания. Суть в том, что значение факторного признака соответствует не строго определенные значения результативного признака, как функциональных связях, а распределение этих значений.

Термин «регрессия» - заимствовано из биологии, от латинского «regressio» - движение назад.

Корреляционно – регрессионный метод исследования состоит из двух этапов.

Корреляционный метод решает следующие задачи:

- выявить зависимость между признаками;

- установить форму связи и находить ее аналитическое выражение;

- измерять степень тесноты связи.

Регрессивный метод решает следующие задачи:

- дает выражение в аналитической форме связи в виде управления связи (регрессии);

- на основании этого выражения рассчитываются ожидаемые или планируемые показатели на предстоящий период.Исходные эмпирические (фактические) данные наносим на графике корреляционного поля и на основании графика делаем вывод о форме Связи. На оси абсцисс откладываем факторные значения призна­ка, а на оси ординат результативные.

Рассмотрим три случая на графике корреляционного поля.

У У У

П рямая линейная зависимость

Х Х Х

Обратная линейная зависимость

З ависимость

отсутствует

Графики корреляционных полей

Построив график по эмпирическим значениям обоих признаков, делаем вывод о форме связи, ее направлении, а по разбросу точек - о тесноте связи.

Прежде чем перейти к построению уравнения регрессии необхо­димо определить коэффициент корреляции парной или множественной, с тем чтобы убедиться в необходимости дальнейших расчетов.

Следующим этапом исследования является количественное опре­деление степени влияния факторных признаков на результативный. Ме­рой существенности влияния являются показатели тесноты связи: ли­нейный коэффициент корреляции (г) при прямолинейной форме связи и корреляционное отношение (п) при криволинейной форме связи, кото­рые дают возможность судить в будущем о соответствии полученной экономико-статистической модели экономическому процессу или явле­нию.

Линейный коэффициент корреляции обозначается «г» и изменяет­ся при прямой связи от 0 до+1, а при обратной связи - от 0 до -1. О тес­ноте связи свидетельствует абсолютная величина коэффициента корре­ляции. Чем теснее связь между признаками, тем ближе к единице будет значение линейного коэффициента корреляции и наоборот. Для качест­венной оценки связи используется таблица Чеддока (табл.4.1):

Значение коэффи-	0,3-0,3	03-0,5	0,5-0,7	0,7-0,9	0,9-0,99
циента
Характеристик	слабая	умеренная	заметная	высокая	Весьма
тесноты					высокая
связи

Табл 4.1 Таблица Чеддока

При наличии криволинейной связи «г» недооценивает тесноту свя­зи и в некоторых случаях дает неверное представление о степени тесно­ты связи.

На этом заканчивается первый этап исследования - корреляцион­ный анализ, который позволил определить направление, форму и силу тесноты связи. Результаты корреляционного анализа служат основой для проведения регрессионного анализа, дающего выражение аналитической форме связи в виде построения теоретического уравнения регрессии.

В качестве примера, приведем расчеты выполненные в конце 1999 года для ЛЦББ (Ленская Центральная Бассейновая больница).

Как правило, исследуемые процессы характеризуются большой сложностью и многообразием, и представляют собой результат действия: многих факторов. Поэтому, чтобы отразить это влияние на результирующий признак, необходимо производить расчеты на основе методов множественной корреляций. Однако в нашем случае, во-первых, в ЛЦББ просто нет соответствующей статистики, ее надо формировать для исследований в будущем. А. во-вторых, это очень громоздкие расче­ты даже для ЭВМ, при условии, что существует соответствующее матемагическое обеспечение, т.е. готовые программы этого метода. Но смысл корреляционно-регрессионного анализа не теряется, если для уп­рощения расчетов будем исходить из двухфакторного комплекса, т.е. та­кая постановка задачи выполнена выше. В расчетах будут участвовать два признака, на результативный будет действовать один факторный признак.

При анализе должно выполняться основное условие - соблюдение качественной и количественной однородности единиц наблюдения, ко­торое обеспечивает получение регрессионной модели, адекватной эмпи­рическим данным (статистическому материалу).

Выполнив логическую обработку первичного материала ЛЦББ по всем ее структурным подразделениям - центральной больнице и линей­ным больницам, приходится констатировать, что условие соблюдения качественной и количественной однородности единиц наблюдения не соблюдается. Причина в том, что уровень зарплаты медперсонала по всем больницам совершенно различный, в силу того, что на Верхней Лене иные районные коэффициенты и северные надбавки в сравнении с Якутией, а в самой Яхутии они так же различны.

Например, в Пеледуе, Якутске, Нижне-Янске. Кроме того, не по­следнюю роль играет отношение руководства предприятий и админист­рации тех поселков где дислоцированы больницы на уровне доходов медперсонала, особенно в последние годы.

Для получения регрессионной модели, для всего бассейна в целом, необходимо разработать методику приведения эмпирического материала по каждой больнице в сопоставимые условия с Ленской центральной бассейновой больницей. Работа эта сложная и долговременная. Поэтому, принято решение, для соблюдения условия однородности как качест­венной, так и количественной эмпирического материала, построить рег­рессионные модели для каждой структурной единицы отдельно.

Выполняются соответствующие расчеты для каждой больнице на статистическом материале за последние 4 года.

Для центральной больницы в Якутске формируем расчетную табл.4.2 для нахождения линейного коэффициента корреляции и парамет­ров уравнения регрессии.

X	У
Объем ме-	Расходы по
дицинских	заработай	ХУ	X2	У2	Ух
услуге	плате мед-
койко-	персонала.
дня х,	тьс.руб.
тъс.койко-
дней
46540	22258	1035887320	2165971600	495418564	22156
50728	36020	1827222560	2573329984	1297440400	36395
53591	46410	2487158310	2871995281	2153888100	4Й129
52952	43911	2325175272	2803914304	1928175921	4? 956
∑Х	∑У	∑ХУ	∑X2	∑У2
203811	148599	7675443462	10415211169	5874922985

Табл 4.2 Расчетная таблица для «г» и уровня регрессии

Линейный коэффициент корреляции для парной зависимости ис­числяется по следующей формуле:

п - количество точек в выборке.

Существуют и другие модификации этой формулы. Подставляя значения в формулу, получим 0,69, что свидетельствует о высокой тес­ноте связи между изучаемыми признаками, а знак при коэффициенте «плюс» -о прямой связи.

В целях синтезирования модели у от х определите уравнение пря­молинейной связи и нанесите полученную при этом теоретическую ли­нию регрессии на график корреляционного поля.

Уравнение прямой линии имеет вид:

Ух = ао + а1 *х;

где У_х - индивидуальные значения результативного признака;

х - индивидуальные значения факторного признака;

ао, а1- параметры уравнения регрессии;

Способом наименьших квадратов решим систему нормальных уравнений, находя параметры ао и а1:

nа_о + а1•∑x = ∑у

а₀ + а1• = ∑xy

4а_о+а1• 203811 = 148599

20381 1 а₀ + а1 • 1041521 1169 = 7675449462

Делим каждое уравнение на коэффициенты при ao и получаем:

а_о + 50950 а1 = 37150

а₀ + 51100 а1= 37660

Путем вычитания из второго уравнения первого получаем:

150а1 = 510: а1 = 3,4

.Подставляя значение а1 в первое уравнение получаем:

Ао+50950 -3,4 = 37150:а₀= -136,080

Уравнение регрессии примет вид:

Ух=136,080 + 3,4х

Проверка указана в последней графе табл.4.2.

Соответствующие расчеты выполнены для всех больниц Лены и имеют следующие результаты коэффициента корреляции, свидетельствующего о тесноте связи между признаками, т.е. о степени адекватности предполагаемой регрессионной модели процессу, который она описывает: ЛЦЕБ-0,69; Нижнеянская-0,77; Пеледуйская-0,3; Алексеевская - 0,98; Киренская-0,32; Осетровская - 0,71.

Линейный коэффициент корреляции изменяется, при прямой свя­зи, от 0 до 1, а она такова, что было доказано построением графиков на корреляционных полях. Чем теснее связь между признаками, тем ближе к единице будет значение коэффициента корреляции. Для качественной оценки тесноты связи используется таблица Чеддока, в соответствии с которой для ЛЦББ, Нижнеянской и Осетровской больниц - связь оцени­вается как высокая. Для Алексеевской - как весьма высокая, а для Пеледуйской и Киренской больниц - как умеренная. О чем это говорит, о том, что результаты плановых и прогнозных расчетов будут менее точ­ны для двух последних больниц.

Уравнения регрессии для линейных больниц:

Для Нижнеянской линейной больницы - Ух= 2100 + 0,366Х;

Пеледуйской линейной больницы - Ух = 680 + 0,012Х;

Алексеевской - Ух = -1070 + 0,142Х;

Киренской линейной больницы - У_х = -278 + 0,043Х;

Осетровской линейной больницы – Ух = - 970 + 0,06Х

Таким образом, используя полученные модели, можно достаточно быстро просчитать различные прогнозные варианты затрат по заработ­ной плате в зависимости от различных вариантов объема медицинских услуг по каждой больнице.