Образец типового расчета

Задача 1. Используя градиентный метод, найти минимум функции при системе ограничений .

Решение

Строим область допустимых решений, вектор и одну из линий уровня . Перемещаем линию уровня в направлении, противоположном , так как решается задача на отыскание минимума функции. Опорная прямая проходит в этом случае через точку А, координаты которой найдём из решения системы

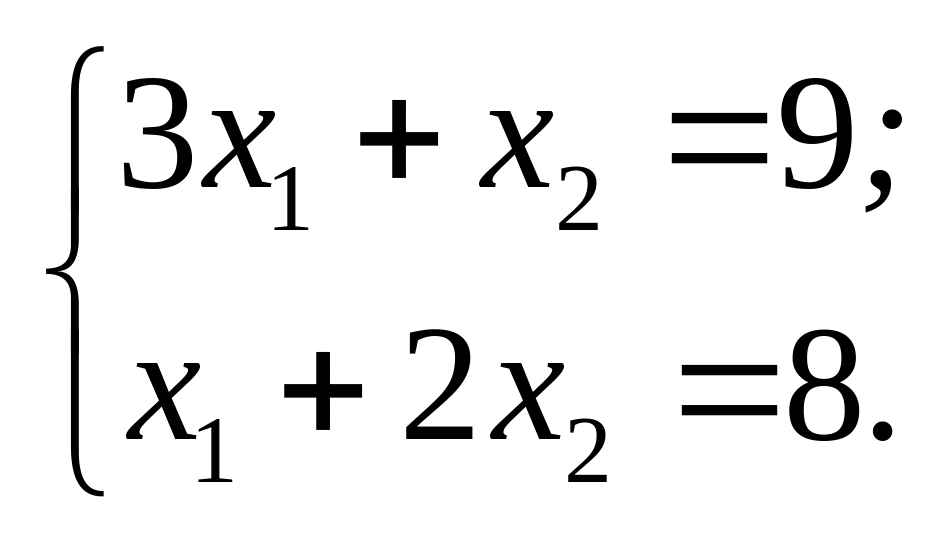
Итак, . Вычисляем .

Замечание. В действительности от вида области допустимых решений и целевой функции задача ЛП может иметь единственное решение, бесконечное множество решений или не иметь ни одного решения.

Задача 2. Составить математическую модель и решить симплекс-методом следующую задачу.

Строительное управление ведет капитальный ремонт жилых домов. Перегородки внутри этих домов могут быть изготовлены гипсобетонными или каркасными. Ресурсы на месяц заданы в табл. 7.7 (потребность на 1 м² площади перегородок).

Таблица 7.7

Н аименование	Каркасные	Гипсобетонные
Гипсобетон	–	0,25 м3
Пиломатериалы	0,08 м3	0,1 м3
Сухая штукатурка	4 м3	–
Трудоресурсы	0,8 чел. дн.	0,5 чел. дней

Рассчитать общее количество м² как каркасных, так и гипсобетонных перегородок, которые следует возвести в текущем месяце, чтобы общая их площадь была наибольшей, если строительное управление имеет в наличии гипсобетона – 300 м³; пиломатериалов – 200 м³; сухой штукатурки – 8000 м³; трудоресурсов – 2000 чел/дней.

Решение

Составим математическую модель задачи. Пусть требуется возвести каркасных и гипсобетонных перегородок. Из условия на это уйдёт: гипсобетона , пиломатериалов , сухой штукатурки , трудоресурсов . Учитывая лимиты материалов и трудоресурсов, составляем систему ограничений – неравенств:

Для решения задачи симплекс-методом вводим дополнительные переменные:

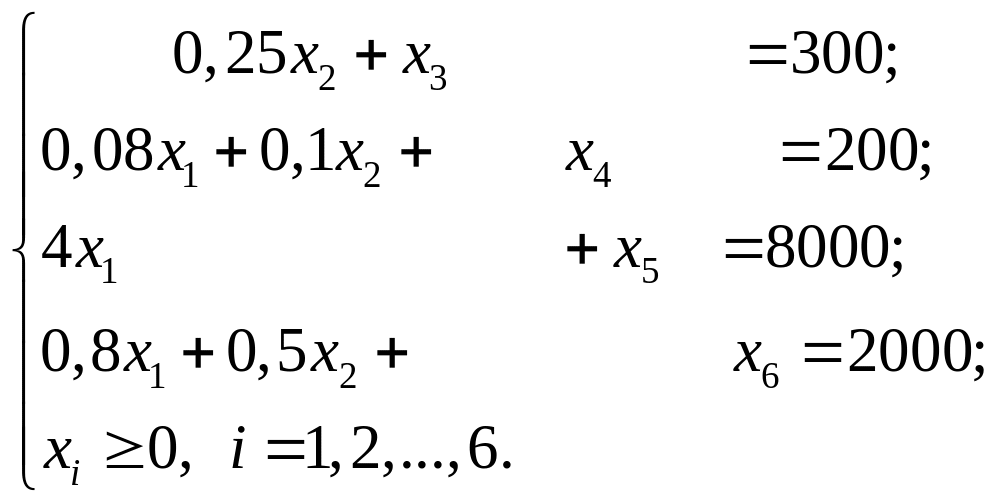
Полагаем . Принимаем , в качестве свободных переменных, , , , в качестве базисных. Начальный опорный план имеет вид: , . Составляем симплекс-таблицу (в сокращённой форме), соответствующую начальному опорному плану. Обратим внимание, что коэффициенты при свободных переменных пишутся с противоположным знаком.

- - 0 0,25 300 0,08 0,1 200 1 0 2000 0,8 0,5 2000 1 1 0

Выбираем какой-либо положительный элемент в последней строке симплекс-таблицы ( среди коэффициентов при и в целевой функции) и соответствующий столбец объявляем ведущим. Например, объявим ведущим второй столбец и поставим стрелку вверх. Подсчитаем отношения свободных членов к положительным элементам ведущего

столбца:

, , .

Элемент ведущего столбца, для которого отношение минимально ( в нашем случае 0,25) объявляем ведущим. Строка, в которой находится элемент, также называется ведущей и помечается стрелкой слева.

Теперь запишем правила перехода к новой симплекс-таблице, соответствующие приведённому выше алгоритму симплекс-метода:

1. Базисная переменная, находящаяся в ведущей строке, и свободная переменная, находящаяся в ведущем столбце, меняются местами.

2. Ведущий элемент заменяется величиной, ему обратной.

3. Все элементы ведущей строки (включая свободный член), кроме ведущего элемента, заменяются их отношениями к ведущему элементу.

4. Все элементы ведущего столбца (кроме ведущего элемента) заменяются взятыми с обратными знаками их отношениями к ведущему элементу.

5. Остальные элементы заменяются по «правилу 4 элементов»: любой такой элемент умножается на ведущий и из произведения вычитается произведение двух других элементов, составляющих с первыми вершины прямоугольника, после чего результат делится на ведущий элемент.

Проводя вычисление по этим правилам, получаем следующую симплекс-таблицу:

- - 0 4 1200 0,08 -0,4 80 1 0 2000 0,8 -2 1400 1 -4 -1200

Значение -1200 ещё не является минимальным для функции , т.к. в последней строке ещё есть положительный коэффициент.

Аналогично составляем следующую симплекс-таблицу:

- - 0 4 1200 12,5 -5 1000 -12,5 5 1000 -10 2 600 -12,5 1 -2200	Значение -2200 не является минимальным для . Составим ещё одну симплекс-таблицу:
- - 400 2000 -10 -1/5 -2400	Пересчитывая последнюю строку, сразу убеждаемся, что значение -2400 является минимальным для функции . Нам ещё следует пересчитать свободные члены при и . Поскольку в опорном плане, соответствующем симплекс-таблице, свободные неизвестные равны 0, то найденные значения свободных членов при и дадут оптимальный план производства:

,

.

Задача 3. Максимизировать функцию Z=x₁+2x₂-2x₃ при ограничениях

Решение

Преобразуем исходную задачу линейного программирования к канонической. Для этого введём в ограничения дополнительные неотрицательные переменные. А именно, в первое неравенство – переменную x₄ со знаком «+», во второе – x₅ со знаком «-». Система ограничений примет вид:

Эту систему запишем в векторной форме: A₁x₁+A₂x₂+A₃x₃+A₄x₄+A₅x₅=B, где , , , , , .

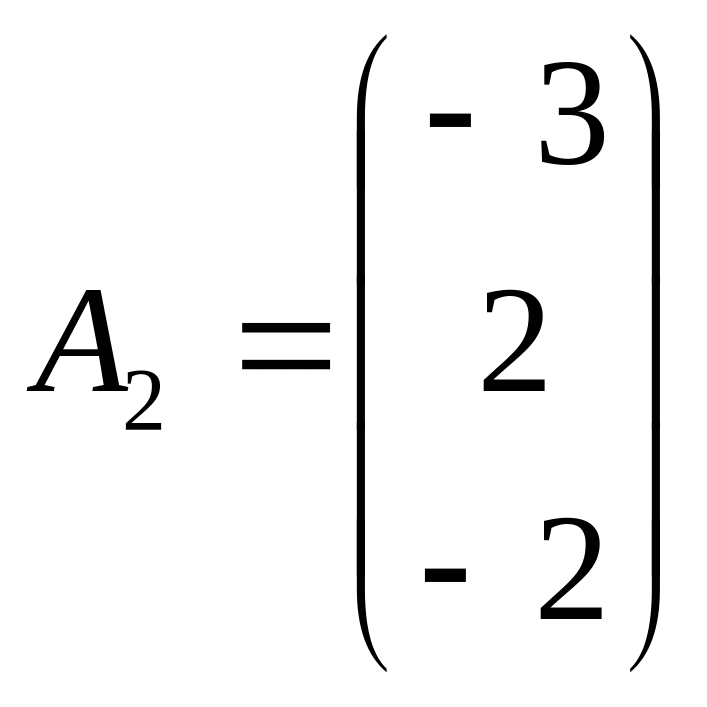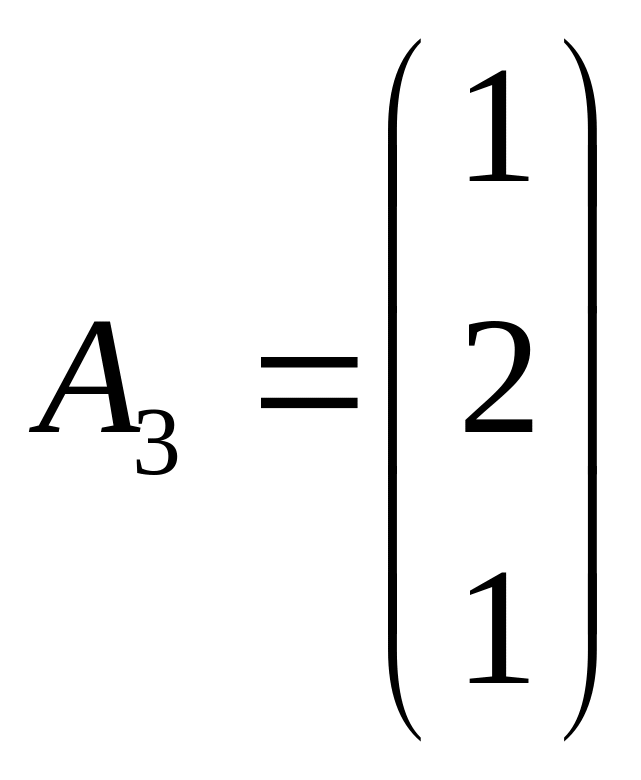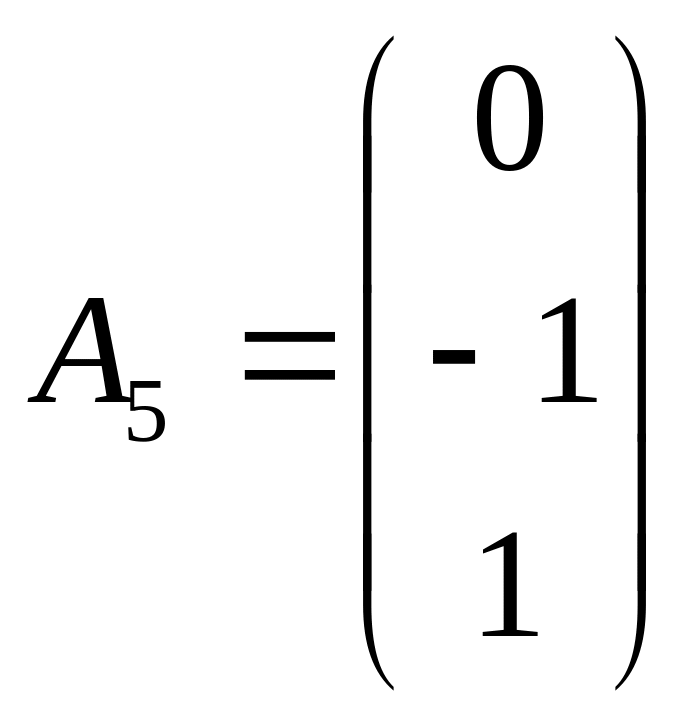Очевидно, что в данной системе ограничений отсутствует единичный базис. Это означает, что среди векторов A_j нет трёх необходимых единичных векторов, которые должны образовывать базис в R³. Однако заметим, что вектор A₄ является частью базиса. Ему соответствует базисная переменная x₄. Необходимо найти ещё два единичных вектора. Для этого применим метод искусственного базиса. Введём искусственные переменные в те уравнения ограничений, в которых не присутствует базисная переменная x₄, и построим следующую вспомогательную задачу (ВЗ):

F=-w₁-w₂max

где w₁, w₂ – искусственные переменные. Система ограничений ВЗ в векторном виде имеет вид: A₁x₁+A₂x₂+A₃x₃+A₄x₄+A₅x₅+A₆w₁+A₇w₂=B, где векторы A_j , j=1,2,3,4,5 определяются так же, как и выше, а и . Таким образом, вектора A₄, A₆, A₇ образуют базис в R³ и им соответствуют базисные переменные (БП) – x₄, w₁, w₂. Все остальные переменные, а именно x₁, x₂, x₃, x₅ объявляются свободными (СП). Далее к ВЗ применяем обычный симплекс-метод. Как и раньше (см. § 5. 1) начальный опорный план получается, если присвоить свободным переменным значения, равные нулю. При этом базисные переменные принимают значения, равные числам в соответствующей строке столбца свободных коэффициентов В, то есть x₁=x₂=x₃=x₅=0¸ а x₄=8, w₁=4, w₂=12. Строим симплекс-таблицу, соответствующую начальному опорному плану:

СП БП	x1	x2	x3	x5	B
x4	2	-3	1	0	8
w1	1	2	2	-1	4
w2	3	-2	1	1	12
F	-4	0	-3	0	-16

С этой таблицей проводим необходимые преобразования (см. §5.1) симплекс-метода, пока не получим оптимальную симплекс-таблицу или не получим неразрешимость. В нашем случае, мы уже на втором шаге будем иметь такую симплекс-таблицу:

СП БП	w1	x2	x3	w2	B
x4	-0,5	-3	-0,5	-0,5	0
x1	0,25	0	0,75	0,25	4
x5	-0,75	-2	1	1	0
F	1	0	0	1	0

Эта таблица будет оптимальной для ВЗ. При этом все искусственные переменные стали свободными и max F=0. Вычеркивая столбцы, соответствующие искусственным переменным и последнюю строку, и приписывая новую строку оценок с использованием исходной целевой функции Z(X), получим начальную симплекс-таблицу для исходной задачи ЛП:

СП БП	x2	x3	B
x4	-3	-0,5	0
x1	0	0,75	4
x5	-2	1	0
Z	-2	2,75	0

Проанализировав последнюю таблицу, делаем вывод, что исходная задача ЛП не имеет решения в силу неограниченности целевой функции.

Задача 4. Для данной задачи составить двойственную, решить ее графическим методом и, используя вторую теорему двойственности, найти решение исходной задачи:

, .

Решение приведено на стр. 6 – 7 данной методички.

Задача 5. Решить транспортную задачу (табл. 7.8).

Таблица 7.8

Поставщики	Потребители										Запасы
	В1		В2		В3		В4		В5
А1		10		7		4		1		5	100
А2		2		7		10		6		11	250
А3		8		5		3		2		2	200
А4		11		8		12		16		13	300
Запросы	200		200		100		100		250		850

Решение приведено на стр. 13 – 17 данной методички.