
§1. Топология прямой

 дополнение
множества А.
дополнение
множества А.
 –
множество индексов.
–
множество индексов.
 окрестность А
окрестность А
 ⋃
⋃
Определение
1.
Множество А называется открытым, если

Определение 2. Множество А называется замкнутым, если его дополнение открыто.
Свойства:
 открытые
множества. Тогда их объединение (всех),
множество
открытые
множества. Тогда их объединение (всех),
множество
 ,
открыто.
Доказательство:
Рассмотрим
,
открыто.
Доказательство:
Рассмотрим
 ,
элемент
.
Тогда
,
элемент
.
Тогда
 .
. открыто.
Тогда
открыто.
Тогда
 т.к.
т.к. .
Т.к.
.
Т.к.
 ,
то
,
то
 ,
ч.т.д.
,
ч.т.д. открытые
множества. Тогда их пересечение (всех),
множество
открыто.
Доказательство:
Рассмотрим
,
элемент В. Тогда
открытые
множества. Тогда их пересечение (всех),
множество
открыто.
Доказательство:
Рассмотрим
,
элемент В. Тогда
 .
откытое
множество. Тогда
.
откытое
множество. Тогда
 т.к.
.
Пусть
т.к.
.
Пусть
 ,
он существует т.к. множеств конечное
число и положителен, т.к.
,
он существует т.к. множеств конечное
число и положителен, т.к. .
Тогда
.
Тогда
 .
Тогда
.
Тогда
 ,
ч.т.д.
Замечание.
Это свойство не верно для бесконечного
числа множеств, например
,
ч.т.д.
Замечание.
Это свойство не верно для бесконечного
числа множеств, например
 .
Тогда пересечение этих, очевидно
открытых, множеств:
.
Тогда пересечение этих, очевидно
открытых, множеств:
 ,
не является открытым множеством.
,
не является открытым множеством.
Определение
3.
 называется граничной точкой множества
называется граничной точкой множества ,
,
 множество
всех таких точек А.
множество
всех таких точек А.
Замечание.
Очевидно, что
 ,
т.к.
,
т.к.

Теорема.
 открыто
открыто
 Доказательство:
Доказательство:
(⇒) Пусть
 и
и
 ,
?!
,
?!(⇐) Пусть не открытое множество. Тогда
 .
Но
.
Но
 .
Тогда по определению
граничная точка
.
Тогда
.
Тогда по определению
граничная точка
.
Тогда
 (?!).
(?!).
Следствие.
замкнуто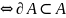 .
Доказательство:
замкнуто
.
Доказательство:
замкнуто открыто
открыто

Определение
4.
 внутренняя
точка множества
,
если
внутренняя
точка множества
,
если
 .
Множество всех таких точек для этого
множества обозначается
.
Множество всех таких точек для этого
множества обозначается .
Очевидно, что
.
Очевидно, что
 .
.
Определение
5.
Замыканием множества А называется
множество
 ,
обозначаемое
,
обозначаемое

Утверждение.
открытое, более того, если
открытое и
 ,
то
,
то
 .
Доказательство:
Заметим,
что
.
Доказательство:
Заметим,
что
 .
Пусть
.
Пусть
 и
и
 .
. ⇒
⇒
 .
Тогда
не открыто (?!).
Пусть
.
Тогда
не открыто (?!).
Пусть
 и
и
 .
Но
.
Но
 и
и
 (?!).
(?!).
Следствие.
 замкнутое, более того, если
замкнутое и
замкнутое, более того, если
замкнутое и
 ,
то
,
то
 .
Доказательство:
1)
Заметим, что
.
Доказательство:
1)
Заметим, что
 Т.к.
Т.к. открытое по доказанному, то
замкнутое по определению.
2)Раз
замкнутое, то его дополнение открытое.
Тогда по п.1) и доказанному утверждению:
открытое по доказанному, то
замкнутое по определению.
2)Раз
замкнутое, то его дополнение открытое.
Тогда по п.1) и доказанному утверждению:
 ,
что и требовалось доказать.
,
что и требовалось доказать.
§2. Супремум и инфимум
Определение
1.
– верхняя грань множества
если
 .
.
Определение
2.
– нижняя грань множества
если
 .
.
Определение
3.
Верхняя грань
 множества
называется супремумом
множества
,
если
множества
называется супремумом
множества
,
если
 – верхней грани множества
– верхней грани множества
 .
.
Обозначение.
Супремум множества
обозначается
 .
.
Определение
4.
Нижняя грань
 множества
называется инфимумом
множества
,
если
– нижней грани множества
множества
называется инфимумом
множества
,
если
– нижней грани множества
 .
.
Обозначение.
Инфимум множества
обозначается
 .
.
Аксиома(верхней грани). Если у множества существует верхняя грань, то существует и супремум.
Теорема.
Если у множества
существует
нижняя грань, то существует и инфимум.
Доказательство:
Рассмотрим
множество
 ,
состоящее из элементов, противоположных
соответствующим элементам множества
.
Заметим, что у этого множества существует
верхняя грань, противоположная верхней
грани множества
.
Тогда по аксиоме верхней грани у него
есть супремум. Очевидно, что число,
противоположное этому супремуму будет
являться инфинумом множества
.
Теорема доказана.
,
состоящее из элементов, противоположных
соответствующим элементам множества
.
Заметим, что у этого множества существует
верхняя грань, противоположная верхней
грани множества
.
Тогда по аксиоме верхней грани у него
есть супремум. Очевидно, что число,
противоположное этому супремуму будет
являться инфинумом множества
.
Теорема доказана.
Замечание.
 ,
,
 .
.
Теорема(Кантора
о вложенных отрезках).
Пусть
 – система вложенных отрезков, то есть
– система вложенных отрезков, то есть
 .
Тогда
.
Тогда
 .
Доказательство:
Рассмотрим
множество
.
Доказательство:
Рассмотрим
множество
 .
Тогда
.
Тогда
 подходит. Действительно,
подходит. Действительно,
 .
Первое неравенство верно потому, что
.
Первое неравенство верно потому, что
 – это верхняя грань
,
а второе потому, что
– это наименьшая из верхних граней и
– это верхняя грань
,
а второе потому, что
– это наименьшая из верхних граней и
 – это верхняя грань
.
Теорема доказана.
– это верхняя грань
.
Теорема доказана.
