Задача 1.3.6

В каких температурных интервалах средняя теплоемкость С_р(Т₁, Т₂) на примереNa₂Si₂O_5.

Решение.

В соответствии с (1.8)

,

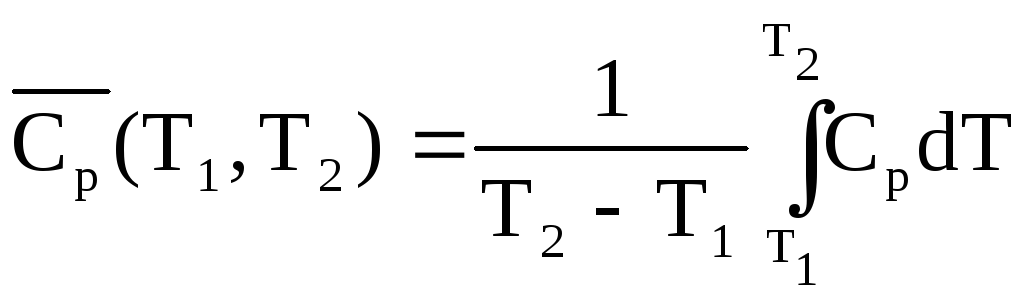где С_р =a+bT+c/T²

После интегрирования и элементарных преобразований получим:

Коэффициенты уравнения С_р=F(T):

Вещество	Коэффициенты уравнения Ср =F(T),Дж/моль К				Температурный интервал, К
	Ср298	a	b x 103	c x 10-5
 - Na2Si2O5 (тв)	156,5	185,69	70,54	- 44,64	298-951
 - Na2Si2O5 (тв)	—	292,88	—	—	951-1147
Na2Si2O5 (жидк)	—	261,21	—	—	1147-2000

Анализ приведенных уравнений показывает, что требуемое условие будет соблюдаться в том случае, когда истинная теплоемкость не зависит от температуры (Тривиальный случай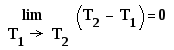не рассматривается).

В нашем случае это условие соблюдается в области температур существования (тв) 951-1147 К где Дж/ и в области существования (жидк) 1147-2000 К, но где Дж/.

Задача 1.37

Определите объемную и удельную плотности аккумулируемой тепловой энергии при нагревании воды от 0 до . Обсудите недостатки такого способа аккумулирования тепла.

Решение.

При нагревании веществ от температуры дозатрачивается, а, следовательно, аккумулируется теплота, которая может быть рассчитана по уравнению:

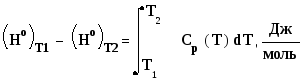
где 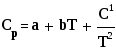, и для жидкой воды в интервале температур 273-373К [i].

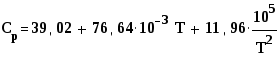
Тогда:

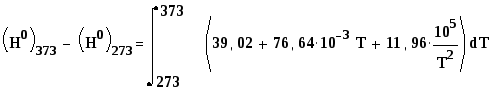
И

Считая плотность жидкой воды кг/, определим число молей в 1 как моль/. Тогда объемная плотность аккумулируемой тепловой энергии равна:

И, подставив полученные значения:

Удельная плотность аккумулированной тепловой энергии [Кдж/кг] будет собственно равна Кдж/кг. Сравним полученный результат с результатом на основе среднего значения теплоемкости .

Рассчитаем вначале среднее значение теплоемкости жидкой в исследуемом интервале температур:(1.)

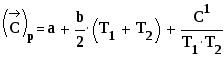
Подставляя значения коэффициентов уравнения , получим:

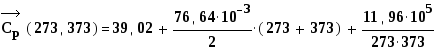
и Дж/

Тогда Кдж/моль

и Мдж/ ;

Различие между точным и приближенным решением не превышает 1%. Недостатком такого способа аккумулирования является отсутствие возможности использовать преимущества теплоснабжения при постоянной температуре.

Задача 1.38

Известен экологически чистый способ теплового аккумулирования, основанный на использовании теплоты фазового перехода плавление-кристаллизация. Во время плавления температура вещества остается постоянной до расплавления всей массы вещества.

При охлаждении имеет место обратный процесс – кристаллизация с выделением аккумулируемой теплоты.

Обычно процесс проводят в области температур таких, что К, что обеспечивает постоянство температуры при отборе аккумулируемой теплоты.

Рассчитайте удельную и объемную 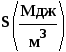плотности аккумулированной тепловой энергии в интервале температур - , для гексагидрата нитрата никеля и додекагидрата сульфата аллюминия-аммония . Необходимые для расчета данные приведены в таблице.

Вещество	(С)
	56,7	152,3	2,65	1,77	1,98	1,99
	93	250,6	1,65	1,28	1,55	3,05

Решение.

Отметим прежде всего, что до 120С теряет 5 молекул и при 200С 6 молекул, а разлагается при Т>140С. Поэтому в исследуемом интервале температур химические превращения отсутствуют.

Поскольку интервал температур достаточно мал, то можно использовать среднее значение теплоемкостей и плотностей. Тогда согласно (1.12) удельная плотность аккумулированной энергии:

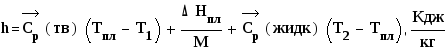
И объемная плотность аккумулированной энергии:

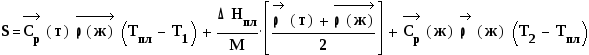
В условии имеются все необходимые для расчета данные. Результаты расчета:

Вещество	(С)
	56,7	5	172,1	380,0
		10	192	423,6
	93	5	273,6	399,4
		10	296,1	431,6

Анализ полученных результатов приводит к выводу, что, во-первых, рассматриваемый способ аккумулирования дает возможность проводить отбор тепловой энергии при практически постоянной температуре (поскольку при кристаллизации температура остается постоянной), во-вторых, варьировать эту температуру за счет подбора соединения с температурой плавления в необходимом температурном интервале, и, наконец, в-третьих – удельная и объемная плотности аккумулированной энергии соизмеримы с таковыми при использовании внутреней энергии горячей воды с изменением температуры около 80-100С.

Задача 1.3.9

Рассмотрите возможность использования в качестве аккумулятора тепловой энергии.

Решение.

Приведем прежде всего данные [1], необходимые для анализа и расчетов.

Вещество	Коэффициенты уравнения		Температурный интервал
	a		Т, К	Т, С
	83,32	154,36	298-522	25-249
	145,05	54,60	522-980	249-707
	142,68	59,31	980-1157	707-884
	19,74	--	1157-2000	884-1727

Анализ приведенных данных показывает, что в зависимости от температуры, при которой отбирается теплота от аккумулятора, использование возможно или в температурном интервале , с использованием теплоты перехода или в температурном интервале , с использованием теплоты плавления.

Критерием возможности использования может служить количество аккумулированной энергии, т.е. удельная и/или объемная 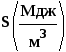плотности энергии.

Тогда:

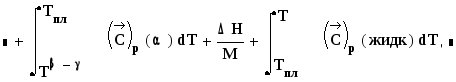
Где - удельная теплоемкость, Кдж/кг; М – молярная масса вещества.

Температурная зависимость удельной теплоемкости с учетом величины кг/моль:

Тогда

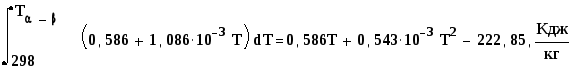
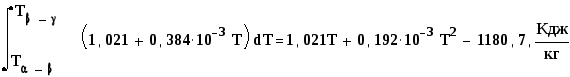
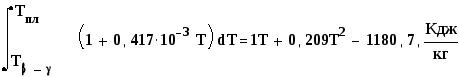
Результаты расчетов оформим в виде таблицы. Значения объемной плотности энергии рассчитаны по соотношению , где –плотность .

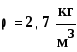Т, К
348	75	6,6	-	-
373	100	10,0	70,4	190,2
473	200	25,0	176,0	475,8
522	249	32,8	231,2	624,9
522	249		307,3	830,5
673	400	70,5	-	-
873	600	107.9	-	-
980	707	128,85	-	-
980	707		909,4	-
1100	827	153,6	1081,3	2922,4
1157	884	165,6	-	-
1157	884		1327,7	3588,4