Задача 3.3.13

Проследите влияние температуры на степень превращения

оксида углерода при стехиометрическом соотношении

CO:H₂O(газ) в реакции конверсии оксида углерода водяным

паром:

CO + H₂ O (газ)  CO₂ +H₂

Рассчитайте состав газовой смеси при равновесии в зависимости

от температуры.

Решение.

CO + H₂O (газ)CO₂ + H₂

Исходный 1 1 0 0

Состав, моль

Равновесный 1- 1-    ,

Состав

где - химическая переменная (3,43)

Тогда константа равновесия К_a в соответствии с(3,46),поскольку

=0 :

откуда

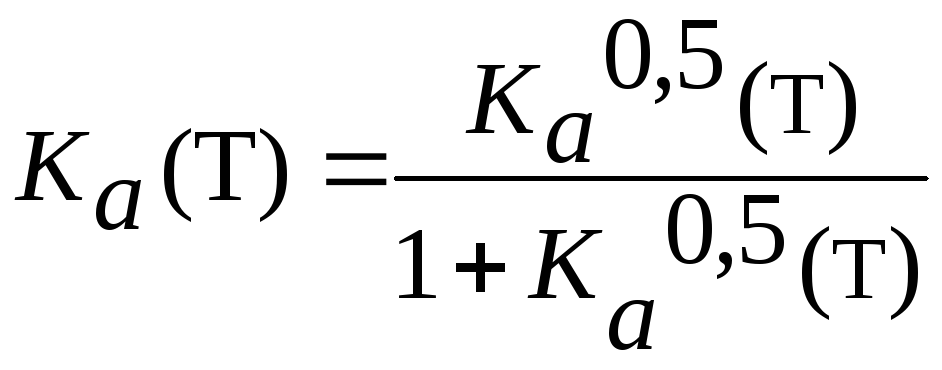
Учтя (3,47),получим значение степени превращения CO

_со = (т.к. n₀ (co) =1)

После подстановки значений Ка (т) при различных температурах получим

Т	298	500	600	700	800	900	1000
Кa	10482,0	137,00	28,20	9,39	4,22	2,29	0,70
ХСО	0,99	0,92	0,84	0,75	0,67	0,60	0,45

При низких температурах степень превращения очень велика (что подтверждает выводы предыдущей задачи), однако скорость процесса при таких температурах незначительна.Низкотемпературный цинкхроммедный катализатор,используемый в промышленности, обеспечивает необходимую скорость процесса при температуре 350°-400°(600-700К).При этих температурах степень превращения Х_СО остается

достаточно высокой.Проследите влияние соотношения пар: газ(H₂O:CO) на степень превращения оксида углерода в реакции конверсии оксида у углерода водяным паром при Т=800К.

Решение:

Состав,моль. СО+H₂O(газ)→CO₂+H₂

Исходный 1 n 0 0

Равновесный 1- n-  

где - химическая переменная (3,34)

Тогда константу равновесия К_a можно представить (3,46) как:

И при Т=800К (значения К_a(т) рассчитаны в задаче 3.3.13):

Для исследуемой реакции- степень превращения СО=  (3,47),

поскольку n_o(Co)=1

Равновесный состав (в мольных долях NC) может быть

выражен следующими соотношениями:

;;

Рассчитаем Х_СО и N_i при значениях n=1;2;3;4.

Соотношение Пар: газ =n :1	Степень превращения χCO	Равновесный состав
		NCO
1	0,67	0,165	0,165	0,335	0,335
2	0,85	0,05	0,38	0,28	0,28
3	0,90	0,025	0,525	0,225	0,225
4	0,93	0,014	0,614	0,186	0,186

Результаты показывают ,что при увеличении соотношения пар:газ до 4:1 степень превращения χ_co увеличивается от 0,67 до 0,93.

Этими соображениями руководствуются при проведении исследуемого процесса в промышленности :соотношение пар:газ обычно поддерживается как 4:1 .Результаты показывают так же , что соотношение между исходными веществами влияет на равновесный выход продуктов : максимальный выход получают при стехиометрическом соотношении исходных веществ . Таким образом ,для максимального выхода продуктов реакции необходим стехиометрический состав исходных веществ ,а для достижения

Максимальной степени превращения – избыток.

Задача 3.3.15.

В водородном генераторе при температуре 800 К и давлении Р=1атм. Протекает реакция CO+H₂O(газ)  CO₂+H₂

Считая , что в генераторе достигаются равновесные концентрации

, определите возможность образования сажи (углерода) при этих условиях.

Решение.

Образование углерода возможно ,если при данных условиях возможен самопроизвольный процесс:

2CO  CO₂+C (тв)

критерием самопроизвольного протекания процесса в соответствии

с(3.39) и (3.40) является условие

Δ_rG(T)< 0,

потеря соблюдается,если

П_i P^νi_Ai<K_a(T) (3.40)

Для рассматриваемой реакции это условие конкретизуется

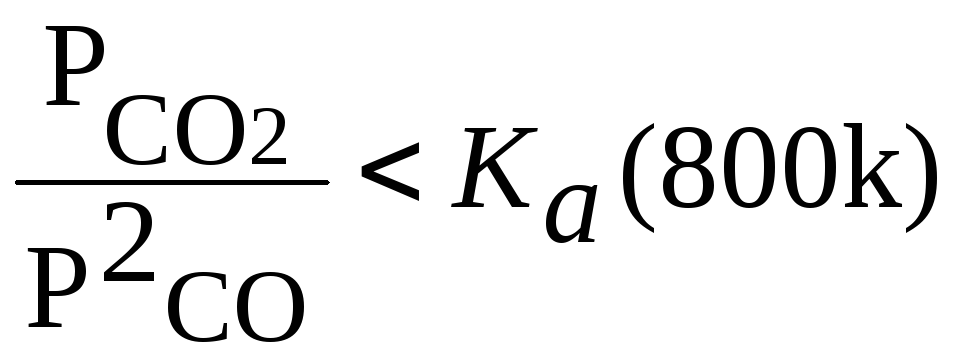
Равновесные парциальные давления P_CO2=N_CO2 P и P_CO=N_CO P при 800К и различном соотношении пар:газ возьмем из предыдущей задачи.

Константу активности К_а при 800К (отметим попутно, что в

данном случае K_a= K_p, поскольку общее давление в системе

Р=1атм.) рассчитаем через Константы активности образования

К_f[1] исходных веществ и продуктов реакции():

2CO→Co₂.+ С (тв)

lg K_f(800K) (11,86 25,80 0) =lg K_a(800)=2,08;

K_a (800)=120,2 тогда при соотношениях пар: газ_: n_CO

(a): 1:1;

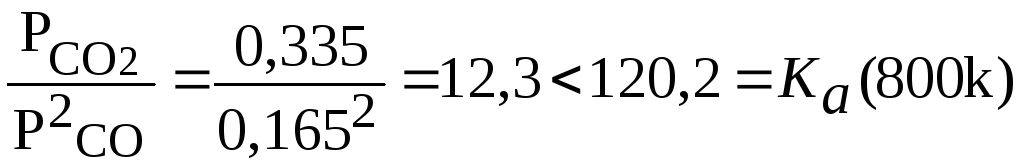
2:1;

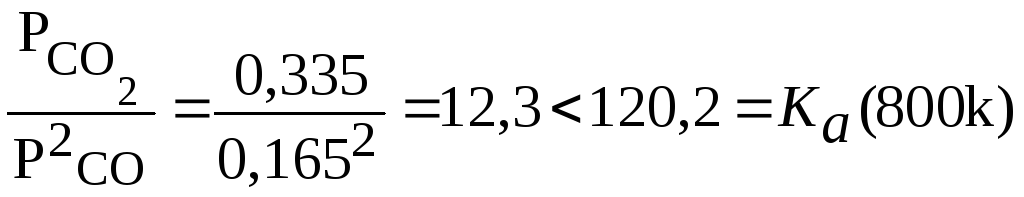
3:1;

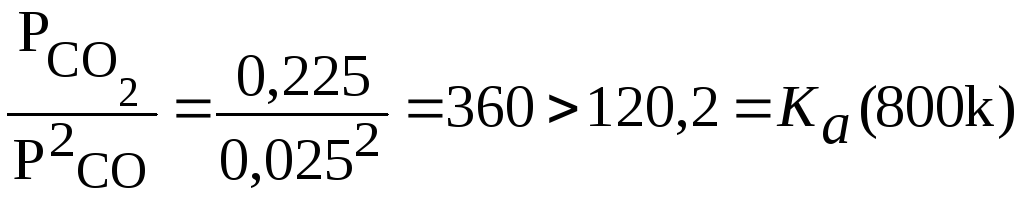
4:1;

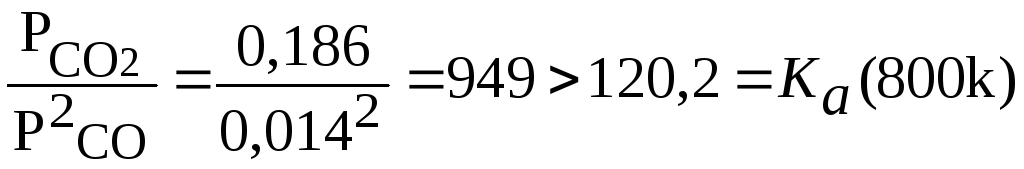
Следовательно, при соотношение-пар: газ как 3:1 и 4:1 при 800К выпадение сажи не возможно.

Задача 3.3.16

В водородном генераторе при 800К и общем давлением Р=1атм протекают процессы

CO+H₂O (газ)→ СО₂ + H₂ (1)

2CO→ CO₂ + C (тв) (2)

Решение определите состав системы при равновесия.Рассматриваемая, задача достаточна, типична: в химических системах могут протекать сложные процессы,включающие множество взаимодействий с одним или несколькими исходными или промежуточными веществами.Принцип расчета равновесий в сложных системах заключается в следующем;(a)-зная начальный состав выражают равновесный состав с учетом всех возможных в системе превращений (каждая реакция характеризуется своей химической переменной ξ ). Для процесса , состоящего из нескольких реакций , активности(или концентрации) реагирующих веществ должны одновременно удовлетворять всем равновесиям.

CO+ H₂O(газ)  CO₂ + H₂ (1)

Исходный 1 1 0 0

Состав,моль

Равновесный 1-ξ₁-2ξ₂ 1-ξ₁ ξ₁+ξ₂ ξ₂

Состав,моль

2CO  CO₂ +C (тв) (2)

исходный

состав, моль 1 0

равновесный 1-ξ₁-2ξ₂ ξ₁+ξ₂

состав , моль

(б)- записывают выражение, связывающие константы равновесия К_a с составом (3.42) для каждой реакции. Число таких уравнений

равно числу рассматриваемых реакций. Тогда для реакции (1) и (2)

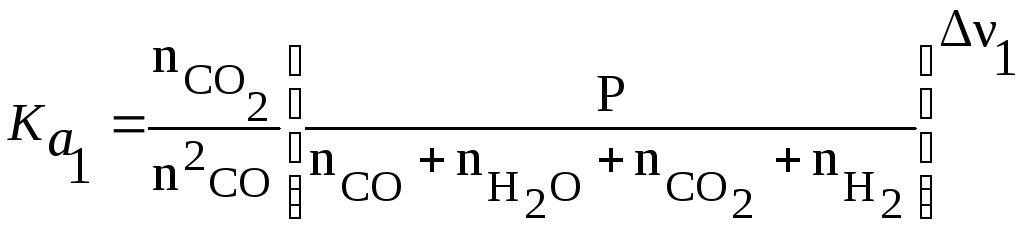
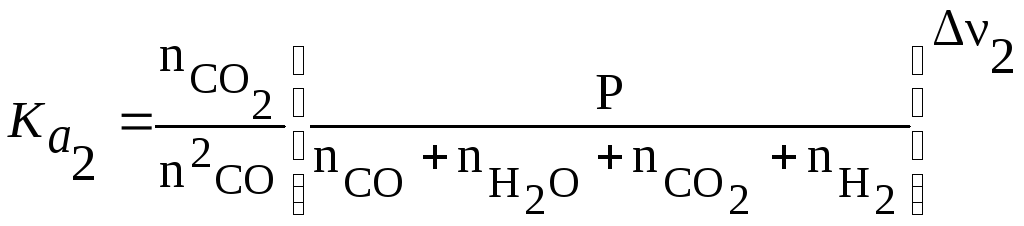
Учтя ,что ν₁=0,  ν ₂=-1 и Р=1атм,после подстановки значений

и:

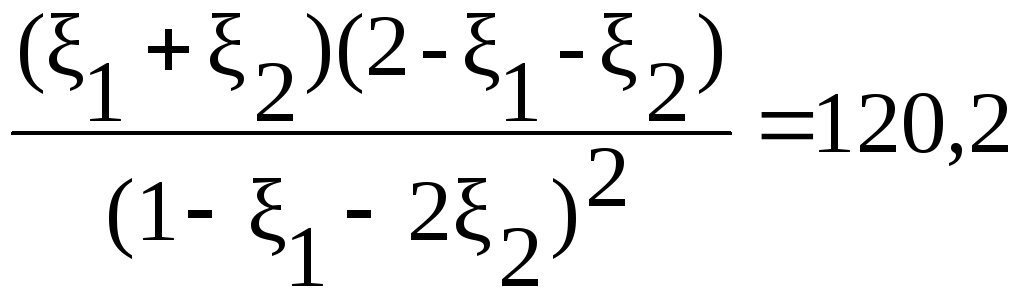
(в)- решение системы S нелинейных уравнений, где S-число

рассматриваемых реакций. Решение системы нелинейных уравнений представляет довольно не простую задачу, однако, применение современных программных средств, например, Match-Cad, позволяет решать такие задачи. Более того, такие задачи могут быть решены с использованием программируемые микрокалькулятором [7].Однако ведь может так случиться, что ни ПЭВМ, ни ПМК нет под рукой (вообще-то они, конечно, есть; ведь у нас у каждого студента, ассистента, доцента и т.д. все это есть, но просто нет

под рукой!)

Тогда можно использовать простой и наглядный метод, который

называют методом релаксации или методом последовательно

соединенных реакторов.

Отступление третье, в котором рассказывается о методе релаксация, или методе последовательно соединенных растворов.

Рассматриваемую совокупность реакций представляют в виде

Системы последовательно соединенных растворов, число которых

равно числу независимых стехиометрических уравнений.

Каждый раствор R_i; действует как периодический, в котором

достигается равновесия в I-ой реакции, т.е. в реакции, номер

Которой соответствует номеру раствора.

Процесс начинают с загрузки(конечно, мысленно !) в исходный реактор R₁.Полученные продукты перегружают во второй реактор R₂, в котором достигает равновесия второй реакции.

Затем продукты перегружают в третий реактор R₃ и так далее.

В каждый реактор поступает равновесная смесь продуктов из предыдущего ректора и в каждом реакторе R_i протекает только одна i-ая реакция.

Первый проход заканчивается после того, как смесь прошла реактор, номер которого соответствует номеру реакции n.

После последнего реактора R_n полученную реакционную смесь загружают в первый реактор и цикл повторяется до тех пор, пока степень протекания каждой реакции не станет меньше НЕКОТОРОЙ наперед заданной величины.

Сказанное поясняет рисунок.

R₁ R₂ R_n

Рис. Рецикл равновесного потока

Из сказанного следует, что метод последовательно соединенных реакторов позволяет вместо системы из n нелинейных уравнений решать nk нелинейных уравнений с одной неизвестной (k-число “проходов”, или рециклов)

В каждом новом “проходе” системы реакторов степень превращения постепенно снижается, достигая некоторую наперед заданную величину.

Число “проходов” заранее предсказать трудно.

Теперь вернемся к задаче 3.3.16, которую будем решать, используя метод последовательно соединенных реакторов. Число “проходов” j ограничим значением ξ=0,003.

Пусть исходный состав смеси на входе в i-ый реактор

ξ n_co, .

Тогда равновесный состав для реакции

CO + H₂O CO + H₂ (1)

Равновесный n_CO-x_ij n_H2O -x_ij n_CO2+x_ij n_H2+x_ij

состав, моль

где x_ij – химическая переменная в i-ом реакторе после j-го “прохода” R_ij, i=1;2

И константа равновесия K_a связана с равновесным составом:

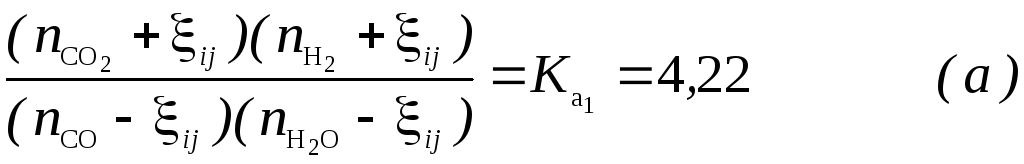
Для реакции

(2)

равновесный

состав, моль

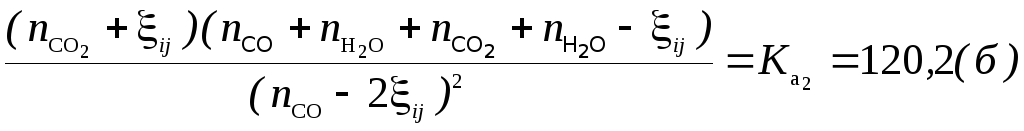
Последовательность, этапы и результаты расчета показаны на схеме, в которой R_ij и ξ_ij соответственно i-ый реактор R_i и значение химической переменной в i-ом реакторе после j-го «прохода». (i=1; 2 число реакторов, равное числу рассматриваемых реакций).

Каждое уравнение (а) и (б) решали с использованием приближенных методов(см. отступление второе)

Вход R₁₁

	CO	H2O	CO2	Н2
n	1	1	0	0
N	0,5	0,5	0	0
ån=2

R₁₁

выход R₁₁ входR₂₁

CO+H2O CO2+H2

	CO	H2O	CO2	Н2
n	0,328	0,328	0,672	0,672
N	0,164	0,164	0,336	0,336
ån=2

ξ₁₁=0,672

R₂₁

2CO CO2+C(тв)

выход R₂₁ вход R₁₂

	CO	H2O	CO2	Н2
n	0,108	0,328	0,782	0,672
N	0,057	0,174	0,414	0,355
ån=1,89

ξ₂₁=0,11

выходR₁₂ входR₂₂

R₁₂

CO+H2O CO2+H2

	CO	H2O	CO2	Н2
n	0,218	0,438	0,672	0,562
N	0,115	0,232	0,355	0,297
ån=1,89

ξ₁₂=-0,11

R₂₂ выходR₂₂ входR₁₃

2CO CO2+C (тв)

	CO	H2O	CO2	Н2
n	0,106	0,438	0,728	0,562
N	0,057	0,239	0,397	0,306
ån=1,834

ξ₂₂=0,056

выходR₁₃ входR₂₃

R₁₃

2CO CO2+C (тв)

	CO	H2O	CO2	Н2
n	0,163	0,495	0,671	0,505
N	0,089	0,270	0,366	0,275
ån=1,834

ξ₁₃=-0,057

выходR₂₃ входR₁₄

	CO	H2O	CO2	Н2
n	0,099	0,495	0,703	0,505
N	0,055	0,275	0,390	0,280
ån=1,802

R₂₃

CO+H2O CO2+C (тв)

ξ₂₃=0,032

R₁₄ выходR₁₄ входR₂₄

CO+H2O CO2+H2

	CO	H2O	CO2	Н2
n	0,139	0,535	0,663	0,465
N	0,077	0,297	0,368	0,258
ån=1,802

ξ₁₄=-0,04

выходR₂₄ входR₁₅

2CO CO2+C(тв)

	CO	H2O	CO2	Н2
n	0,101	0,535	0,682	0,465
N	0,056	0,300	0,382	0,261
ån=1,783

R₂₄

ξ₂₄=0,0195

выходR₁₅ входR₂₅

R₁₅

CO +H2O CO2+H2

	CO	H2O	CO2	Н2
n	0,121	0,555	0,662	0,445
N	0,068	0,311	0,371	0,250
ån=1,783

ξ₁₅=-0,02

входR₂₅ выходR₁₆

	CO	H2O	CO2	Н2
n	0,099	0,555	0,672	0,445
N	0,056	0,313	0,379	0,251
ån=1,772

R₂₅

2CO CO2+C (тв)

ξ₂₅=0,011

	CO	H2O	CO2	Н2
n	0,114	0,570	0,659	0,432
N	0,064	0,321	0,371	0,243
ån=1,775

выходR₁₆ входR₂₆

R₁₆

CO+H2O CO2+H2

ξ₁₆=-0,015

выходR₂₆ входR₁₇

	CO	H2O	CO2	Н2
n	0,098	0,570	0,667	0,432
N	0,055	0,332	0,377	0,244
ån=1,767

R₂₆

2CO CO2+C (тв)

ξ₂₆=0,0075

R₁₇

CO+H2O CO2+H2

выходR₁₇ входR₂₇

	CO	H2O	CO2	Н2
n	0,110	0,582	0,655	0,420
N	0,062	0,329	0,370	0,237
ån=1,767

ξ₁₇=-0,012

2CO CO2+C (тв)

R₂₇ выходR₂₇ входR₁₈

	CO	H2O	CO2	Н2
n	0,099	0,582	0,661	0,420
N	0,056	0,330	0,375	0,238
ån=1,761

ξ₂₇=0,0057

	CO	H2O	CO2	Н2
n	0,107	0,590	0,653	0,412
N	0,061	0,335	0,371	0,234
ån=1,762

R₁₈

CO+H2O CO2+H2

выходR₁₈ входR₂₈

ξ₁₈=-0,008

выходR₂₈ входR₁₉

	CO	H2O	CO2	Н2
n	0,098	0,590	0,657	0,412
N	0,056	0,336	0,374	0,234
ån=1,757

R₂₈

2CO CO2+C (тв)

ξ₂₈=0,0045

CO+H2O CO2+H2

выходR₂₈ входR₁₉

	CO	H2O	CO2	Н2
n	0,104	0,596	0,651	0,406
N	0,059	0,339	0,370	0,231
ån=1,757

R₂₉

ξ₂₉=-0,006

выход R₂₉

	CO	H2O	CO2	Н2
n	0,098	0,596	0,654	0,406
N	0,056	0,340	0,373	0,231
ån=1,754

R₂₉

2CO CO2+C (тв)

ξ₂₉=0,003

Задача 3.3.17

Определите состав равновесной смеси при протекании в газовой фазе процесса при T=600K и общем давлении P=1атм

(1)

(2)

Исходный состав соответствует стехиометрии . Продукты реакции в исходной смеси отсутствуют.

Решение.

Поскольку обе реакции идут без изменения числа молей, то .

Поскольку общее давление в системе P=1атм, то систему можно рассматривать как идеальную, а значит K_γ=1 и K_a(Т) = K_р(Т).

Тогда можно записать:

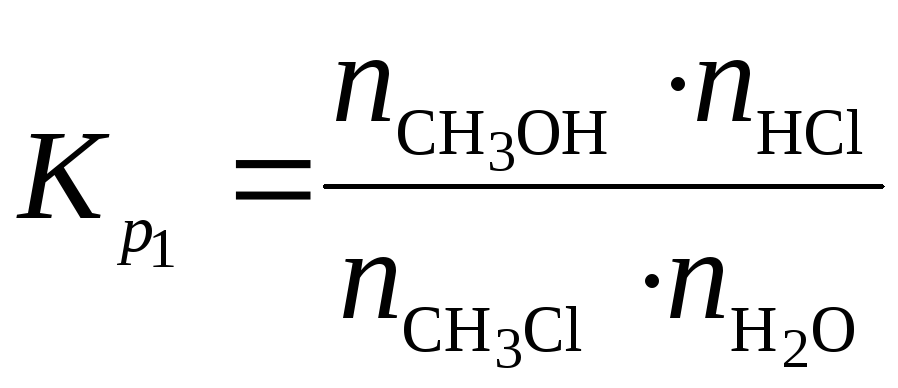(а)

и

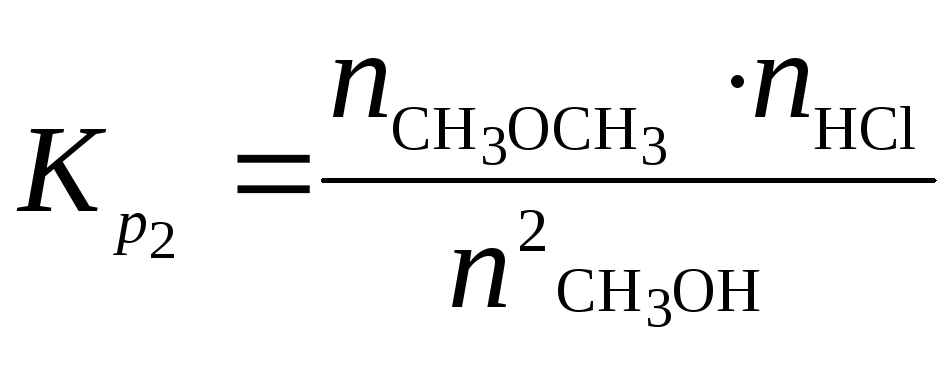(б)

При решении такого типа задач возможны два подхода.

Подход первый, основанный на совместном решении системы уравнений (а) и (б).

Введем обозначения: x-количество HCl, моль в равновесной смеси(в соответствии со стехиометрией реакции, такое же количество CH₃Cl и H₂O прореагировало и CH₃OH образовалось по первой реакции); y- количество CH₃OCH₃,моль,в равновесной смеси (в соответствии со стехиометрией такое же количество H₂O образовалось и в два раза большее количество CH₃OH прореагировало по второй реакции).

Тогда при равновесии(активности или концентрации реагентов в момент равновесия должны удовлетворять всем уравнениям, связывающим K_p c составом для любой реакции!) количество каждого вещества, моль: С учетом этих обозначений (а) (б) можно записать :

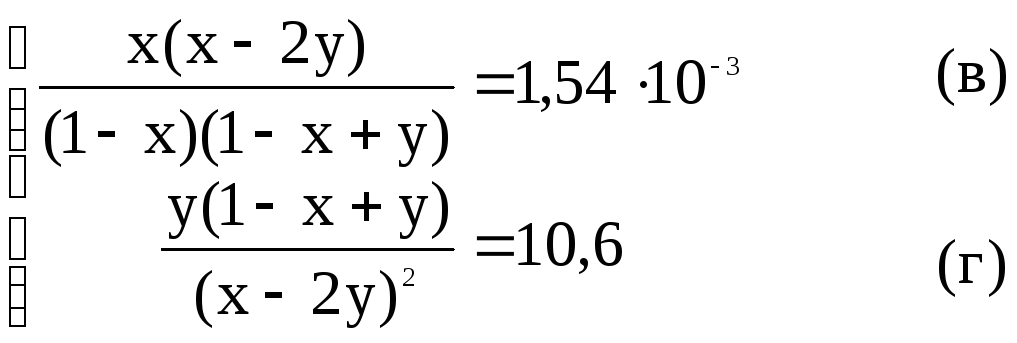
Задача сводится к решению системы двух нелинейных уравнений с двумя неизвестными.

Такая система может быть решена, например, с помощью программы, реализующей, итерационный метод с модификацией Зейделя.Напомним, что для сходимости метода решения необходимо условие: суммы модулей частных производных каждой функции по всем переменным не должны превышать единицу.

Выполняя это требование, преобразуем (в) и (г). Соответственно получим:

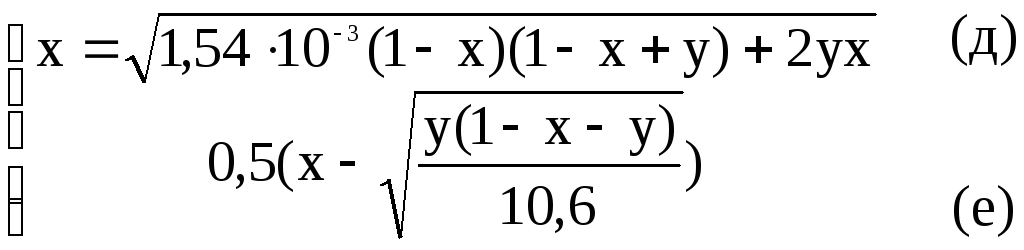
Программная реализация метода может быть осуществлена или с помощью ПЭВМ или с помощью ПМК [7]. В [7] приведены соответствующие программы расчета и его результаты: .

Таким образом, состав равновесной смеси, моль:

CH3Cl	H2O	CH3OH	CH3OCH3	HCl
0,9518	0,9613	0,029	0,0094	0,0481

Подход второй, основанный на методе последовательно соединенных реакторов (см. отступление третье.)

Этот метод позволяет вместо системы нелинейных уравнений (в рассматриваемом случае системы двух уравнений (а) и (б)) решать последовательно нелинейные уравнения (а) и (б) с одной неизвестной. В этом случае процесс последовательных решений производят до тех пор, пока степень превращения( или химическая переменная) не станет меньше некоторой наперед заданной величины, а равновесный состав практически не изменяется, разумеется, в заданных пределах.

Рассмотрим еще раз практическое применение этого метода( см. также задачу 3.3.16).

Для реакции (1) (учитывая стехиометричность начального состава) выразим равновесный состав через начальный и химическую переменную ξ_1j, где 1- номер реактора R₁, в котором протекает реакция (1), j-номер “прохода” через этот реактор. Тогда после первого “прохода”:

(1)

равновесный 1-ξ₁₁ 1-ξ₁₁ ξ₁₁ ξ₁₁

состав, моль

Значение ξ₁₁, а следовательно, и равновесный состав на выходе из реактора R₁₁ после первого “прохода” находят из соотношения (а), связывающего равновесный состав и константу равновесия:

Реакционная смесь такого состава поступает во второй реактор R_2j, где протекает реакция (2). В реакторе R₂ устанавливается равновесие реакции (2).

(2)

исходный

состав, моль ξ₁₁ 0 ξ₁₁

равновесный

состав, моль n₁₁-2ξ₂₁ ξ₂₁ n₁₁+ξ₂₁

Теперь находят h₂₁, используя связь между и равновесным составом во второй реакции.

Находят равновесный состав на выходе из второго реактора R₂₁ после первого «прохода»:

Этот состав снова поступает в первый реактор R₁₂, где осуществляется второй проход:

(1)

исходный

состав, моль

Из соотношения:

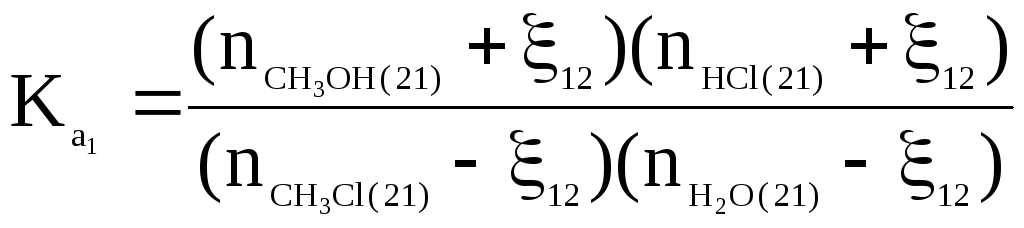
определяют ξ₁₂ и равновесный состав на выходе из первого реактора после второго прохода который поступает во второй реакторR₂₂ ,

где осуществляется второй “проход”, и.т.д.

Указанную процедуру проводят, пока не будут выполнены наперед заданные условия относительно значений ξ_ij.

Последовательность расчетов и его результаты иллюстрируются схемой, в которой R_ij и ξ_ij соответственно i-ый реактор и значение химической переменной в i-ом реакторе после j-го “прохода”.

CH₃Cl H₂O CH₃OH HCl

1 1 0 0 выход R₁₁ вход R₁₂

CH3Cl	H2O	CH3OH	HCl
0,9623	0,9623	0,0377	0,0377

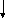выход вход R₁₁

вход R₁₁

R11

R21

ξ₁₁=0,0377 å=2

CH3Cl	H2O	CH3OH	CH3OCH3	HCl
0,9623	0,9688	0,0247	0,0065	0,0377

ξ₁₂=0,0065

CH3Cl	H2O	CH3OH	CH3OCH3	HCl
0,9498	0,9613	0,0322	0,0065	0,0452

R12

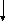
ξ₂₁=0,0075

R22

CH3Cl	H2O	CH3OH	CH3OCH3	HCl
0,9498	0,9633	0,0282	0,0085	0,0452

x₂₂=0,002

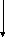
R13

CH3Cl	H2O	CH3OH	CH3OCH3	HCl
0,9478	0,9613	0,0302	0,0085	0,0472

x₃₁=0,002

R23

CH3Cl	H2O	CH3OH	CH3OCH3	HCl
0,9478	0,9620	0,0288	0,0092	0,0472

x₂₃=0,0007

R14

CH3Cl	H2O	CH3OH	CH3OCH3	HCl
0,9472	0,9614	0,0294	0,0092	0,0478

x₄₁=0,0006

R24

CH3Cl	H2O	CH3OH	CH3OCH3	HCl
0,9472	0,96155	0,0291	0,00935	0,0478

x₂₄=0,00015