
- •Расчётные задачи химической термодинамики
- •Глава 1.
- •Если использовать средние значения теплоемкости и плотностив заданном температурном интервале, то объемная плотность аккумулированной энергии равна:
- •Задача 1.3.4
- •Задача 1.3.6
- •Задача 1.38
- •1.4 Задачи
- •Глава 2. Тепловые эффекты физико-химических процессов.
- •2.1. Цели изучения
- •2.2. Основные закономерности.
- •Для реакций с участием идеальных газов
- •2.3. Основные задачи
- •Отметим, что рассматриваемая реакция протекает наряду с реакциями
- •Задача 2.3.4.
- •Глава 3.
- •В некоторых случаях можно воспользоваться значениями средних
- •3.3. Основные задачи.
- •Задача 3.3.2
- •Задача 3.3 Определите возможность протекания процесса
- •Решение
- •Задача. 3.3.4
- •Задача 3.3.5
- •Решение
- •Решение
- •Решение уравнения с помощью эвм - секунды, но почти с той же
- •Задача 3.3.8
- •Согласно [1], логарифм константы равновесия реакции образования
- •Исходя из этих соображений, проследим влияние давления на вели-
- •Выразим связь между константой равновесия и равновесным соста-
- •Задача 3.3.13
- •3.4. Многовариантные задачи.
Согласно [1], логарифм константы равновесия реакции образования
N H3
из простых веществ, т.е. по реакции
1/2N2+3/2H2
NH3
H3
из простых веществ, т.е. по реакции
1/2N2+3/2H2
NH3
при
800К
![]() .
Следовательно, для реакции
.
Следовательно, для реакции
3 H2+N2
2NH3
H2+N2
2NH3
![]() .
.
Тогда в соответствии с (3.39):
![]()
откуда
![]()
и
![]()
Следовательно, если парциальное давление NH3 в смеси меньше давления H2 и N2, то может происходить синтез аммиака.
Задача 3.3.10
При изучении реакции синтеза аммиака Ф. Габер получил при 673К
следующие результаты по равновесному составу при различном общем
давлении
в системе (![]() -мольная
доля аммиака в равновесной смеси):
-мольная
доля аммиака в равновесной смеси):
|
|
| |||||||
|
1 |
10 |
30 |
50 |
100 |
300 |
600 |
1000 | |
|
0.0021 |
0.0204 |
0.058 |
0.0917 |
0.1636 |
0.355 |
0.536 |
0.694 | |
Определите, при каких давлениях систему можно считать идеальной и при каких давлениях при расчете равновесий необходимо учитывать
неидеальность системы.
Решение.
Термодинамическая
константа равновесия
![]() ,
определяемая согласно (3.33) как
,
определяемая согласно (3.33) как![]()
не зависит ни от давления, ни от концентрации, а определяется только природой реагирующих веществ и температурой.
Для
идеальных систем
![]()
Однако
при достаточно высоких давлениях
значение
![]() ;
;
рассчитанное
по экспериментальным данным о
![]() изменяется с изменением давления, что
может служить критерием непременимости
изменяется с изменением давления, что
может служить критерием непременимости
для таких давлений законов идеальных систем.
Исходя из этих соображений, проследим влияние давления на вели-
ч ину
ину![]() исследуемой реакции: 1/2N2+3/2H2
NH3
исследуемой реакции: 1/2N2+3/2H2
NH3
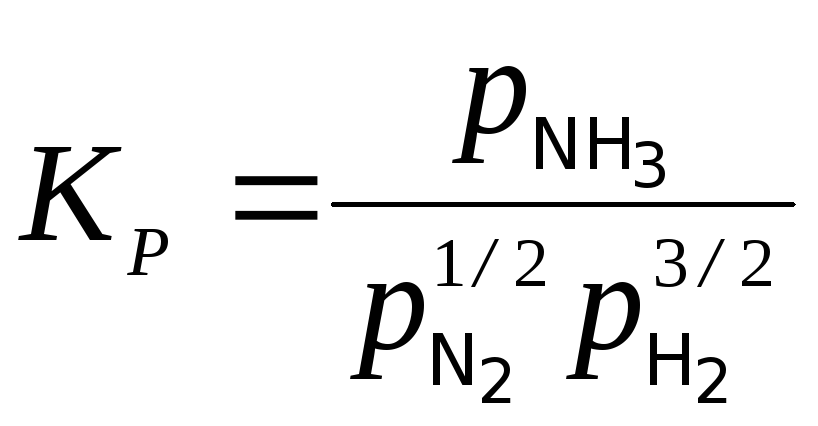
Выразим
![]() через мольные доли компонентов при
равновесии и общее давление в системе.
Поскольку парциальное давление
через мольные доли компонентов при
равновесии и общее давление в системе.
Поскольку парциальное давление![]()
компонента
![]() и его мольная доля
и его мольная доля![]() связаны соотношениями
связаны соотношениями
![]() ,
где
,
где
![]() -
общее давление в системе, можно записать:
-
общее давление в системе, можно записать:
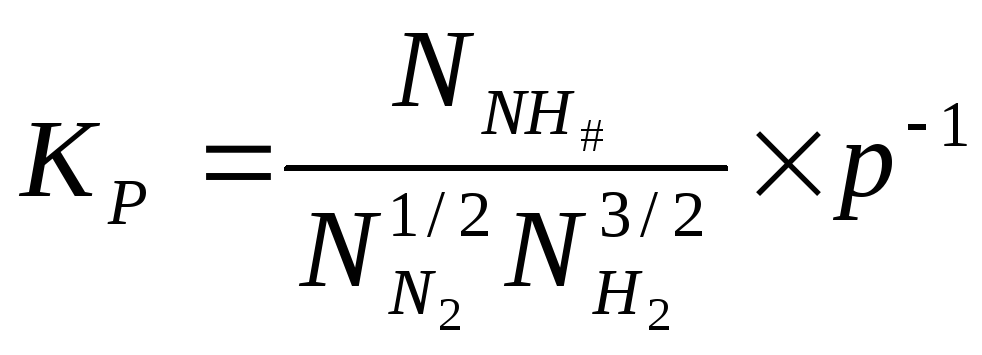
Если
мольная доля аммиака
![]() ,
то, т.к. соотношение
,
то, т.к. соотношение![]() и
и![]()
Тогда
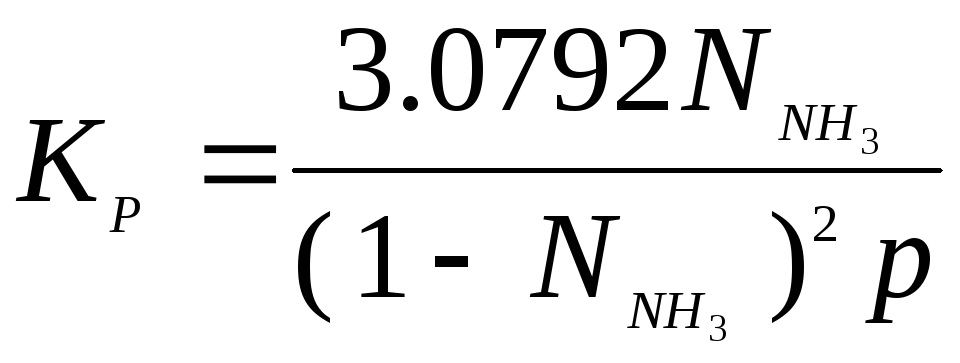
Полученное соотношение позволяет рассчитать по имеющимся экспе-
риментальным
данным значение
![]() при
различных давлениях.
при
различных давлениях.
|
|
1 |
10 |
30 |
50 |
100 |
300 |
600 |
1000 |
|
|
0.0021 |
0.0204 |
0.058 |
0.0917 |
0.1636 |
0.355 |
0.536 |
0.694 |
|
|
0.00649 |
0.00654 |
0.0067 |
0.00684 |
0.00720 |
0.00876 |
0.0128 |
0.02282 |
Анализ
значений
![]() при
различных давлениях позволяет сделать
вывод, что при давлении выше 50 атм система
не может рассматриваться как идеальная
и для расчета равновесия при этих
температурах необходимо учитывать
летучести этих компонентов.
при
различных давлениях позволяет сделать
вывод, что при давлении выше 50 атм система
не может рассматриваться как идеальная
и для расчета равновесия при этих
температурах необходимо учитывать
летучести этих компонентов.
Задача 3.3.11
Проследите влияние температуры на равновесный состав в реакции
с интеза
аммиака 3H2+N2
2NH3
при стехиометрическом соотношении
исходных веществ и общем давлении p=
20 атм
интеза
аммиака 3H2+N2
2NH3
при стехиометрическом соотношении
исходных веществ и общем давлении p=
20 атм
Решение.
Рассчитаем
равновесный состав при двух температурах
![]() и
и
![]() ,
считая (см. предыдущую задачу), что при
p
= 20 атм сис-
,
считая (см. предыдущую задачу), что при
p
= 20 атм сис-
тему
можно рассматривать как идеальную и
![]() .
.
Выразим связь между константой равновесия и равновесным соста-
вом
(при этом будем использовать химическую
переменную
![]()
 3H2
+ N2
2NH3
3H2
+ N2
2NH3
Исходный
![]()
![]()
![]()
состав, моль
Состав
при
![]()
![]()
![]()
равновесии
Сумма числа молей в равновесной смеси
![]()
С
учетом этого и учтя, что
![]() можно записать (3.46):
можно записать (3.46):
![]()
После упрощения и подстановки значения P = 20атм:
![]()
Значения
![]() исследуемой реакции найдем через
константы равновесия
исследуемой реакции найдем через
константы равновесия
реакций
образования аммиака
![]() при
температурах 500К и 800К [1]:
при
температурах 500К и 800К [1]:![]()
|
|
|
|
|
|
500 |
-0.48 |
-0.96 |
0.11 |
|
800 |
-2.46 |
-4.92 |
1.2 |
Тогда для 500К можно записать:
![]()
или
![]() (а)
(а)
и для 800К
![]() (б)
(б)
Поиск решения этих уравнений с использованием ПЭВМ занимает секунды. Однако не стоит отчаиваться, если под рукой только калькулятор: решение займет несколько минут, если воспользоваться способом, описанным во втором отступлении.
Запишем уравнение (а) в виде:
![]()
Решение
![]() будем искать с точностью до 0.01. Учтя,
что область
будем искать с точностью до 0.01. Учтя,
что область
определения
![]()
![]() ,
зададим
,
зададим
![]() :
:
![]()
![]()
![]()
![]()
Следовательно,
решение
![]() .
Тогда, разделив отрезок пополам:
.
Тогда, разделив отрезок пополам:
![]()
![]()
Продолжим
процедуру
![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
И, наконец, последняя итерация:
![]()
![]()
Таким
образом, при температуре 500К и давлении
20атм. равновесный состав будет
характеризоваться следующим соотношением
между компонентами (учтя связь между
числом молей
![]() и химической переменной (3.45), мольной
долей
и химической переменной (3.45), мольной
долей
![]() и
химической переменной (3.48), а также
степенью превращения
и
химической переменной (3.48), а также
степенью превращения ![]() и химической переменной (3.47)):
и химической переменной (3.47)):
|
|
|
|
|
|
|
|
|
|
1.35 |
0.975 |
0.325 |
0.51 |
0.37 |
0.12 |
0.675 |
0.675 |
Для
решения уравнения (б) понадобится меньше
итераций, если при выборе первого
значения
![]() руководствоваться следующими
соображениями: если
руководствоваться следующими
соображениями: если
![]() очень
мало, то
очень
мало, то
![]() должно
быть близко к нулю. Тогда, подставив в
выражение, стоящие в скобках уравнения
(б)
должно
быть близко к нулю. Тогда, подставив в
выражение, стоящие в скобках уравнения
(б)![]() ,
получим в первом приближении:
,
получим в первом приближении:![]() ,
откуда
,
откуда![]()
Подставляя
теперь вместо
![]() полученное значение
полученное значение![]() :
:
![]()
И,
наконец, подставив
![]() :
:
![]()
Тогда равновесный состав при 800К и давлении р=20атм:
|
|
|
|
|
|
|
|
|
|
0.084 |
2.874 |
0.958 |
0.02 |
0.73 |
0.24 |
0.042 |
0.042 |
Таким образом, при повышении температуры содержание аммиака в равновесной смеси уменьшается, поскольку Синтез аммиака - процесс обрати-
мый, протекает с уменьшением объема и выделением тепла. В соответствии с принципом Ле-Шателье (3.2.42) равновесие смещается в сторону образования аммиака при повышении давления и понижении темпера-
туры.
Тем
не менее, в производственных условиях
процесс ведут на катализаторе при ![]() ,
поскольку при более низких (и выгодных
для равновесного выхода) температурах
скорость синтеза весьма мала, а
катализаторов, обеспечивающих при
низких температурах приемлемую скорость
пока (пока?) не существует.
,
поскольку при более низких (и выгодных
для равновесного выхода) температурах
скорость синтеза весьма мала, а
катализаторов, обеспечивающих при
низких температурах приемлемую скорость
пока (пока?) не существует.
Задача 3.3.12.
Исследуйте влияние температуры на термодинамическую константу рав-
новесия
![]() реакции.
реакции.
C O+H2O(газ)
CO2+H2
O+H2O(газ)
CO2+H2
Какие выводы могут быть сделаны по полученным данным об условиях про-
ведения этого процесса, используемого в промышленности для получения водорода.
Решение.
К онстанта
равновесия
онстанта
равновесия![]() может быть рассчитана различными
способами - иногда выбор способа
определяется наличием тех или иных
необходимых справочных данных.
может быть рассчитана различными
способами - иногда выбор способа
определяется наличием тех или иных
необходимых справочных данных.
Попробуем
определить
![]() данной реакции различными способами,
оценим их "трудоемкость" и сравним
полученные результаты.
данной реакции различными способами,
оценим их "трудоемкость" и сравним
полученные результаты.
1.
Расчет на основании данных о логарифмах
констант равновесия
![]()
веществ, участвующих в реакции (3.35).
Расчет удобно провести в матричной форме (см. отступление 1) как произ-
ведение
матрицы характеристик (матрицы логарифмов
констант равновесия реакций образования
![]() )
и вектора-столбца стехиометрических
коэффициентов (стехиометрические
коэффициенты исходных веществ со знаком
"-"). Напомним, что в системеMathCAD
пред-
)
и вектора-столбца стехиометрических
коэффициентов (стехиометрические
коэффициенты исходных веществ со знаком
"-"). Напомним, что в системеMathCAD
пред-
усмотрены специальные матричные операторы.
 CO
+ H2O(газ)
CO2
+ H2
CO
+ H2O(газ)
CO2
+ H2

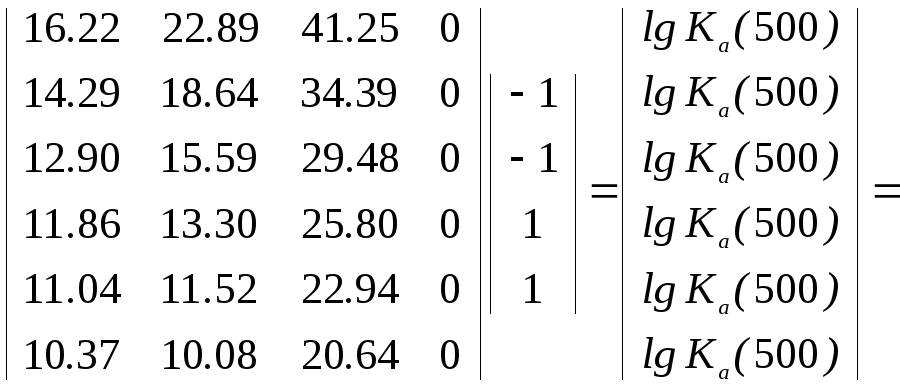

|
T,K |
500 |
600 |
700 |
800 |
900 |
1000 |
|
|
138.0 |
28.84 |
9.77 |
4.36 |
2.40 |
1.55 |
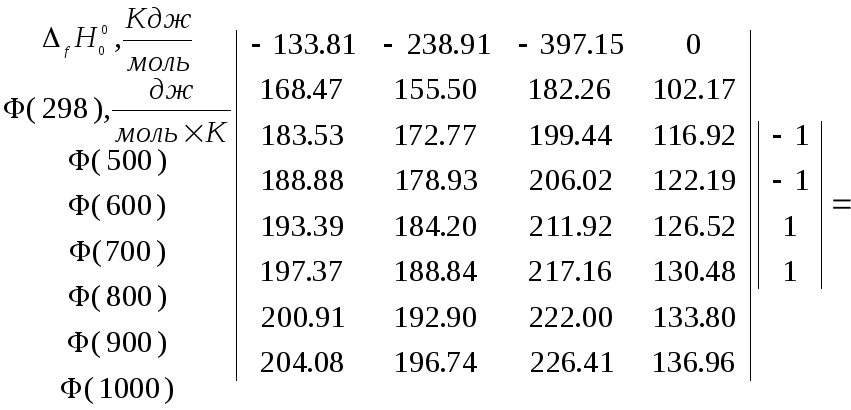
2.Расчет
по данным о приведенных энергиях Гиббса
![]()
(3.34)
 CO
+ H2O(газ)
CO2
+ H2
CO
+ H2O(газ)
CO2
+ H2
=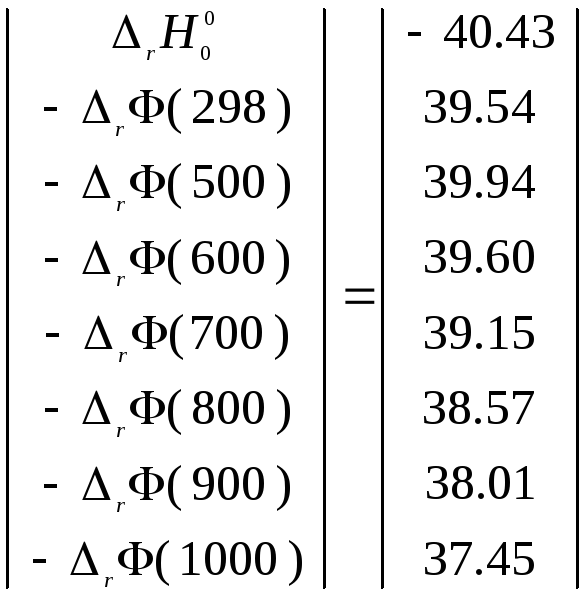
Тогда в соответствии с (3.34)
![]()
и
после подстановки значений
![]() и
и![]()
![]() получим:
получим:
|
T, K |
298 |
500 |
600 |
700 |
800 |
900 |
1000 |
|
|
11.56 |
4.92 |
3.34 |
2.24 |
1.44 |
0.83 |
0.36 |
|
|
10482.0 |
137.0 |
28.22 |
9.39 |
4.22 |
2.29 |
1.43 |
3.
Расчет по данным о зависимости
![]()
Проведем
вначале расчет в приближении независимости
![]() и
и![]() от температуры, т.е. считая
от температуры, т.е. считая![]() и
и
![]() .
.
Тогда
![]()
и
![]()
Рассчитаем
согласно Гессу значения
![]() и
и![]()
 CO
+ H2O(газ)
CO2
+
H2
CO
+ H2O(газ)
CO2
+
H2

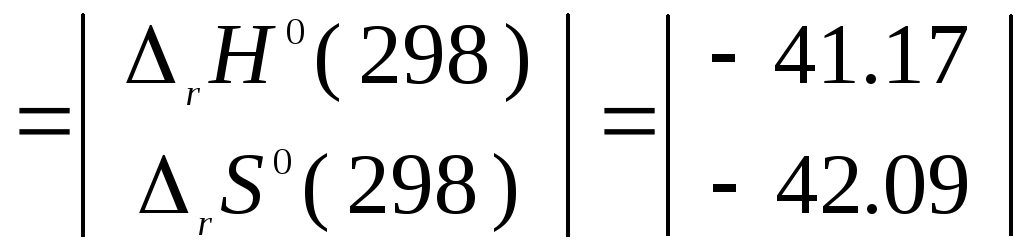
Тогда
![]()
Полученное
соотношение позволяет рассчитать
![]() при
различных температурах:
при
различных температурах:
|
T,К |
298 |
500 |
600 |
700 |
800 |
900 |
100 |
|
|
11.56 |
4.84 |
3.20 |
2.02 |
1.13 |
0.44 |
-0.11 |
|
|
10482.0 |
126.4 |
24.5 |
7.5 |
3.1 |
1.5 |
0.89 |
Теперь
проведем расчет, учитывающий влияние
температуры на
![]() и
и![]() ,
т.е. по соотношению
,
т.е. по соотношению
![]() ,
,
где
![]() .
.
Учитывая
зависимости
![]() и
и![]() от
температуры (), можно записать:
от
температуры (), можно записать:
![]()
Последнее уравнение представим в виде:
![]()
![]() ,
,
где
![]() и
и![]() - коэффициенты, зависящие только от
температуры, значения которых приведены
в справочных пособиях [1] с шагом в 100К.
В отечественной литературе этот прием
называют методом
- коэффициенты, зависящие только от
температуры, значения которых приведены
в справочных пособиях [1] с шагом в 100К.
В отечественной литературе этот прием
называют методом
Темкина-Шварцмана.
Введем обозначение:
![]() .
.
Тогда предыдущее выражение можно записать:
![]() (а)
(а)
которое отличается от приближенного значения
![]() (б)
(б)
слагаемым
![]() .
.
Но
![]() (в)
(в)
и
![]() ,
(г)
,
(г)
где
![]() - значение константы активности,
рассчитанное в приближении к
- значение константы активности,
рассчитанное в приближении к
независимости
![]() и
и![]() от
температуры.
от
температуры.
Сравнивая (а) - (г) можно получить
![]()
или (9)
![]()
Последнее выражение даёт возможность оценить погрешность, которая может быть совершена при использование приближений (б) и (г) при расчете константы равновесия.
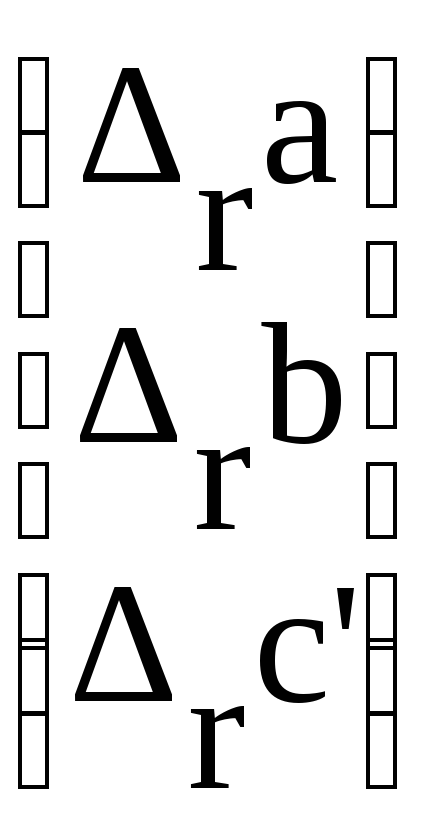
Рассчитаем теперь константу равновесия Кa (т) исследуемого процесса.
В начале найдём значения r ,r и r С.
CO + H2O(газ) CO2 + H2

![]()
a
b =
c'
 =
=
 =
=
Следовательно
А=13,01Mо -2,51 10-3 М1-7,91 105М-2
Найдём значение Мo ,М1 и М2 в зависимости от температуры 1:
|
Т,К |
500 |
600 |
700 |
800 |
900 |
1000 |
|
Мo |
0,1133 |
0,1962 |
0,2794 |
0,3957 |
0.4361 |
0,5088 |
|
10-3М1 |
0,0407 |
0,0759 |
0,1153 |
0,1574 |
0,2012 |
0,2463 |
|
105 М2 |
0,0916 |
0,1423 |
0,1853 |
0,2213 |
0,2521 |
0.2783 |
( Попробуем в начале оценить – необходим ли точный расчет Кa (т) в
Этой области температур или можно ограничиться приближенным
расчетом и тем самым несколько облегчить трудную студенческую жизнь.
Для
этого рассчитаем согласно (д) значения
![]() на
концах
на
концах
температурного интервала:
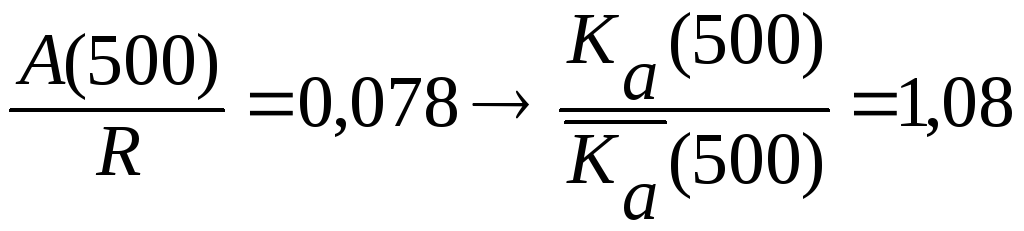
![]() Следовательно,
приближенное и точное значение Кa(500)
практически
Следовательно,
приближенное и точное значение Кa(500)
практически
Совпадает, но при 1000 К различаются в 1,5 раза.
Если такая точность нас удовлетворяет, то можно ограничиться
приближенным расчетом. По крайней мере мы будем знать, какую
Ошибку допускаем при этом).
Теперь, используя соотношения (a) и (в) , рассчитаем значения Кa(T) :
|
T, k |
500 |
600 |
700 |
800 |
900 |
1000 |
|
A(T) |
0,6474 |
1,2371 |
1,8800 |
2,5207 |
3,1746 |
3,800 |
|
|
0,078 |
0,1488 |
0,2262 |
0,303 |
0,382 |
0,4573 |
|
ln Ka (T) |
4,93 |
3,35 |
2,24 |
1,43 |
0,83 |
0,35 |
|
Кa (T) |
138,4 |
28,50 |
9,39 |
4,18 |
2,29 |
1,42 |
Сравнивая значения Кa (т), полученные различными методами, отметим, что наиболее точные результаты получены при расчете с использованием приведенной энергии Гиббса Ф(т) (3,34)
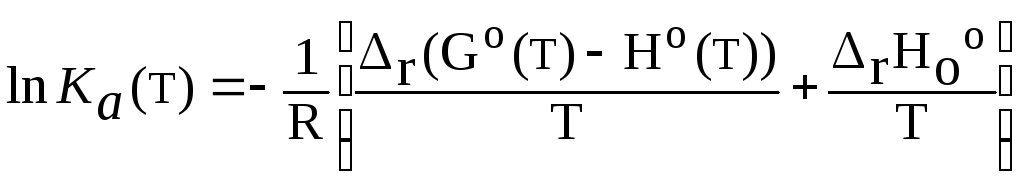 (3,34)
(3,34)
Поскольку значения Ф(т) получены по микроскопическим
данным, а также по данным о зависимости
![]() (3,34)
(3,34)
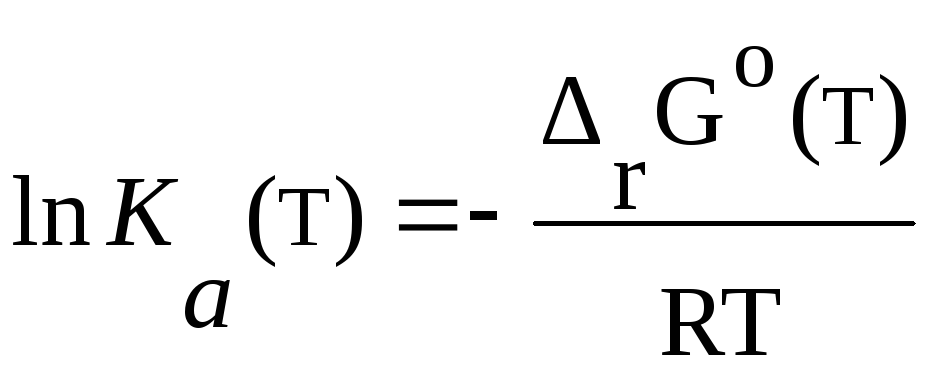 (3,38)
Значения Кa(т),полученные
по данным о константах равновесия
реакции образования участников реакции
Kf(т)
(3,35),менее точны, поскольку значение ln
Kf
(т)[1]
получены с использованием средних
значений теплоемкости. Наименее
точные результаты, что и следовало
ожидать, получены без учета влияния
температуры на rHo
и rSo:
(3,38)
Значения Кa(т),полученные
по данным о константах равновесия
реакции образования участников реакции
Kf(т)
(3,35),менее точны, поскольку значение ln
Kf
(т)[1]
получены с использованием средних
значений теплоемкости. Наименее
точные результаты, что и следовало
ожидать, получены без учета влияния
температуры на rHo
и rSo:
rC(т)=rHo(газ)-ТrSo(газ) (а)
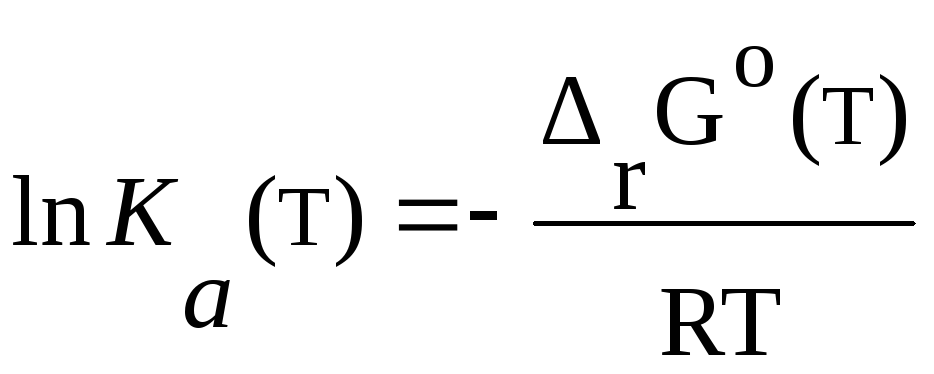 (б)
(б)
Сравнение результатов, полученных по соотношениям (3,38)
И (а;б)
|
Т,К |
500 |
600 |
700 |
800 |
900 |
1000 |
|
Кa (т) (3,38)
|
138,4 |
28,50 |
9,39 |
4,18 |
2,29 |
1,42 |
|
Кa(т) (а;б) |
126,4 |
24,5 |
7,5 |
3,1 |
1,5 |
0,89 |
Может, приведет к выводу, что различия между ними незначительны и практически не скажутся на равновесном составе. Этот вывод будет справедлив для рассматриваемой реакции, однако, обобщать его на все процессы было бы не корректно : сообщение между приближенным Ka(т) и точным Ka(т) значениями определяется соотношение (д):
![]()
Рассчитаем равновесный состав при Т=600К, используя точное значение Кa(600)=24,5 при Р.=1атм.
СО+ H2O(газ) СО2 +H2
Исходный
Состав, моль 1 1 0 0
Равновесный
состав 1- ξ 1-ξ ξ ξ
тогда
![]() и
и

и
![]() ;
;
![]()
Например, для реакции
CH4 = C(тв) + 2H2
|
ΔrHo (298) Кдж/моль |
ΔrSo(298) Дж/моль к |
Δa |
Δb 103 |
Δc |
Δc’ 10-5 |
|
74,88 |
80,51 |
57,12 |
-63,37 |
17,43 |
-7,54 |
Тогда приближенное значение Кa (т):
![]()
![]()
Точнее значение Ка (т) рассчитывали по соотношениям (а) и (д)
![]()
Расчет при температурах 1000. К и 1100R приводит
к значениям:
|
T, К |
1000 |
1100 |
|
|
0,67 |
1,49 |
|
|
1,95 |
4,43 |
|
А |
13,64 |
15,03 |
|
|
1,64 |
1,81 |
|
lnKa |
2,31 |
3,3 |
|
Кa |
10,07 |
27,11 |
Различие между приближенным Кa и точным Кa значениями в этом случае существенно, что, конечно, должно сказаться при расчете равновесного состава.
|
|
Реакция |
|
Состав,моль |
СH4C(тв)+2H2 |
|
исходный |
1 0 |
|
равновесный |
1- 2 |
|
Суммарное число молей при равновесный |
1+2 |
![]()
Где -химическая
переменная (3,43)
И тогда равновесный состав (в мольных долях)
![]() и
и
![]()
Теперь можно сравнить результаты расчета равновесного состава, полученные при использовании приближенного
Ka(т) и точного Ka(т) значений константы равновесия.
|
Т, К |
Равновесный состав | |||
|
Приближенный расчет |
Точный расчет | |||
|
|
|
|
| |
|
1000 |
0,33 |
0,67 |
0,43 |
0,57 |
|
1100 |
0,23 |
0,77 |
0,06 |
0,94 |
Расчет значений Ka (т) показал, что с увеличением температуры Ka (т) уменьшается, что следовалоожидать, поскольку исследуемая реакция –это экзотермическая(rHo (т)<0) и согласно принципу Ле Шателье при увеличении температуры равновесие смешается в сторону исходных веществ реакция протекает без изменения объема, поэтому
изменение давления (разумеется в тех приделах, когда Kj =1,т.е. систему можно рассматривать как идеальную).Не влияет на равновесный состав. Качественная и количественная оценка условий термодинамического равновесия позволяет сделатьвывод, что максимального выхода водорода можно достичь, проводя процесс при низких температурах.(нижний температурный предел процесса ограничен условиями конденсации водяного пара: при проведении
процесса под давлением 2-3 МПА этот предел составляет 180-200С)
Температурный режим определяется такими же свойствами
применяемых катализаторов: при использовании низкотяигнературных цинкхроммерных катализаторов реакции конвенции проводят при температуре 350-400С.
