Задача 3.3 Определите возможность протекания процесса

Al₂O_{3 (тв)} + 3SO_3(газ) → Al₂(SO₄)_3(тв)

В закрытой системе при стандартных условиях и температуре 298 К.

Решение

Критерием возможности протекания процесса в закрытой системе при постоянном давлении является (3.29) условие

По условию задачи обсуждается возможность проведения этого процесса при стандартных условиях, т.е парциальное давление SO₃ P(SO₃)=1.

Тогда должно выполнятся условие

Значение может быть рассчитано согласно закону Гесса по данным об энергиях Гиббса образованиякомпонентов реакции [1]:

Al₂O_{3 (тв)} + 3SO_3(газ) → Al₂(SO₄)_3(тв)

Следовательно, условие (3.29) соблюдается и в исследуемых условиях возможно протекание рассматриваемого процесса.

Задача. 3.3.4

В закрытой системе при стандартных условиях и 298 К для реакции

Al₂O_{3 (тв)} + 3SO_3(газ) → Al₂(SO₄)_3(тв)

. Возможен ли этот процесс при той же температуре в изолированной системе?

Решение.

Критерием возможности самопроизвольного протекания процесса в изолированной системе является условие (3.2)

,

то есть в изолированной системе самопроизвольно протекают процессы, идущие с ростом энтропии.

В исследуемом процессе (задача 3.3.1)

Следовательно, в изолированной системе процесс не возможен.

Задача 3.3.5

Определите температурный интервал, в котором в закрытой системе при стандартных условиях возможно самопроизвольное протекание процесса

Al₂O_{3 (тв)} + 3SO_3(газ) → Al₂(SO₄)_3(тв)

Решение

Критерием возможности самопроизвольного протекания процесса в закрытой системе при P,T = const является условие (3.29)

или (3.17)

где ирассчитываются согласно (2.10)

и (3.9)

а согласно (2.9)

Значения и коэффициенты∆a, ∆b и ∆с’ в (2.9) рассчитываются согласно закону Гесса.(Расчет для исследуемой реакции приведен в задаче 3.3.2)

Тогда после подстановки

и

в (3.17) получим, согласно (3.29), что самопроизвольный процесс возможен при температурах когда,

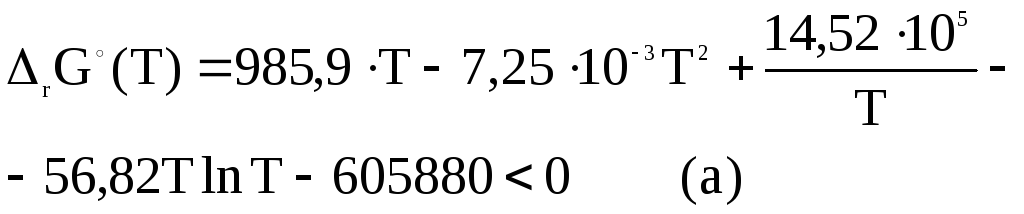
Таким образом задача свелась к решению неравенства.

Напомним, что полученная зависимость адекватно описывает изменения с температурой в области температур 298 – 1100 К, поскольку в этой области (см. задачу 3.3.2) адекватны зависимости Ср(Т) для всех компонентов реакции).

Если пренебречь изменением ис увеличением температуры, как отмечается в некоторых пособиях [5], то вместо неравенства (а) можно использовать

или для исследуемой реакции

Разумеется неравенство (б) решается мгновенно:

если 298  T<994,

но используя неравенство (б) мы не знаем, какую ошибку, или какую погрешность допускаем при определении температурного интервала.

Разумеется, решение неравенства (а) сопряжено с некоторыми вычислительными трудностями, которые удается избежать, если у Вас под рукой ПЭВМ. А если нет?

Отступление второе, в котором напоминается об одном достаточно простом методе решения нелинейных уравнений.

Гарантированную сходимость и простую программную реализацию решения уравнений F(x)=0 дает метод деления отрезка пополам [7].

Вернёмся к рассматриваемой задаче и проведём описанную процедуру для решения уравнения (а), помня ,что если имеется корень уравнения, т.е. некоторое значение для которой,то он должен находиться в температурном интервале 298–1100 К (весьма возможна ситуация, тогда при любом значении температуры) и рассчитаемна концах температурного интервала:

Вывод: значит _{на концах температурного интервала имеет разные знаки , следовательно, и при некоторой} ;

Можем уменьшить рассматриваемый интервал, учтя приближенное значение

и, если задана точность определения температурного интервала , то можно остановить расчёт: значениенаходится междуи, что отличается от приближенного значения 944К на 100К .

Задача 3.3.6.

Исследуйте возможность самопроизвольного процесса

при T=1050K