3.3. Основные задачи.
Задача 3.3.1. Какая из следующих реакций сопровождается наибольшим уменьшением и наибольшим увеличением энтропии при Т=const?
1.
2.
3.
4.
5.
6.
7.
8.
9.
Сделайте вначале качественный вывод, который затем подтвердите расчетом.
Решение.
Поскольку энтропия является мерой
неупорядоченности системы, то ее
качественное изменение (3.9) можно
определить по изменению числа молей
газообразных веществ
в результате реакции: если
,
то энтропия возрастает, причем, чем
больше
,
тем больше возрастание энтропии; если
<0,
то энтропия уменьшается.
Тогда для исследуемых реакций:
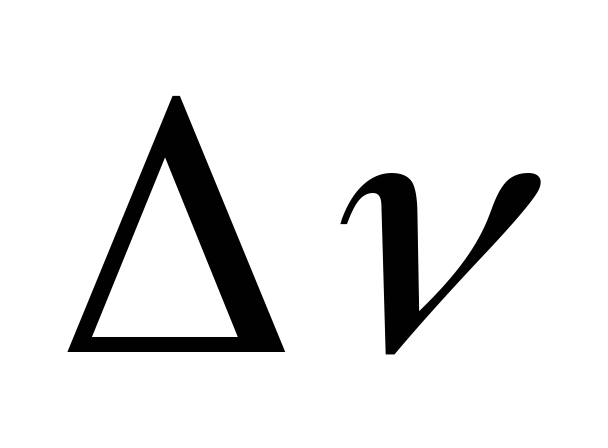=-1
Максимальное уменьшение числа молей
газообразных ве-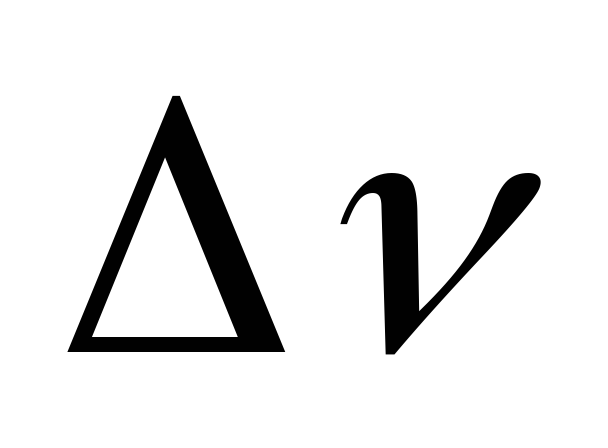
=
0 ществ
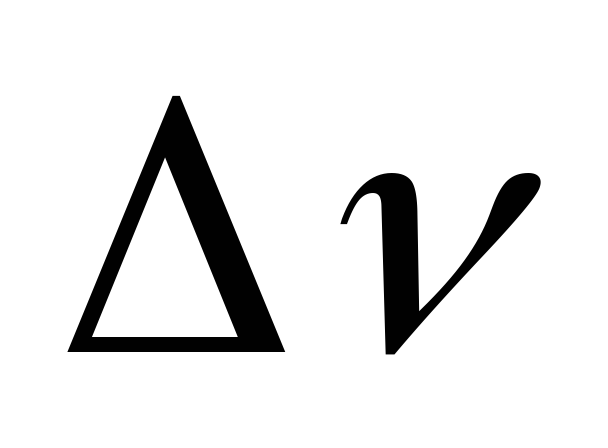происходит в результате реакции 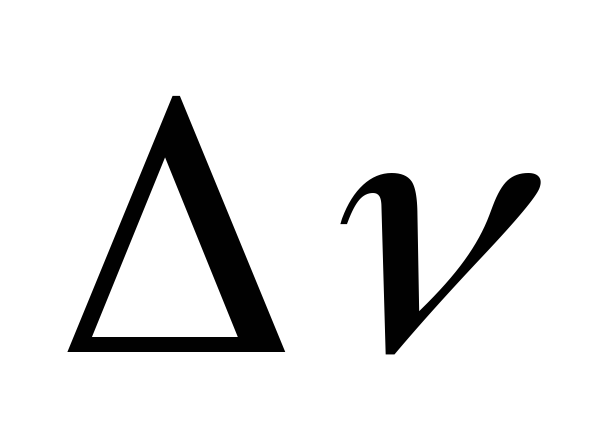(3):
=-3
.
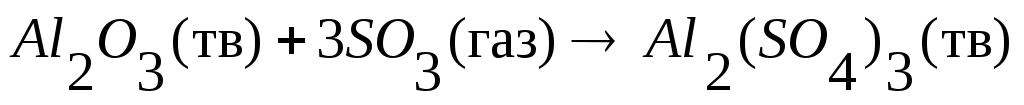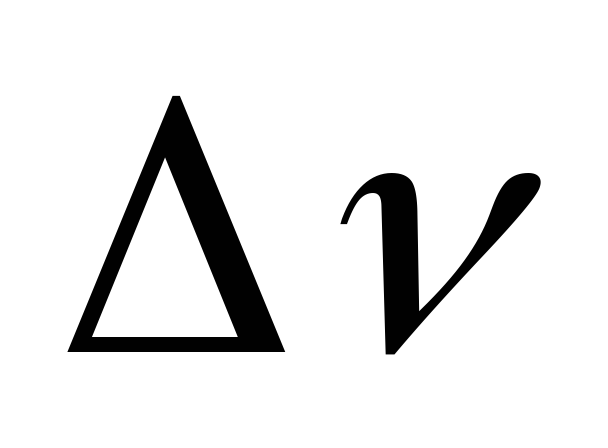=-2
Максимальное увеличение числа молей
газообразных ве-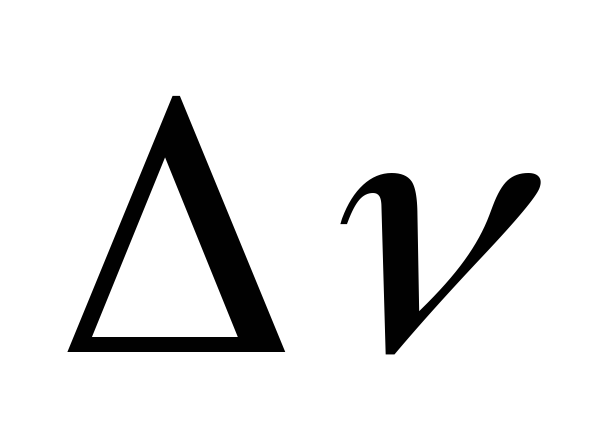 
=-2
ществ
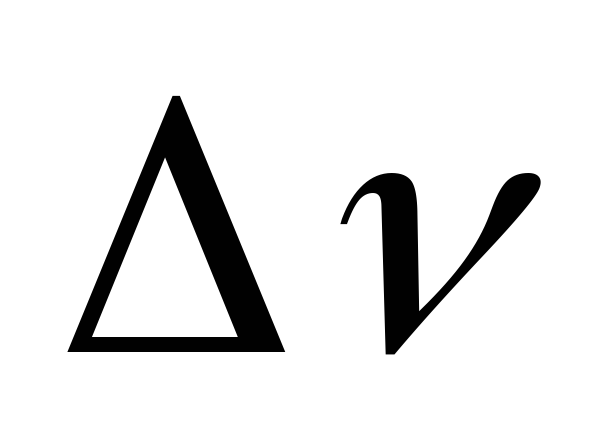происходит при протекании реакции (7):
=
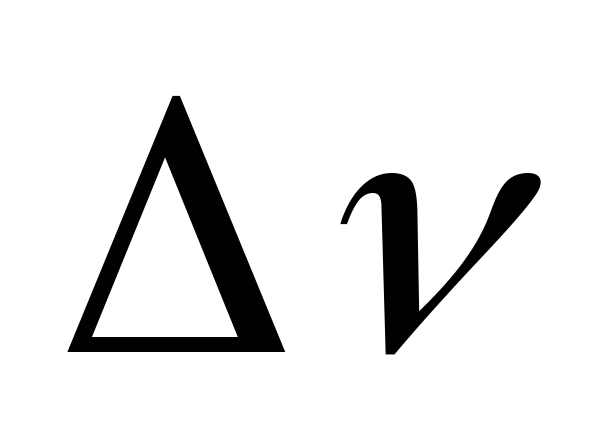1
.
=
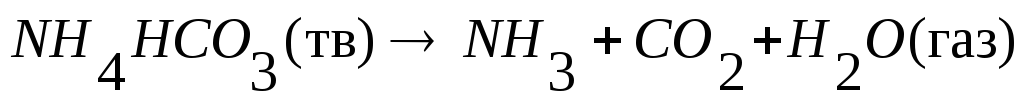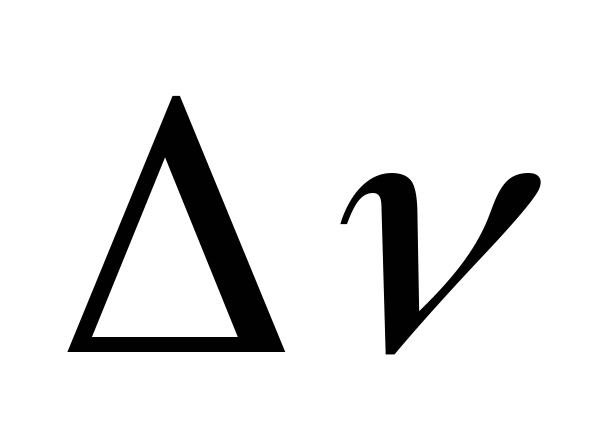3 Следовательно, в результате именно
этих реакций проис-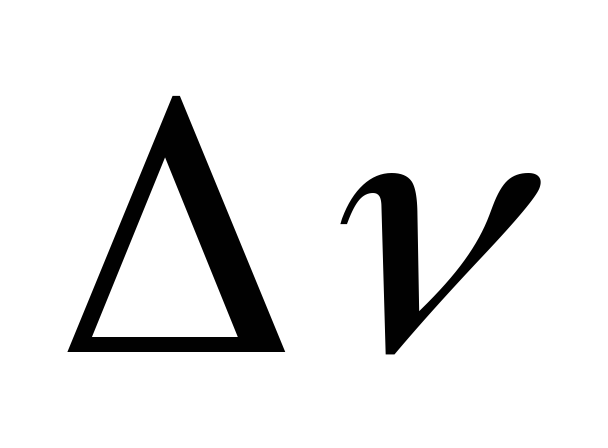
=
1 ходит максимальное уменьшение и
увеличение энтропии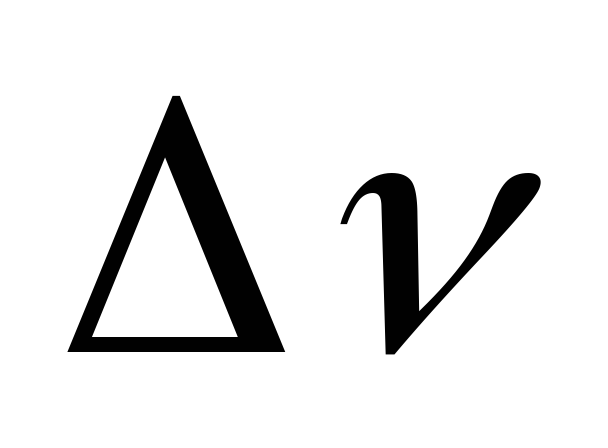 
=
1 системы.
Теперь
рассчитаем изменение энтропии
согласно закону Гесса, поскольку энтропия
является функцией состояния, т.е. ее
изменение определяется только конечным
и начальным состоянием системы и не
зависит от пути перехода из одного
состояния в другое.
Значение
энтропии найдем в
.
Расчет будем вести в матричной форме
(см. отступление 1.)
1.
,
(38.07 188.72 83.39)
=
-143.4
2.
,
(38.07 69.95 83.39)
=
-23.73
3.
,
(50.92 256.69 239.20)
=
-581.79
4.
,
(191.50 130.52 192.66)
=
-197.74
5.
,
(192.66 186.79 95.81)
=
-283.64
6.
,
(304.35 240.06)
=
175.77
7.
,
(120.8 192.66 213.66 188.72)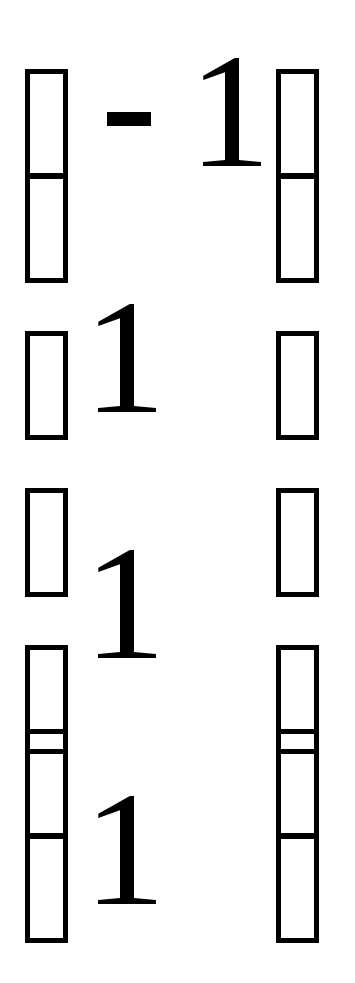 
=
474.24
8. CO2 + C(тв) → 2CO(газ)
9. CaCO3(тв)→CaO(тв) + CO2
Сравнение полученных данных подтверждает полученный вывод.
Задача 3.3.2
В реакциях:
1. Al2O3(тв)+3SO3(газ)→Al2(SO4)3(тв)
Энтропия при проведении процесса, при постоянной температуре T=298К уменьшается (см. решение предыдущей задачи). Как будет изменяться ∆rS0 в этой реакции при повышении температуры? Выведите уравнения зависимости ∆rS0 (T).
Решение. В области температур, где нет фазовых переходов изменения энтропии в зависимости от температуры описывается уравнением
S0(T)
= S0(298)
+
,(3.4)
где Cp(T) описывается полиномом вида:
Cp(T)
= a
+
bT
+
,
Коэффициенты которого, так же как и S0(298), табулированы [1].
Для химической реакции зависимость ∆rS0(T) описывается уравнением:
∆rS0
(T)
=
∆rS0(298)
+
,(3.4)
∆rCp(T)
= ∆a
+
∆bT
+
,
Разумеется, в температурном интервале 298 – T фазовые переходы отсутствуют.
Рассмотрим вначале, как изменяется с температурой ∆rS0 (T).
Необходимые для расчета данные [1] оформим в виде матрицы термодинамических характеристик и вектора – столбца стехиометрических коэффициентов.
Вещество Al2O3 (тв) + 3SO3(газ) → Al2(SO4)3(тв)
И, подставив полученные результаты в (3.4):
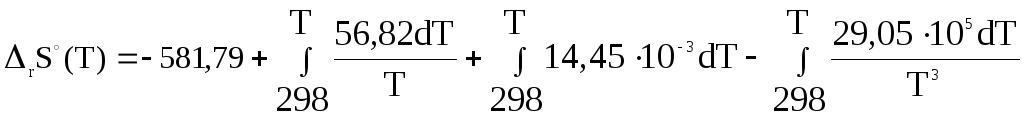
После интегрирования:
Полученная
зависимость оценивает изменение
в
интервале температур 298 – 1100 К.
Рассчитаем,
используя полученную зависимость,
при
увеличении температуры в этом интервале:
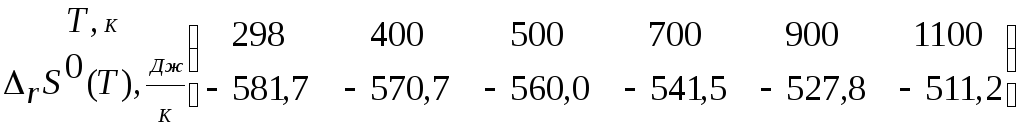
Полученные
результаты свидетельствуют о том, что
при
увеличении температуры увеличивается.
Возникает
естественный вопрос: чем вызван такой
характер изменения 
и
всегда ли наблюдается подобный эффект?
В соответствии с (3.3)
и
изменение энтропии при повышении
температуры определяется знаком 
.
В рассматриваемом случае
и
при любой T
рассматриваемого интервала 
подтверждает
расчет, данные которого приведены в
таблице:
|
T, K |
298 |
400 |
500 |
700 |
900 |
1100 |
|
|
28,3 |
44,4 |
52,4 |
61,0 |
66,2 |
70,3 |
,Дж/КРезультаты иллюстрируются рис.
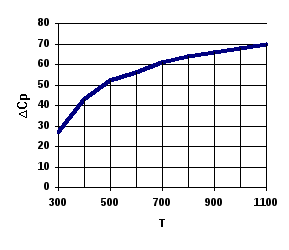
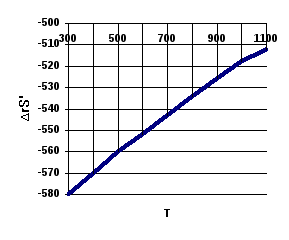
Рис.
Влияния температуры на
и
в реакции
Al2O3 (тв) + 3SO3(газ) → Al2(SO4)3(тв)
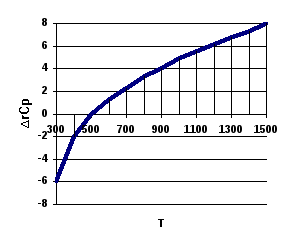
Разумеется, согласно (3.3), могут быть и более «хитрые» варианты.
Так, например, для реакции
З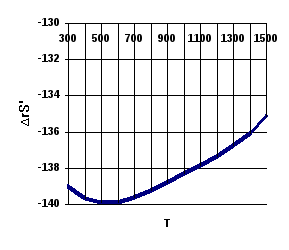
ависимость
и
изображены
на рис.
Рис.
Изменение
и
в
зависимости
от температуры в реакции 
В этом случае
зависимость
проходит
через минимум при Т=500К, что обусловлено
изменением знака
при
этой температуре.
Подтвердим приведенные данные расчетом:
Вещество
Параметр.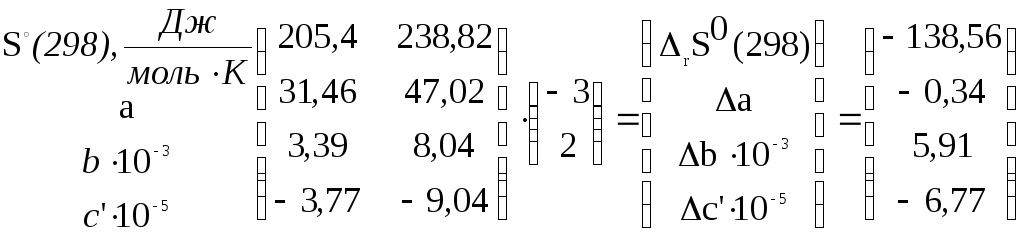
Тогда
и согласно (3.3)
И после интегрирования:
Расчет
значений
и
в
температурном интервале 298-1500 К по
полученным соотношениям приведен в
таблице:
|
T,K |
298 |
400 |
500 |
700 |
900 |
1100 |
1300 |
1500 |
|
|
-6,2 |
-2,1 |
-0,09 |
2,4 |
4,1 |
5,6 |
6,9 |
8,0 |
|
|
-138,6 |
-139,8 |
-140,0 |
-139,6 |
-138,8 |
-137,8 |
-136,8 |
-135,7 |
