Класс функций, сохраняющих единицу (к1).

Если булева функция на единичном наборе <111…1> аргументов равна единице, то говорят, что эта функция сохраняет единицу:

f(111…1)=1.

Так как на одном наборе <11..1> значение функции зафиксировано, то остается 2ⁿ-1 независимых наборов, т.е. число функций, сохраняющих единицу, равно половине от всех функций n переменных, т.е. .

Пример. n=2. Класс К₁ содержит:

f₁(xy), f₃(xy) , f₅(xy) , f₇(xy) , f₉(xy) , f₁₁(xy) , f₁₃(xy) , f₁₅(xy).

Теорема. При суперпозиции переключательных функций, сохраняющих 1, и при подстановке в эти функции других переменных получаются функции, сохраняющие 1, и только они.

Класс монотонных булевых функций (м).

Переключательная функция называется монотонной, если при любом возрастании набора значения этой функции не убывают.

Число функций класса М оценивается асимптотически:

≤ φ_n ≤ ,

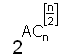где φ_n – число монотонных функций от n аргументов; А– некоторая константа.

Пример. n=2. Класс М содержит

f₀(xy), f₁(xy) , f₃(xy) , f₅(xy) , f₇(xy) , f₁₅(xy).

При суперпозиции монотонных булевых функций и при подстановке в эти функции переменных получаются монотонные функции и только они. Имеем монотонные функции:

f₁(x₁ x₂ … x_n);

φ₁(y₁ y₂ … );

. . . . . . .

φ_n(y₁ y₂ … ).

Пусть f₂(y₁ y₂ … )= f₁(φ₁,φ₂, …,φ_n).

Зафиксируем значение функции f₂ на некотором наборе < y₁ y₂ … >, а затем увеличим этот набор. При этом значение любой монотонной функции φ_i<y₁y₂… > уменьшиться не может, отсюда следует, что набор аргументов функции f₁ не уменьшится с увеличением набора функции f₂, а, следовательно, и значение функции f₂ не уменьшится. Аналогично будет при подстановке аргументов.

Класс самодвойственных функций (u).

Переключательная функция называется самодвойственной, если на каждой паре противоположных наборов она принимает противоположные значения:

или, что то же самое,

Пример. n=2. Класс U содержит

f₃(xy) , f₅(xy) , f₁₀(xy) , f₁₂(xy).

При суперпозиции самодвойственных переключательных функций и при подстановке в эти функции переменных получаются самодвойственные функции и только они.

Имеем самодвойственные функции

f₁(x₁ x₂ … x_n);

φ₁(y₁ y₂ … );

. . . . . . .

φ_n(y₁ y₂ … ).