Алгоритм построения.

Чтобы булеву функцию, заданную таблицей значений или любым другим способом, представить в виде многочлена, достаточно:

1. записать функцию в виде суммы по mod 2 минтермов, равных единице на тех же наборах, на которых равна заданная функция;

2. все аргументы, входящие в полученное выражение в инверсной форме, заменить с помощью соотношения ;

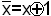3. раскрыть скобки и сделать приведение подобных членов с учетом тождества:

x, если n нечетно;

0, если n четно.

N

Пример. Представить в виде многочлена функцию f₁₄(AB):

f₇(AB)= m₀+m₁+m₂= m₀ m₁ m₂=

Пример. Представить в виде многочлена функцию f₉(AB):

f₉(AB)= m₀+m₃= m₀ m₃=

.

На базе функции 1, /\ и строится алгебра Жегалкина, но по своим свойствам она более близка к обычной алгебре и отличается от последней лишь тем, что логическое сложение заменено сложением по mod 2.

§7. Основные классы функций алгебры логики.

Рассмотрим пять классов булевых функций, которые называются замечательными классами, так как функции, принадлежащие к этим классам, обладают следующими свойствами: любая булева функция, полученная с помощью операций суперпозиции и подстановки из функций одного класса, обязательно будет принадлежать к тому же классу.

Напомним, что подстановкой называется замена одних аргументов функции другими или изменение порядка записи аргументов; суперпозицией называется подстановка в функцию вместо ее аргументов других функций.

Класс линейных функций от n аргументов (Ln).

В соответствии с теоремой Жегалкина любая булева функция представлена в виде полинома.

Булева функция называется линейной, если она может быть представлена полиномом первой степени, т.е. записана в виде

f(x₁ x₂ … x_n)= α₀ α₁ x₁ α₂ x₂ … α_n x_n,

где α₀, α₁, … , α_n – коэффициенты, равные 0 или 1.

Число различных линейных функций n переменных равно числу различных наборов вида <α₀ α₁ … α_n > и равно 2ⁿ⁺¹.

Пример. n=2. Класс L₂ состоит из 8 функций:

f₀(xy)=0; f₃(xy)=x; f₅(xy)=y;

f₆(xy)= ; f₉(xy)=1 x y;

f₁₀(xy)=1 y; f₁₂(xy)=1 x; f₁₅(xy)=1.

Отметим, что переключательные функции одного аргумента все линейны:

L₁: f₀(x)=0, f₁(x)=x, f₂(x)=1 x, f₃(x)=1.

Теорема. При суперпозиции линейных функций и при подстановке в эти функции других переменных получаются линейные переключательные функции и только они.

Дано f₁(x₁ x₂ … x_n)= α₀ α₁ x₁ … α_n x_n;

φ₁(y₁ y₂ … )= b₁₀ b₁₁ y₁ … ;

φ₂(y₁ y₂ … )= b₂₀ b₂₁ y₁ … ;

. . . . . . . . . . . . . . . . . . . .

φ_n(y₁ y₂ … )= b_n0 b_n1 y₁ … ,

Подставим φ_i вместо x_i функции f₁ , получим выражение f₂, в котором постоянные коэффициенты умножаются на линейные функции. Приведя подобные члены, получим представление функции f₂ в виде линейного полинома.

Пример. f₁(x₁ x₂ x₃)=1 x₁ x₂ x₃;

x₁=φ₁(y₁ y₂ y₃ y₄)= y₁ y₃ y₄;

x₂=φ₂(y₁ y₂)= 1 y₁ y₂;

x₃=φ₃(y₁ y₂ y₃ y₄)= 1 y₁ y₂ y₃ y₄;

f₂(y₁ y₂ y₃ y₄)= 1 φ₁(y₁ y₂ y₃ y₄) φ₂(y₁ y₂) φ₃(y₁ y₂ y₃ y₄)=

=1 y₁ y₃ y₄ 1 y₁ y₂ 1 y₁ y₂ y₃ y₄=1 y₁.

При любых подстановках x_i функция остается линейной.

Из линейных функций нельзя получить нелинейную, а наоборот можно.

Класс функций, сохраняющих нуль (К₀).

Если функция на нулевом наборе аргументов <00…0> равна нулю, то говорят, что функция сохраняет нуль:

f(000…0)=0.

При фиксированном n число таких функций составляет половину всех булевых функций n аргументов, т.е. .

Пример. n=2. В класс К₀ входят следующие функции:

f₀(xy), f₁(xy) , f₂(xy) , f₃(xy) , f₄(xy) , f₅(xy) , f₆(xy) , f₇(xy).

При суперпозиции переключательных функций, сохраняющих нуль, и при подстановке в эти функции других переменных получаются переключательные функции, сохраняющие нуль и только они.

Пусть имеем

f₁(x₁ x₂ … x_n), φ₁(y₁ y₂ … ), …, φ_n(y₁ y₂ … ).

Все эти функции сохраняют нуль на нулевом наборе. Подставив вместо x_i функции φ_i, получим новую функцию

f₂(y₁ y₂ … )= f₁(φ₁,φ₂, …,φ_n ).

Найдем значение f₂ на нулевом наборе:

f₂ (00 …0)= f₁ (000 …0)=0.

Так как на нулевом наборе все аргументы равны нулю, то любая подстановка этих аргументов не изменит значение функции.