§4. Выражение функции в сднф и скнф с помощью аналитических преобразований.

Для получения СДНФ функции аналитическим способом используется следующий прием:

1. аналитическое выражение функции приводится к бесскобочной записи в форме дизъюнкции каких-либо конъюнкций;

2. каждая конъюнкция, имеющая число сомножителей меньше n, умножается на выражение «1» через все недостающие переменные ( );

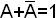3. раскрываются скобки и приводятся подобные члены.

Пример. Найти СДНФ функции f(ABCD)= .

m₁₅ + m₁₄ + m₁₃ + m₁₂ + m₁₁ + m₉ + m₈ + m₃ +m₁.

Для получения СКНФ функции без использования табличной записи следует применять процедуру вида:

1. аналитическое выражение функции приводится с помощью соотношения AB+C=(A+C)(B+C) к конъюнктивной записи со скобками, причем в скобках должны стоять дизъюнкции отдельных переменных в прямой или инверсной форме;

2. к каждой дизъюнкции добавляется выражение 0 через все недостающие переменные ( );

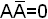3. вновь используется дистрибутивный закон вида и приводятся подобные члены.

Пример. Найти СКНФ функции

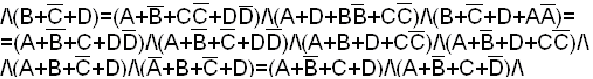
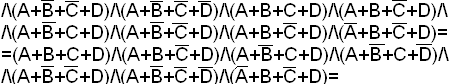
=М₁₅ М₁₃ М₁₁ М₁₀ М₉ М₈ М₅

Рассмотрим расширение сокращенной записи элементарного произведения до суммы минтермов.

Пусть , представим данную запись в виде

A B C D

- - 0 1

Затем, не меняя значений известных цифр в записи индекса минтерма, подставляем все возможные комбинации цифр соответствующих разрядов:

0 0 0 1

0 1 0 1

1 0 0 1

1 1 0 1

Полученные цифры соответствуют индексам минтермов, содержащихся в СДНФ исходной функции, т.е.

f(ABCD)=m₁+m₅+m₉+m_13.

§5. Способы выявления равносильности булевых функций.

Как табличная запись функции, так и запись функции в СДНФ и в СКНФ являются единственными, поэтому для доказательства равносильности булевых функций используются следующие способы:

1. Сравнение табличных записей функций по всем возможным наборам переменных.

Пример. Доказать тождество f₂₄₈(ABC)= (табл. 9,10).

Таблица 9 Таблица 10

A B C f₂₄₈(ABC) A B C B↓C

0 0 0 1 0 0 0 1 0 1

0 0 1 1 0 0 1 0 1 1

0 1 0 1 0 1 0 0 1 1

0 1 1 1 0 1 1 0 1 1

1 0 0 1 1 0 0 1 0 1

1 0 1 0 1 0 1 0 1 0

1 1 0 0 1 1 0 0 1 0

1 1 1 0 1 1 1 0 1 0

248=128+64+32+16+8=2⁷+2⁶+2⁵+2⁴+2³=11111000₂.

Так как значение функций на всех наборах совпадает, то f₂₄₈(ABC)= и тождество доказано.

Способ доказательства равносильности функций по таблицам очень нагляден, но при большом числе n затруднителен.

2. Сравнение СДНФ и СКНФ функций.

Пример. Доказать тождество f₁₉₆(ABC)= ;

196₁₀=128+64+4=2⁷+2⁶+2²=11000100₂.

В индексе функции единиц меньше, чем нулей, следовательно, СДНФ функции имеет более короткую запись, чем СКНФ:

f₁₉₆(ABC)= m₀+m₁+m₅;

= m₀+m₁+m₅.

СДНФ функций совпадают, следовательно, тождество доказано.

Пример. Доказать тождество

F₂₃₇(ABC)= ;

237₍₁₀₎=128+64+32+8+4+1=2⁷+2⁶+2⁵+2³+2²+2⁰=11101101₍₂₎,

так как нулей мало, используем СКНФ:

f₂₃₇(ABC)= М₄ М₁ ;

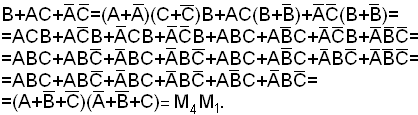
СКНФ функций совпадают, тождество доказано.

3. Преобразование одной из сравниваемых функций с помощью основных соотношений до полного совпадения с другой. Этот способ не поддается алгоритмизации, и поэтому, если не удалось привести функции к одному виду, то еще нельзя утверждать, что эти функции неравносильны.

Пример. Доказать тождество ;

Тождество доказано.