Диаграммы Венна.

Наглядная интерпретация основных соотношений булевых переменных представлена на диаграммах Венна.

Класс булевых переменных определяется как класс, включающий все области внутри квадрата (рис.1).

рис.1.

Любой элемент А этого класса представлен областью, ограниченной замкнутой кривой. - совокупность точек квадрата, не входящих в область А.

Здесь 0 представлен как класс, совсем не имеющий точек, а 1 – как класс всех точек квадрата.

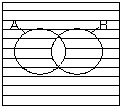
А+В – наименьшая область, содержащая одновременно А и В.

АВ – наибольшая область, содержащаяся одновременно и в А, и в В. Диаграм-мы Венна для элементарных булевых функций изображены на рис.2:

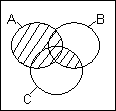
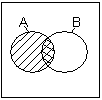
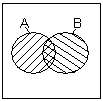
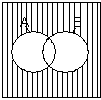
а) б) в) г) д) рис.2.

§2. Формы записи булевых функций. Табличная запись.

Одним из распространенных способов записи булевой функции является ее задание с помощью таблицы соответствия (таблицы истинности), которая сопоставляет всем двоичным наборам аргументов значения функции на этих наборах. Буквы и наборы в таблице могут располагаться в любом порядке, однако практически целесообразно осуществлять запись следующим образом:

порядок записи букв в таблице совпадает с порядком аргументов в записи функции;
наборы, представляющие собой двоичные числа, располагаются в таблице в порядке их возрастания. Каждому набору приписывается номер соответственно представляемому им числу:

000…00 – нулевой набор;

000 …01 – 1-й набор;

. . . . . . . . . . . . . . . . . . .

111 … 11 - (2ⁿ-1)–й набор.

Функция, записанная в табличном виде, имеет индекс, равный двоичному числу, образованному значениями этой функции, записанными слева направо, начиная со значения на нулевом наборе.

Пример. Запись функции f₂₄₈(АВС) = приведена в табл.5.

Таблица 5.

A B C B↓C

0 0 0 1 0 1

0 0 1 0 1 1

0 1 0 0 1 1

0 1 1 0 1 1

1 0 0 1 0 1

1 0 1 0 1 0

1 1 0 0 1 0

1 1 1 0 1 0

При задании булевых функций при 3≤n≤10 иногда используют прямоугольные таблицы, т.е. те же таблицы соответствия, но в несколько ином начертании, позволяющем получить более компактную запись. Для функции от n переменных такая таблица имеет строк и столбцов, где - целая часть числа n/2.