Макроячейка.

Макроячейка, внутренняя структура которой приведена на рис. 4.15, содержит:

• участок локальной программируемой матрицы "И";

• программируемую матрицу распределения термов;

• матрицу "ИЛИ";

• программируемый элемент сложения по mod2;

• синхронный триггер;

• параллельный логический расширитель;

• разделяемый логический расширитель;

• цепь быстрого ввода;

• набор программируемых мультиплексоров (MS[3...1]).

от вывода Цепь быстрого ввода СБИС

кБВВ

вПМС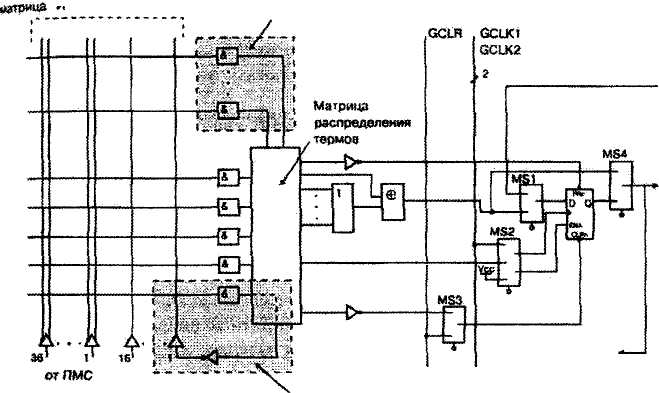

Лкальная

Программируемая

"

Параллельные логические расширители

Разделяемый логический расширитель

Рис. 4.15 Структура макроячейки

Комбинационную часть макроячейки образуют: участок локальной программируемой матрицы "И", обеспечивающий формирование пяти термов; программируемая матрица распределения термов, позволяющая размещать формируемые термы и использовать параллельный и разделяемый логические расширители; матрица "ИЛИ"; элемент сложения по mod2; параллельный расширитель; разделяемый расширитель.

Параллельный расширитель.

Для реализации сложных логических функций, в ДНФ которых входит более пяти термов, целесообразно применение параллельных логических расширителей, позволяющих совместно использовать термы (либо все, либо оставшиеся нераспределенными) смежных макроячеек. Одна цепочка параллельных расширителей может включать до четырех макроячеек, обеспечивая, таким образом, возможность реализации логической функции, имеющей до двадцати термов.

Организация цепочки параллельных расширителей иллюстрируется на рис. 4.16.

В пределах каждого Л Б, содержащего 16 макроячеек, может быть организовано две цепочки параллельных расширителей: одна на макроячейках с номерами от 1 до 8, другая на макроячейках с номерами от 9 до 16. При этом каждая из них начинается с макроячейки, имеющей меньший номер.

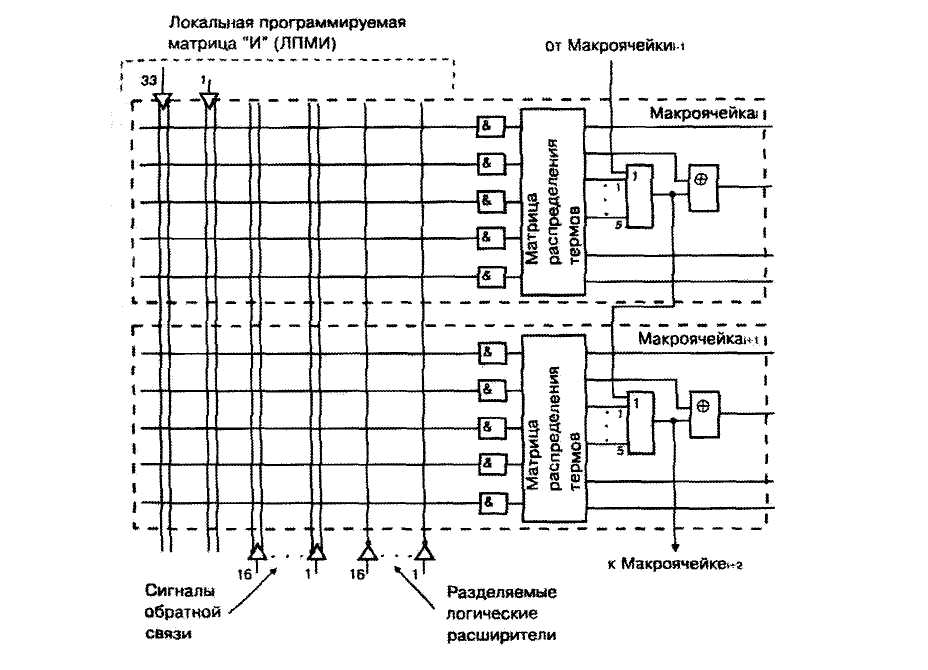
Рис. 4.16 Организация цепочки параллельных расширителей

Задержка в формировании выходного значения логической функции, в ДНФ которой входит 20 термов, реализованной с использованием параллельных

расширителей на СБИС МАХ 7032-5, составит: г = i_MD +3 * т_РЕХР ⁺ Т_с.омв =1.5+3*0.8+0.8=4.7нс, где: f_LAD -задержка формирования выходного сигнала матрицами "И", "ИЛИ";

Т_РЕХР - задержка распространения сигнала в цепи параллельного логического расширителя (от выхода матрицы "ИЛИ" i-ой макроячейки до выхода матрицы "ИЛИ" 0+1)-ой макроячейки); Тсомв " задержка передачи сигнала с выхода матрицы "ИЛИ" на выход макроячейки.

Разделяемый расширитель.

Для реализации сложных логических функций с большим количеством переменных, целесообразно использование разделяемых логических расширителей. Разделяемый логический расширитель формирует терм, инверсное значение которого передается матрицей размещения термов в локальную программируемую матрицу "И" и может быть использовано в любой макроячейке данного ЛБ.

Отметим, что каждая макроячейка содержит только один разделяемый расширитель.