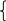Глава 3. Структурный и абстрактный синтез устройств вм.

Структурный синтез операционных устройств ВМ. Операционное устройство ВМ можно представить состоящим как бы из двух частей — комбинационной и памяти. На входы комбинационной части поступают сигналы с выходов элементов памяти (триггеров) Q₁, …, Q_m, а также сигналы, приходящие по шинам управления x₁, …, x_m. Назначение шин управления состоит в том, чтобы из всех микроопераций, выполняемых устройством, выбрать одну, требуемую в данный момент. Сигналы с выходов комбинационных схем подаются на входы триггеров. Функция возбуждения входного i-го триггера записывается в следующем виде:

.

Значения всех переменных в этом выражении определены для одного и того же момента времени t, поэтому функции возбуждения триггеров являются переключательными функциями, которым соответствуют комбинационные схемы, формирующие входные сигналы для триггеров. Следовательно, если известен тип триггера, то задача структурного синтеза устройства заключается в составлении функции возбуждения каждого триггера, функции кодирования выходов заданного устройства и минимизации. При выполнении структурного синтеза используются матрицы переходов триггеров (табл. 3.1), где для каждого типа триггера указаны значения входных сигналов, определяющие переход триггера из одного состояния в другое. Если значение входного сигнала не влияет на данный переход, то в матрице указывается неопределенный коэффициент b. Для триггера D — V–типа дополнительно указан второй коэффициент по управляющему входу.

Таблица 3.1

Переходы	Тип триггера
0 – 0	0	b	0	b	b a	b	1	b	0
0 – 1	1	b	1	1	1	1	0	0	1
1 – 0	b	1	0	0	1	0	1	1	0
1 – 1	b	0	1	b	b a	1	b	0	b

Алгоритм структурного синтеза

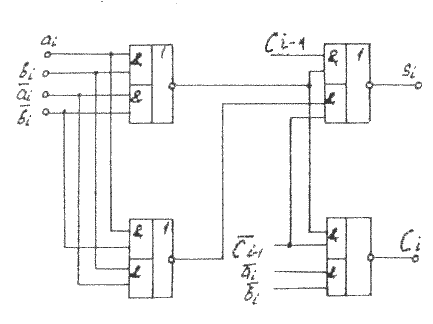
1. Определяется необходимое число независимых шин управления. Число управляющих шин зависит от числа микроопераций, выполняемых устройством, и находится из соотношения 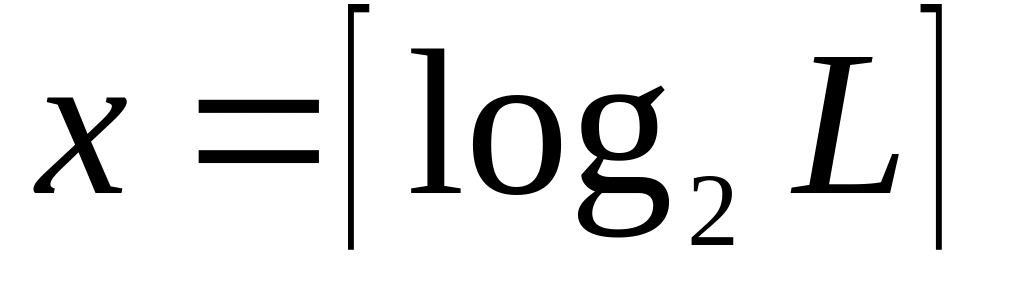, где L — число микроопераций.

2. По числу различных состояний N устройства определяется необходимое количество триггеров: m 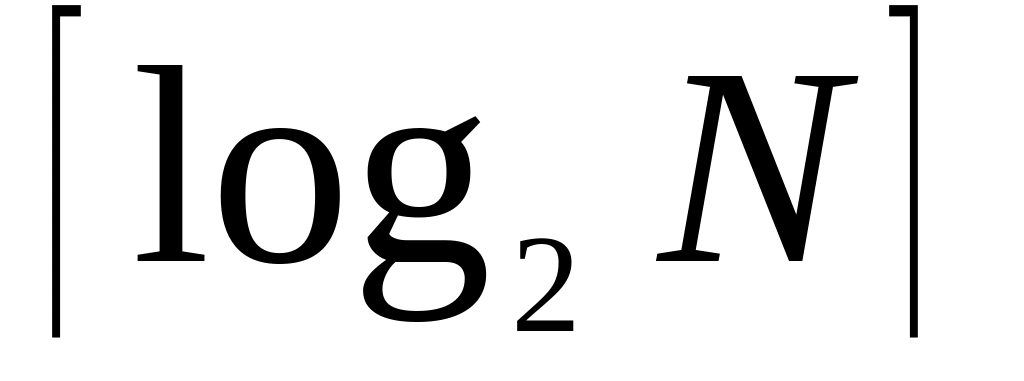, каждое состояние устройства кодируется m-разрядным двоичным кодом, i-й разряд соответствует выходному сигналу i-го триггера.

3. Кодируется внутреннее состояние синтезируемого автомата.

4. Согласно закону функционирования составляется кодированная таблица выходов устройства и переходов из одного состояния в другое при определенных входных воздействиях. Поскольку устройство представляет совокупность триггеров, такая таблица будет включать функции возбуждения всех входов триггеров возбуждения.

5. Выбирается (или задается) тип каждого триггера, по таблице переходов или матрице переходов составляются таблицы функций возбуждения всех входов каждого триггера.

6. Полученные функции возбуждения и функции выходов минимизируются соответствующим выбором значений неопределенных коэффициентов.

7. Согласно функциям возбуждения и в соответствии с выбранной (заданной) элементной базой строится структурная схема.

Синтез микропрограммных автоматов. Управляющий автомат, реализующий микропрограмму работы дискретного устройства, принято называть микропрограммным автоматом. Его синтез состоит из следующих этапов:

1. Составление частных содержательных микропрограмм выполнения операции автомата.

2. Построения частных микропрограмм с учетом отметок граф-схемы алгоритма символами.

3. Получение отмеченных частных микропрограмм.

4. Построение графов частных управляющих автоматов Мили или Мура.

5. Построения графа многофункционального автомата Мили или автомата Мура путем объединения состояний автоматов и введения настроечного алфавита.

6. Структурный синтез.

Далее составляется таблица переходов микропрограммного автомата. Для автомата Мили таблица содержит четыре столбца: a_m и a_s — исходное состояние и состояние перехода; х(a_m, a_s) — конъюнкция переменных из множества х, принимающая значение 1 на данном переходе; у(a_m, a_s) — подмножество выходных переменных, принимающих значение 1 на данном переходе. Каждая строка таблицы переходов соответствует одному пути перехода, т.е. дуге графа автомата с одним входным и одним выходным сигналами.

Таблица переходов микропрограммного автомата Мура содержит три столбца. В ней выходные сигналы из множества у(a_m) записываются в столбце a_m рядом с состоянием, в котором они формируются.

С помощью минимизации числа строк таблицы переходов автомата и методов доопределения функций строится логическая схема автомата, являющаяся совместной реализацией функций возбуждения функций выходов.

Абстрактный синтез автоматов. Задача абстрактного синтеза заключается в составлении таблиц переходов и выходов автомата по заданным условиям его функционирования.

Абстрактный синтез автоматов включает два этапа. Первый этап состоит в получении таблиц переходов и выходов в некоторой исходной форме. На втором этапе проводится минимизация количества внутренних состояний заданного автомата.

Алгоритм абстрактного синтеза заключается в следующем. Фиксируется начальное состояние a₀ и для входного слова l_i, состоящего из r букв, назначается r внутренних состояний автомата a_i1, a_i2, …, a_ir. Переходы в автомате назначаются так, что первая буква слова l_i переводит автомат из состояния a₀ в состояние a_i1, вторая буква — из состояния a_i1 в состояние a_i2 и т.д. Аналогичные последовательности внутренних состояний назначаются для всех остальных слов. Затем все конечные состояния a_ir, в которые автомат попадает после подачи слов, входящих в событие S_j, отмечаются выходным сигналом у_i.

Чтобы система переходов автомата была определенной для всех слов, имеющих одинаковые начальные отрезки, следует назначать одну и ту же последовательность состояний. В состояниях, не отмеченных буквами выходного алфавита у₁, …, у_k, а также в начальном состоянии автомат должен выдавать пустую букву, соответствующую событию S_k+1. Для запрещенного события последовательность состояний можно не назначать.

При абстрактном синтезе целесообразно использовать следующие соотношения:

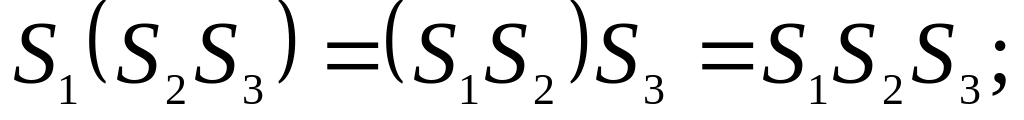
Алгоритм минимизации числа внутренних состояний автомата включает следующие действия:

1. Все внутренние состояния разбиваются на группы, количество которых равно количеству выходных сигналов автомата. Если существует такое состояние, в котором автомат выдает пустое слово, то такие состояния также выделяют в общую группу.

2. По таблице переходов автомата определяют, к каким группам принадлежат внутренние состояния, в которые автомат переходит из данного состояния под воздействием каждой буквы входного алфавита.

3. Проводится новое разделение внутренних состояний на группы, при этом объединяются в каждой группе состояния, отмеченные одинаковой последовательностью букв.

4. Пользуясь таблицей переходов автомата, снова отмечаются каждые состояния последовательности букв. Объединение состояний в группы продолжается до тех пор, пока новые группы состояний появляться не будут.

рис. 3.1

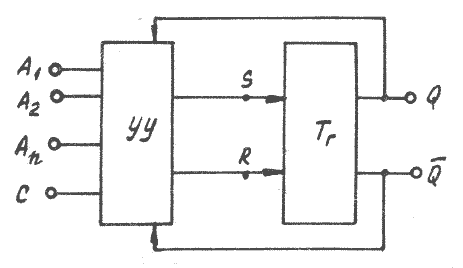
Триггерные устройства. Основными элементами, предназначенными для хранения информации, являются устройства с двумя устойчивыми состояниями — триггеры. Структуру триггера можно представить в виде запоминающего элемента и схемы управления (рис 3.1).

Запоминающий элемент имеет два выхода Q и , разрешенные сигналы на которых всегда противоположны, и два входа s (set – установка) и r (reset – сброс). Переключающий сигнал по входу s устанавливает запоминающий элемент в состояние «1», а по входу r — в состояние «0». В общем случае запоминающий элемент может иметь несколько установочных входов.

Схема управления преобразует информацию, поступающую на входы А₁…А_n, в сигналы, которые подаются на установочные входы запоминающего элемента. Как правило, триггеры имеют еще один вход — вход для синхронизирующих сигналов С. Сигналы, поступающие на этот вход, определяют момент приема триггером входной информации. Поскольку прием информации синхронизирован с моментом подачи сигнала на вход С, то такой триггер назван синхронизируемым, или синхронным.

Рассматриваемые ниже триггеры обладают следующими свойствами. На входы А₁…А_n поступают сигналы, несущие логическую входную информацию, на вход С — сигнал синхронизации. Входная информация принимается на хранение триггером с поступлением сигнала синхронизации или изменением его фронта. Такой режим соответствует синхронной работе триггера. Но синхронный триггер может применяться и при асинхронной работе. При этом на синхронизирующий вход триггера сигналы могут поступать от схем, непосредственно не связанных с синхронизирующими сигналами.

Наряду с хранением информации триггер может выполнять различные логические функции. Логические свойства триггера можно описать с помощью таблицы переходов (табл. 3.2), которая Q(t+1) определяет зависимость выходных сигналов триггера от значений входных сигналов A_i(t) и состояния триггера Q(t) в предыдущий момент времени. Для каждого типа триггера, задаваемого таблицей переходов, вводят специальное обозначение входов, отличное от общего обозначения А.

Таблица 3.2а. Таблица переходов триггера D

Вход (время t)	Выход (время t+1)
0	0
1	1

Таблица 3.2б. Таблица переходов триггеров J-K, R -S,

Входы (время t)		Выход (время t+1)
0	0	Q(t)	Q(t)	-
0	1	1	1	0
1	0	0	0	1
1	1		-
R, , K	S, , J	J-K	R-S

Рассмотрим наиболее часто применяемые типы триггеров.

D – триггер имеет один логический вход D (delay – задержка), состояние которого с каждым синхронизирующим сигналом передается на выход, т.е. выходные сигналы представляют собой задержанные входные. Таким образом, D – триггер — элемент задержки входных сигналов на один такт. Характеристическое уравнение триггера Q(t+1)=D(t).

J-K – триггер имеет два логических входа: j и k. Сигнал по входу j(j=1) устанавливает триггер в единичное состояние, а по входу k(k=1) в нулевое состояние. Если j=k=1, то триггер изменяет свое состояние на противоположное; при одновременной подаче на входы сигналов j=k=0 триггер не изменяет своего состояния. Характеристическое уравнение триггера .

R-S – триггер имеет два логических входа: R и S. Одновременная подача на оба входа триггера сигналов, соответствующих единице, запрещена. Если на оба входа поданы сигналы, соответствующие нулю, то триггер на изменяет своего состояния. Характеристическое уравнение триггера .

Обычно триггер, управляемый по синхронному входу, кроме информационных входов А имеет, как правило, асинхронные входы предварительной установки триггера в состояние «0» или «1». Сигналы, поступающие на эти входы, пользуются приоритетом, т.е. независимо от состояния других входов триггера они сразу (по переднему фронту) устанавливают триггер в определенное состояние. Буквой обозначают асинхронный вход для установки триггера в состояние «1», а буквой — для установки триггера в состояние «0». Синхронный триггер имеет обычно инверсные установочные входы и реализует функцию, приведенную в таблице переходов (см. табл. 3.2, б). Синхронные триггеры с асинхронными и установочными входами получили название универсальных триггеров соответствующего типа.

Синтез триггерных устройств. Универсальные триггеры классифицируются по способу их построения на два основных типа: основной — вспомогательный (M – S) со срабатыванием по заднему фронту сигнала синхронизации и основной — коммутирующий (М – К) со срабатыванием по переднему фронту сигнала синхронизации. Исходными данными при разработке триггера служат заданные описания его логического функционирования и требования к основным электрическим параметрам. Общая методика синтеза триггерных устройств следующая:

1. Составление таблицы переходов. Функционирование триггера может быть задано в различной форме: словесным описанием, в виде временных диаграмм, таблицами состояний и т.п. Входной алфавит определяется типом проектируемого триггера, а выходной алфавит и функции выходов выбираются двоичные. При структурном проектировании в качестве исходной информации о функционировании триггера используют таблицы переходов.

2. Составление кодированной таблицы прямых выходов триггера и его функций возбуждения, исходя из заданного типа базового триггера и кодирования его внутренних состояний.

3. Минимизация полученных функция возбуждения и выходов.

4. Составление структурной схемы на основании минимальных функций возбуждения и выходов в соответствии с выбранной элементной базой.

5. Составление электрической схемы триггера.

Синтез M – S-триггера. При синтезе M – S-триггеров с некоторыми ограничениями можно применить общую теорию конечных автоматов. Входной алфавит определяется типом проектируемого триггера, а выходной алфавит и функции выходов — двоичные. Для такого триггера закодированные внутренние состояния (S_i) автомата приведены в табл. 3.3, 3.4.

Таблица 3.3.

Si	M	S
S0	0	0
S1	0	1
S2	1	0
S3	1	1

Таблица 3.4.

Pi	C	V	K
P0	0	0	0
P1	0	0	1
P2	0	1	0
P3	0	1	1
P4	1	0	0
P5	1	0	1
P6	1	1	0
P7	1	1	1

Таблица 3.5.

Pi	Si
	S0	S1	S2	S3
P0	S0	S0	S3	S3
P1	S0	S0	S3	S3
P2	S0	S0	S3	S3
P3	S0	S0	S3	S3
P4	S0	—	—	S3
P5	S0	S1	—	S1
P6	S2	—	S2	S3
P7	S2	—	—	S1

Таблицы переходов и синтез двухступенчатого триггера рассмотрим на примере синхронного J-K – триггера, собранного на базе бистабильных ячеек и логических схем И — НЕ. Закодированные слова, подаваемые на входы триггера, приведены в табл. 3.6. С помощью таблицы кодирования внутренних состояний и входных слов составляется таблица переходов синхронного триггера. При отсутствии синхросигнала (по его заднему фронту) происходит перезапись состояния первой ступени М-триггера во вторую ступень S-триггера. Если на вход С подается сигнал синхронизации, то перезапись по переднему фронту из М в S запрещается. Таким образом, входные слова Р₀…Р₃ оказывают на автомат одинаковое воздействие.

Прочерком в таблице переходов (табл. 3.5) обозначены избыточные состояния. Так, если автомат находится в состоянии S₁ или S₂, то слово Р₄ не может быть подано на вход, потому что не произошла перезапись из М в S. Длительность синхросигнала должна быть достаточной для того, чтобы произошла перепись информации из М в S, по той же причине на вход не попадаются слова: Р₅, если автомат находится в состоянии S₂; Р₆, если автомат находится в состоянии S₁; Р₇, если автомат находится в состоянии S₁ или S₂.

Таблица 3.6.

			Выходные сигналы				Функции возбуждения
C	J	K	Q1(t)	Q2(t)	Q1(t+1)	Q2(t+1)
0	x	x	0	0	0	0	b	1	b	1
			0	1	0	0	b	1	0	1
			1	0	1	1	1	b	1	0
			1	1	1	1	1	b	1	b
1	0	0	0	0	0	0	b	1	b	1
1	0	0	0	1	—	—	—	—	—	—
1	0	0	1	0	—	—	—	—	—	—
1	0	0	1	1	1	1	1	b	1	b
1	0	1	0	0	0	0	b	1	b	1
1	0	1	0	1	0	1	b	1	1	b
1	0	1	1	0	—	—	—	—	—	—
1	0	1	1	1	0	1	0	1	1	b
1	1	0	0	0	1	0	1	0	b	1
1	1	0	0	1	—	—	—	—	—	—
1	1	0	1	0	1	0	1	b	b	1
1	1	0	1	1	1	1	1	b	1	b
1	1	1	0	0	1	0	1	0	b	1
1	1	1	0	1	—	—	—	—	—	—
1	1	1	1	0	—	—	—	—	—	—
1	1	1	1	1	0	1	0	1	1	b

Однако допустима подача входного слова Р5, если автомат находится в состоянии S₁, и входного слова Р6, когда автомат находится в состоянии S₂, так как в этом случае М находится в нулевом состоянии.

По таблице переходов составляется кодированная таблица переходов и функций возбуждения J-K – триггера (таблица 3.6), по которой находятся функции возбуждения по каждому входу триггеров, при этом используются любые методы минимизации.

Функция возбуждения

; ; ;

или в базисе И—НЕ

;

; ;

Структурная схема J-K – триггера приведена на рисунке 3.2.

Рис. 3.2 J-K – триггер

Таблица 3.7 Таблица истинности схем И—НЕ5 и И—НЕ6

В 0 0 1 0 1 0 1 0 1 1 1 1

Универсальный триггер типа J-K собран по структуре M – S на схемах И—НЕ (рис. 3.2). Основной триггер М, собранный на И—НЕ₃ и И—НЕ₄, принимает входную информацию и переключается по переднему фронту сигнала С.

По заднему фронту сигнала С информация из основного триггера М переписывается во вспомогательный триггер S, собранный на схемах И—НЕ₇ и И—НЕ₈, где фиксируется состояние триггерного устройства. Триггер имеет встроенные трехвходовые логические схемы И по входам J и K.

Рассмотрим синхронный режим работы универсального триггера J-K при подаче на его входы J и K одновременно единичных сигналов. Будем считать, что триггер находится в нулевом состоянии, т.е. на его входах и на входы и постоянно поданы единичные сигналы.

При одновременном поступлении единичных сигналов J, K и С на всех входах схемы И—НЕ₁ (с учетом единичного сигнала ) будут присутствовать единичные сигналы, которые переключают схему в нулевое состояние. Это, в свою очередь приведет к переключению схемы И—НЕ₄ в единичное состояние. Единичный сигнал с выхода этой схемы поступает на одни из входов схемы И—НЕ₃, на другие ее входы подаются единичные сигналы с входа и с выхода схемы И—НЕ₂. Таким образом, оказывается, что на все входы схемы И—НЕ₃ поданы единичные сигналы, которые переключают схему в нулевое состояние, и на выходе основного триггера М записывается единичный сигнал. В этот момент на триггере М фиксируется информация, противоположная информации, содержащейся на триггере S. Перепись этой информации во вспомогательный триггер S при наличии синхронизирующего сигнала невозможна, так как на оба входа логических схем с инверсным входом И—НЕ₅ и И—НЕ₆ подаются одинаковые входные сигналы (на схему И—НЕ₅ — нулевые, на схему И—НЕ₆ — единичные), которые сохраняют на их выходах единичные состояния (работа логической схемы с инверсным входом поясняется табл. 3.7).

По окончании действия сигнала синхронизации состояние схемы И—НЕ₁ изменяется на единичное, схема И—НЕ₅ переходит в нулевое состояние, которое переключает схему И—НЕ₈ в единичное состояние. Единичный сигнал, поступающий на вход схемы И—НЕ₇, переключает ее в нулевое состояние.

Следовательно, схемы И—НЕ₅ и И—НЕ₆ служат устройством управления перезаписи информации из основного триггера М во вспомогательный триггер S. Задержка при переключении схемы из одного устойчивого состояния в другое составляет 4t_d.

При подаче сигнала только на вход С при условии, что на всех остальных входах подан сигнал единица, триггер работает в счетном режиме, т.е. аналогично вышеописанному режиму.

По асинхронным входам триггер управляется аналогично асинхронным входам триггера D–типа. Поступающий на вход синхронизации нулевой сигнал С=0 блокирует переключение основного триггера М, а входные нулевые сигналы или переключают только вспомогательный триггер S. На основе триггера J-K можно, применяя соответствующую коммутацию или используя дополнительные схемы, получить триггеры, выполняющие функции триггеров R-S, D и Т.

Синтез М – К триггера. Рассмотрим особенности структурного проектирования триггеров класса М – К на примере синхронизируемого фронтом D–триггера, используя элементы И—НЕ.

Закодированные входные слова, подаваемые на вход автомата, представлены в табл. 3.8.

Для кодирования четырех состояний достаточно двух переменных Q₁ и, однако выберем для кодирования внутренних состояний три переменные Q₁, Q₂, Q₃ (табл. 3.9). Состояние схемы закодируем таким образом, чтобы выход схемы Q соответствовал выходу схемы Q₁. При этом из четырех избыточных состояний два (S₁ и S₂) применены в качестве рабочих промежуточных состояний триггера. Пятое состояние используется промежуточным при переключении триггера из (3) → (2), а шестое — при переходе триггера из (1) → (4).

Таблица 3.8

Pi	C	D
P1	0	0
P2	0	1
P3	1	1
P4	1	0

Таблица 3.9

Si	Q1	Q2	Q3
S7	0	0	0
S6	0	0	1
S2	0	1	0
S1	0	1	1
S8	1	0	0
S4	1	0	1
S5	1	1	0
S3	1	1	1

Введение этих промежуточных состояний позволило исключить критические гонки между системами обратных связей на всех переходах триггера. При заполнении таблицы переходов (табл. 3.10) примем, что триггер переключается по переднему фронту С и одновременное изменение сигналов C и D запрещено. Запрещенное состояние обозначается прочерком. По таблице переходов составляется кодированная таблица переходов и функций возбуждения D–триггера (табл. 3.11).

Таблица 3.10

Pi	Si
	S1	S2	S3	S4	S5	S6
P1	S1	S1	S3	S3	—	—
P2	S1	S1	S3	S3	—	—
P3	S6	S2	S4	S4	—	S4
P4	S2	S2	S5	S4	S2	—
Q	0	0	1	1	—	—

Таблица 3.11

Q(t) – Q(t+1)
0 — 0	b 1
0 — 1	b 0
1 — 0	0 1
1 — 1	1 / b
	b / 0

Данные табл. 3.12 заносятся на карты Вейча и производится минимизация функций. В результате получаем следующие минимальные функции возбуждения: ; ; ; ; ; .

Реализованный по этим соотношениям триггер будет содержать цепи со статическим сбоем при некоторых переключениях сигналов. Для исключения статического риска необходимо заменить минимальные выражения и оптимальными и и ввести дополнительные третьи входы в элементы И — НЕ₂ и И — НЕ₃. Соединив между собой в соответствии с логическими выражениями основной и коммутирующий триггеры, получим схему D–триггера в базисе И — НЕ (рис. 3.3).

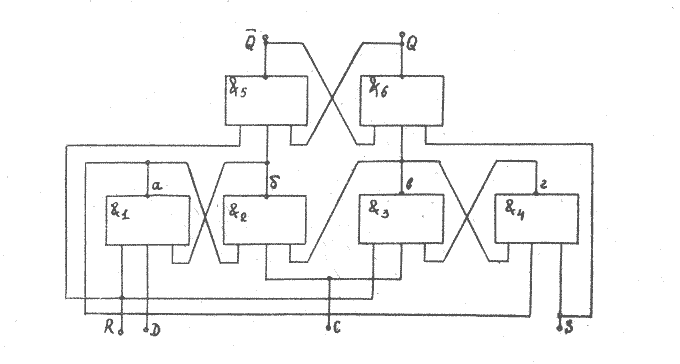
Рис. 3.3 D-триггер

Таблица 3.12

С	D	Значения выходных сигналов						Функции возбуждения
		Q1(t)	Q2(t)	Q3(t)	Q1(t+1)	Q2(t+1)	Q3(t+1)
0	0	0	0	0	—	—	—	—	—	—	—	—	—
		0	0	1	—	—	—	—	—	—	—	—	—
		0	1	0	0	1	1	b	1	1/b	b/0	b	0
		0	1	1	0	1	1	b	1	1/b	b/0	1/b	b/0
		1	0	0	—	—	—	—	—	—	—	—	—
		1	0	1	1	1	1	1	b	b	0	1/b	b/0
		1	1	0	—	—	—	—	—	—	—	—	—
		1	1	1	1	1	1	1	b	1/b	b/0	1/b	b/0
0	1	0	0	0	—	—	—	—	—	—	—	—	—
		0	0	1	—	—	—	—	—	—	—	—	—
		0	1	0	0	1	1	b	1	1/b	b/0	b	0
		0	1	1	0	1	1	b	1	1/b	b/0	1/b	b/0
		1	0	0	—	—	—	—	—	—	—	—	—
		1	0	1	1	1	1	1	b	b	0	1/b	b/0
		1	1	0	—	—	—	—	—	—	—	—	—
		1	1	1	1	1	1	1	b	1/b	b/0	1/b	b/0
1	1	0	0	0	—	—	—	—	—	—	—	—	—
		0	0	1	1	0	1	1	0	b	1	1/b	b/0
		0	1	0	0	1	0	b	1	1/b	b/0	b	1
		0	1	1	0	0	1	b	1	0	1	1/b	b/0
		1	0	0	—	—	—	—	—	—	—	—	—
		1	0	1	1	0	1	1	b	b	1	1/b	b/0
		1	1	0	—	—	—	—	—	—	—	—	—
		1	1	1	1	0	1	1	b	0	1	1/b	b/0
1	0	0	0	0	—	—	—	—	—	—	—	—	—
		0	0	1	—	—	—	—	—	—	—	—	—
		0	1	0	0	1	0	b	1	1/b	b/0	b	1
		0	1	1	0	1	0	b	1	1/b	b/0	0	1
		1	0	0	—	—	—	—	—	—	—	—	—
		1	0	1	1	0	1	1	b	b	1	1/b	b/0
		1	1	0	0	1	0	0	1	1/b	b/0	b	1
		1	1	1	1	1	0	1	b	1/b	b/0	0	1

Универсальный синхронный триггер типа D с инверсными установочными входами и функционирует согласно таблице переходов (табл. 3.13).

Таблица 3.13

Таблица переходов триггера D

Входные сигналы (время t)			Время Q(t+1)	Функция триггера
		С
0	0	0	—	Не определена
0	1	0	0	Уст. «0»
1	0	0	1	Уст. «1»
1	1	0	Q(t)	Хранение Q(t)
1	1	1	D(t)	Задержка D(t)

В отсутствие сигналов логического нуля на установочных входах данный триггер при С=0 не меняет своего состояния, при С=1 запоминает (задерживает) сигнал, поданный на управляющий вход D.

Схема триггера (рис3.3) реализована на элементах И—НЕ; запоминающий элемент образован на И—НЕ₅ и И—НЕ₆; остальные элементы составляют схему управления триггера с входными сигналами «б» и «в». Функции элементов И—НЕ: ; ; ; ; .

В асинхронном режиме нулевое значение синхросигнала С=0 приводит к отключению схемы управления (б=в=1) от запоминающего элемента, т.е. и . Работа триггера определяется только установочными сигналами:

при = =0 вызывает Q=1 и =1, т.е. схема функционирует неправильно;

при = =1 запоминающий элемент сохраняет прежнее состояние;

при =0 и =1 триггер либо сохраняет единичное состояние, либо переходит в него, если предыдущее состояние было нулевым;

при =1 и =0 триггер либо сохраняет нулевое состояние, либо переходит в него, если прежнее состояние было единичным (табл. 3.14). Время срабатывания триггера Т_тр=2τ_эл.

Таблица 3.14

Асинхронный режим триггера D

Время
t0	1	1	1	0
t1	0	1	0	1
t2	1	1	0	1
t3	1	0	1	0
t4	1	1	1	0
t5	0	0	1	1
t6	1	1	0 1	1 0

Состояние триггера в момент t₆ (при снятии запрещенных входных сигналов = =0) будет «0» или «1» в зависимости от случайных процессов в схеме. Временная работа триггера типа D приведена на рис. 3.4.

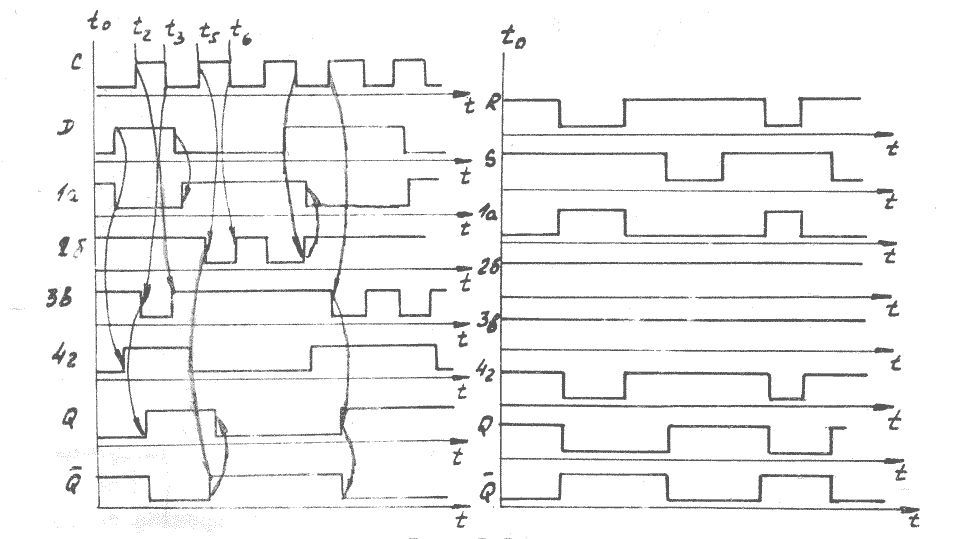
Рис. 3.4

В синхронном режиме на установочных входах рабочие сигналы отсутствуют: = =1 и функции элементов И—НЕ схемы имеют вид ; ; ; ; , т.е. состояние запоминающего элемента определяется сигналами «б» и «в» с выходов схемы управления. При отсутствии синхросигнала С=0 запоминающий элемент не меняет своего состояния; при наличии синхросигнала состояние триггера определяется ранее поданным сигналом управления по входу D (табл. 3.15).

Таблица 3.15

Синхронный режим триггера D

Время	D(t)	C(t)
t0	-	0	-	1	1	-	1	0
t1	1	0	0	1	1	1	1	0
t2	1	1	0	1	0	1	0	1
t3	1	0	0	1	1	1	0	1
t4	0	0	1	1	1	0	0	1
t5	0	1	1	0	1	0	1	0
t6	0	0	1	1	1	0	1	0

Время срабатывания триггера 3τ_эл.

При внешнем соединении инверсного выхода со входом D триггер реализует счетный режим по входу С, т.е. меняет свое состояние на противоположное по каждому входному сигналу (табл. 3.16).

Таблица 3.16

Счетный режим триггера D

Время	D(t)	C(t)	а	б	в	г	Q
t0	0	0	1	1	1	1	0
t1	1	1	1	0	1	0	1
t2	0	1	1	1	0	0	1
t3	1	1	0	1	0	1	0
t4	0	0	1	1	1	1	0

Регистры. Под регистром понимается операционное устройство для хранения, приема и выдачи кодов.

Регистр, предназначенный для работы с двоичными кодами, представляет собой совокупность триггеров, количество которых соответствует количеству разрядов в двоичном коде, и вспомогательных схем, позволяющих дополнительно реализовать следующие функции регистров:

запись нулевого кода;

сдвиг кода вправо или влево на заданное число разрядов;

прием – передачу с преобразованием последовательного кода в параллельный и наоборот.

При реализации последовательного кода все его разряды во времени передаются последовательно, один за другим по одной линии связи, при реализации параллельного кода всего его разряды передаются одновременно, каждый по своей цепи.

На рис. 3.5 представлена схема регистра на D-триггерах с приемом и выдачей параллельного кода слова и шиной установки нуля. Перед записью на регистр информации все триггеры предварительно сбрасываются в нуль, затем на установочные входы триггеров поступают одновременно сигналы разрядов двоичных слов. Передача информации с регистра может быть осуществлена прямым кодом (с прямых выходов триггеров) и обратным кодом (с инверсных выходов триггеров).

Выходную информацию с регистра можно также снять одновременно и с прямого, и с инверсного выхода каждого триггера, при этом каждый разряд кода передается одновременно по двум шинам) в зависимости от значения двоичного разряда на одной из них всегда присутствует сигнал единицы). Такой вид передачи называется передачей парафазного кода. Если парафазный код поступает на вход регистра, то цепь предварительного сброса регистра в нуль не используется.

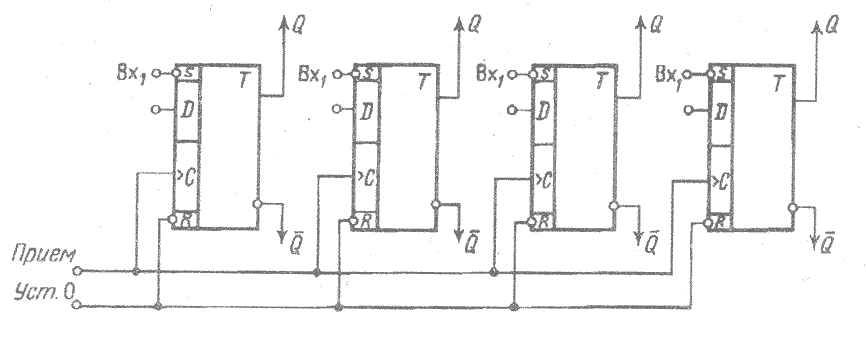
Рис. 3.5 Схема регистра

При передаче информации между двумя регистрами с помощью вспомогательных цепей можно обеспечить выполнение поразрядных операций: логического сложения ; логического умножения ; сложения по модулю два .

Здесь a_i и b_i — содержимое триггеров i-х разрядов регистров.

Регистры, выполняющие операцию сдвига, называются сдвигающими регистрами.

По способу межразрядных связей различают сдвигающие регистры

• с однопроводной передачей информации;

• с парафазной передачей информации.

По направлению сдвига рассматривают три типа регистров:

• сдвигающие вправо;

• сдвигающие влево;

• реверсивные сдвигающие регистры, которые в зависимости от управляющих сигналов осуществляют сдвиг кодов или вправо, или влево.

Если существуют цепи связей между младшим и старшим разрядами, то сдвигающие регистры называются кольцевыми. Такие схемы удобны для исследования, обладают свойствами деления частоты входных сигналов и могут быть использованы в качестве счетчиков.

На рисунке 3.6 представлена однофазная схема сдвигающего регистра на D-триггерах, реализующая сдвиг кодов вправо (D_i=Q_{i – 1}).

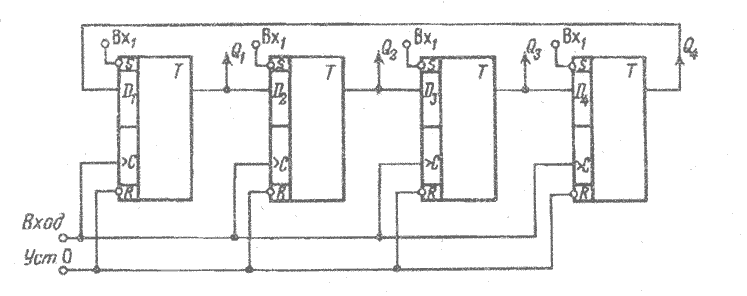
Рис. 3.6 Сдвигающий регистр на D-триггерах

Шина «Уст. 0», на которую подается сигнал установки нулевого слова, связана со входами R всех триггеров регистра.

Рассмотрим работу схемы в кольцевом режиме (выход триггера старшего разряда регистра связан со входом триггера младшего разряда) при наличии в регистре кода 1000. С приходом сигнала сдвига на входы синхронизации С всех D-триггеров происходит перезапись информации из каждого i-го разряда в (i+1)-й разряд и из 4-го в 1-й (за счет кольцевой связи). После поступления первого сигнала сдвига содержимое регистра представляет код 0100, после второго сигнала сдвига — 0010 и т.д. После поступления четырех сигналов сдвига восстанавливается начальное содержимое регистра 1000.

На рис. 3.7 представлена парафазная схема сдвигающего регистра, выполненная на J – K-триггерах и реализующая сдвиг вправо ( , ). Межразрядная связь осуществляется соединением выходов и триггера (i-1)-го разряда со входами j и k соответственно триггера i–го разряда. В этом включении J – K-триггер выполняет функцию D-триггера и работа сдвигающего регистра на J – K-триггерах аналогична работе сдвигающего регистра на D-триггерах.

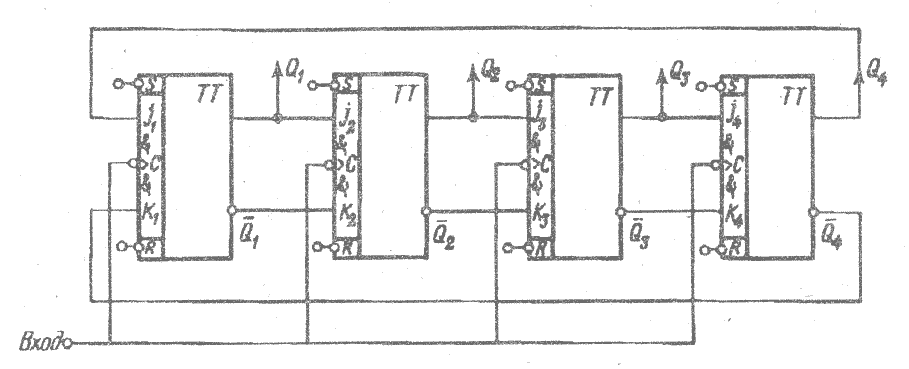
Рис. 3.7 Сдвигающий регистр на J – K-триггерах

Пример. Рассмотрим метод построения сдвигающих регистров на примере синтеза реверсивного регистра (при х=0 сдвиг на одни разряд вправо, при х=1 сдвиг на один разряд влево) на D- и J – K-триггерах.

Поскольку структура сдвигающего регистра регулярна, функции возбуждения определяются только для одного разряда.

Таблица перехода i–го разряда регистра представлена в столбцах 2..6 табл. 3.17 (при х=0 выход триггера Q_i(t+1)=Q_i+1(t), a при x=1 — Q_i(t+1)=Q_i-1(t)).

Таблица 3.17

№ п/п	Вход сигна-ла х	Время t			Время t+1	Функции возбуждения входов
1	2	3	4	5	6	7	8	9
1	0	0	0	0	0	0	0	b
2	0	0	0	1	0	0	0	b
3	0	0	1	0	0	0	b	1
4	0	0	1	1	0	0	b	1
5	0	1	0	0	1	1	1	b
6	0	1	0	1	1	1	1	b
7	0	1	1	0	1	1	b	0
8	0	1	1	1	1	1	b	0
9	1	0	0	0	0	0	0	b
10	1	0	0	1	1	1	1	b
11	1	0	1	0	0	0	b	1
12	1	0	1	1	1	1	b	0
13	1	1	0	0	0	0	0	b
14	1	1	0	1	1	1	1	b
15	1	1	1	0	0	0	b	1
16	1	1	1	1	1	1	b	1

По таблице переходов, используя матрицу переходов D- и J – K-триггеров, составляют функции возбуждения i–го разряда регистра столбцы (7…9 в табл. 3.17). Карты Вейча, представленные на рис. 3.8, позволяют получить минимальные формы функции.

Так, при использовании D-триггера имеем

.

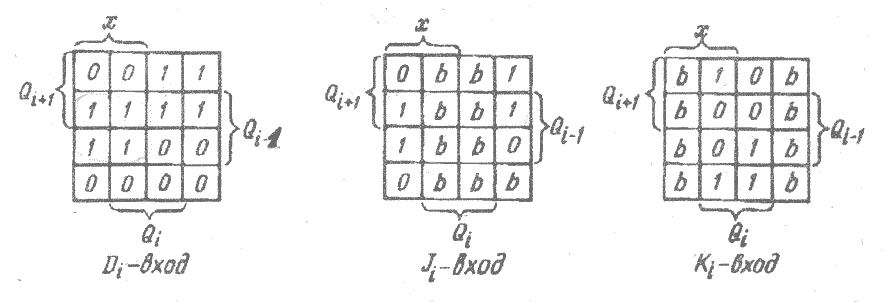
Рис. 3.8 Карты Вейча для реверсивного сдвигающего регистра

Если применяется J – K-триггер, то при значениях неопределенных коэффициентов b₁= b₂= b₇= b₈= b₉= b₁₂= b₁₃= b₁₀=1 и b₁= b₂= b₇= b₈= b₉= b₁₂= b₁₃= b₁₀=0 получим

; .

Из карт Вейча для функций J_i и K_i легко определить, что . Это упрощает структуру межразрядных связей регистра. По полученным функциям можно построить схему четырехразрядного реверсивного сдвигающего регистра, реализуемую на D-триггерах, для которой справедливы следующие соотношения:

в базисе И, ИЛИ, НЕ

; ;

; ,

в базисе И — ИЛИ — НЕ

; ;

; .

Схема реверсивного сдвигающего регистра на D-триггерах приведена на рис. 3.9, где каждый i-й разряд схемы соединен с (i-1)-м разрядом и (i+1)-м разрядом посредством логических схем 2И—2И—ИЛИ—НЕ. При сигнале «0» на шине управления реверсом (вправо/влево) под воздействием сигнала «сдвиг» осуществляется сдвиг информации вправо. В случае если на регистре был записан код 1000, то с приходом первого сдвигающего сигнала происходит перепись единичного сигнала по инверсному выходу из (i-1)-го разряда через схему 2И—2И—ИЛИ—НЕ в i-й разряд, при этом на (i-1)-м и (i+1)-м разрядах устанавливается нулевой сигнал, так как в (i+1)-м и в i-м разрядах в предыдущий момент времени был нулевой сигнал. В следующие такты работы регистра будет происходить сдвиг сигнала через схемы 2И—2И—ИЛИ—НЕ в (i+1)-й разряд, в (i+2)-й разряд, а далее за счет циклического переноса в (i+1)-й разряд.

При сигнале «1» на шине управления реверсом (вправо/влево) под воздействием сигнала «сдвиг» информация передвигается влево из (i+2)-го в (i+1)-й и из (i+1)-го в i-й разряд, а далее в (i-1)-й разряд.

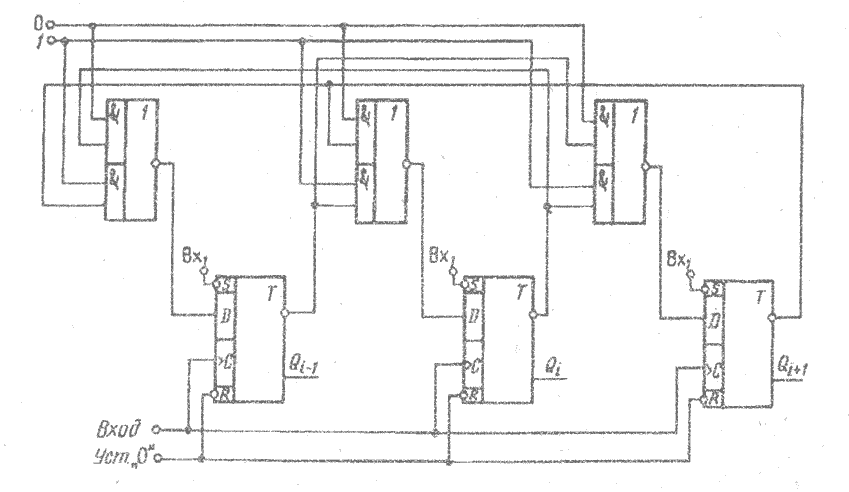
Рис. 3.9 Реверсивный сдвигающий регистр

Кольцевые сдвигающие регистры могут использоваться при построении счетчиков с постоянно взвешенными кодами, для которых число единиц и нулей в каждом устойчивом состоянии постоянно.

Счетчики. Счетчиком называется операционное устройство, фиксирующее число сигналов во входной последовательности.

По целевому назначению счетчики подразделяются на простые и реверсивные. Простые счетчики работают либо в режиме сложения (суммирующие счетчики), либо в режиме вычитания (вычитающие счетчики). Реверсивные счетчики реализуют оба режима счета. Операция счета представлена в таблице переходов (3.18).

Таблица 3.18

Сложение					Вычитание
Si(a)	φi-1(a)	Si+1(a)	φi(a)		Si(a)	ψ i-1(a)	Si-1(a)	ψ i(a)
0	0	0	0		0	0	0	0
0	1	1	0		0	1	1	1
1	0	1	0		1	0	1	0
1	1	0	1		1	1	0	0

Если соединение разрядов счетчика передает перенос (φ_i(a)) в старший разряд при переходе младшего разряда из состояния S_i(a) в состояние S_i+1(a)=0, то счетчик работает в режиме сложения:

;

.

Если перенос (заем) ψ _i(a) в старший разряд образуется при переходе младшего разряда из состояния S_i(a)=0 в состояние S_i-1(a)=0, то счетчик работает в режиме вычитания:

Основой построения счетчиков служат триггеры. Быстродействие счетчика зависит от реализации межразрядных соединений. Существует несколько способов передачи переносов: последовательный, параллельный, сквозной, групповой и др. Групповой перенос представляет комбинацию параллельного переноса в группе и сквозного между группами разрядов счетчика и наоборот.

В счетчике с последовательным переносом счетные сигналы подаются только на вход триггера первого разряда. Для каждого из последующих разрядов сигналы переноса поступают с выхода предшествующих разрядов. В результате происходит последовательное переключение разрядов счетчика. Быстродействие такого счетчика определяется задержкой распространения сигнала:

где n— количество разрядов в счетчике; t_dтр— средняя задержка триггера.

На рис. 3.10 а, б приведены схемы суммирующего, а на рис. 3.10 в, г — вычитающего счетчиков с последовательным переносом, собранных на J – K- и D-триггерах соответственно ( , — сложение, и — вычитание).

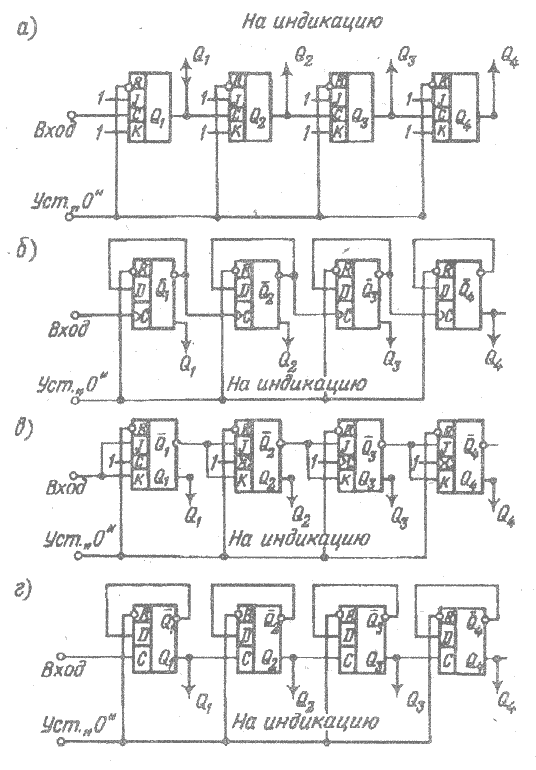
Рис. 3.10 Счетчик с последовательным переносом:

а, б — суммирующий; в, г — вычитающий

В счетчиках с параллельным переносом на информационный вход каждого разряда поступают сигналы с выходов всех предшествующих разрядов, а входной счетный сигнал одновременно (параллельно) поступает на синхровходы С триггеров всех разрядов. Счетчики с параллельным переносом обычно строятся на базе J – K- и D – V-триггеров, синхронизируемых фронтом сигнала. Быстродействие счетчика с параллельным переносом определяется задержкой сигнала на одном триггере: .

На рис. 3.11 представлены схемы суммирующего (вычитающего) счетчика с параллельным переносом на J – K-триггерах:

— суммирующий;

— вычитающий.

Алгоритм синтеза счетчиков рассмотрим на примере построения трехразрядного реверсивного синхронного счетчика (при х=0 суммирующий счетчик, при х=1 вычитающий счетчик) на J – K-триггерах.

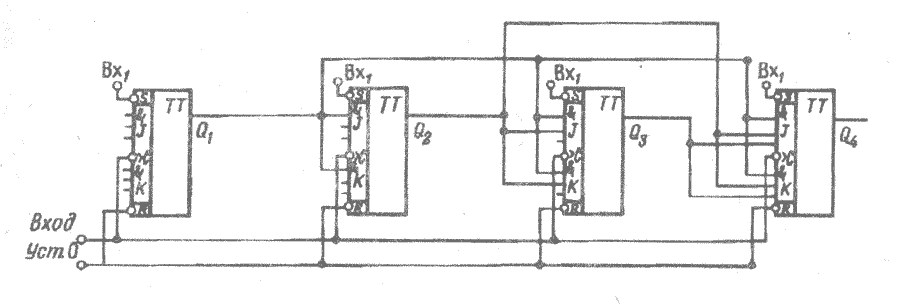
Рис. 3.11 Счетчик с параллельным переносом

Таблица переходов счетчика представлена в столбцах 2…8 (табл.3.19).

Таблица 3.19

№ п/п	Входной сигнал х	Время t			Время t+1			Функции возбуждения
		Q3	Q2	Q1	Q3	Q2	Q1	J3	K3	J2	K2	J1	K1
1	0	0	0	0	0	0	1	0	b	0	b	1	b
2	0	0	0	1	0	1	0	0	b	1	b	b	1
3	0	0	1	0	0	1	1	0	b	b	0	1	b
4	0	0	1	1	1	0	0	1	b	b	1	b	1
5	0	1	0	0	1	0	1	b	0	0	b	1	b
6	0	1	0	1	1	1	0	b	0	1	b	b	1
7	0	1	1	0	1	1	1	b	0	b	0	1	b
8	0	1	1	1	0	0	0	b	1	b	1	b	1
9	1	0	0	0	1	1	1	1	b	1	b	1	b
10	1	1	1	1	1	1	0	b	0	b	0	b	1
11	1	1	1	0	1	0	1	b	0	0	1	1	b
12	1	1	0	1	1	0	0	b	0	0	b	b	1
13	1	1	0	0	0	1	1	b	1	1	b	1	b
14	1	0	1	1	0	1	0	0	b	b	0	b	1
15	1	0	1	0	0	0	1	0	b	0	1	1	b
16	1	0	0	1	0	0	0	0	b	0	b	b	1

По табл. 3.19, с использованием матрицы переходов триггера, составляется функция возбуждения кодов счетчика (столбцы 9…14). Карты Вейча (рис. 3.12) позволяют получить минимальные формы функций:

;

;

,

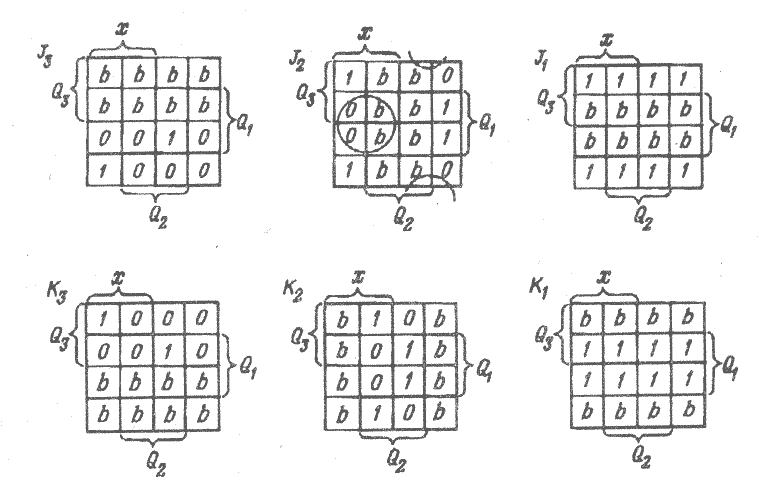
Рис. 3. 12 Карты Вейча для минимизации функций

по аналогии

;

.

Схема синхронного реверсивного счетчика с параллельным переносом, построенная на J – K-триггерах и элементах И — ИЛИ — НЕ, показана на рис. 3.13

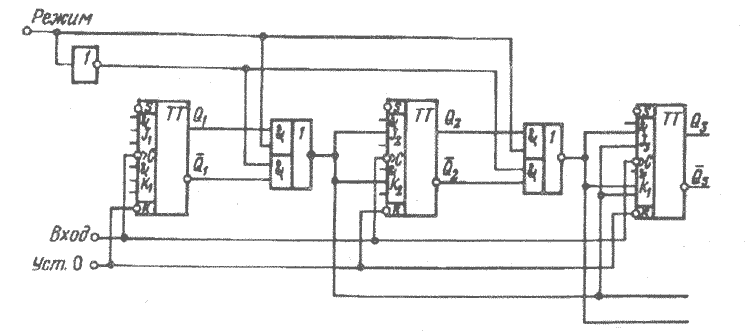Рис. 3.13 Синхронный реверсивный счетчик

В зависимости от управляющего сигнала х (сложение—вычитание) открывается схема И—НЕ межразрядных переносов либо для режима сложения, лило для режима вычитания.

Емкостью счетчика называется число его различных состояний. Двоичный n–разрядный счетчик на базе счетных триггеров имеет максимальную емкость С=2 ⁿ. Если входной сигнал снимается только со старшего разряда счетчика, то он указывает, что на выход подано 2 ⁿ сигналов.

Схема счетчика, фиксирующая выходной сигнал после поступления на его вход фиксированного числа сигналов, называется пересчетной схемой. Число входных сигналов, определяющих появление выходного сигнала, называется коэффициентом пересчета схемы. При наличии обратных связей n-разрядный двоичный счетчик имеет емкость К<2 ⁿ; такие схемы называются счетчиками по модулю К. Для построения асинхронной пересчетной схемы с заданным числом состояний К определяется:

количество разрядов n из условия

;

число неиспользованных состояний m

;

обобщенная функция сброса

,

которая подается на общую шину установки всего счетчика в нуль.

Пример. Рассмотрим построение декадного счетчика на J – K-триггерах и логической схеме И—НЕ. Декадный счетчик (к=10) можно получить из последовательного четырех разрядного счетчика с к=16, если при поступлении десятого сигнала, когда установится состояние выходов Q₄Q₃Q₂Q₁=1010, подать на общий вход установки нуля сигнал R = 1. Для этого используется управляющая комбинационная схема, выходная функция которой R равна 1 только при Q₄=Q₂=1 и при Q₃=Q₁=0. После минимизации функции сброса с использованием карт Вейча (рис. 3.14 а) получаем выражение функции , которая реализуется на двухвходовом элементе И—НЕ, подключаемом ко входу R последовательного счетчика. Схема декадного счетчика приведена на рис. 3.14 б.

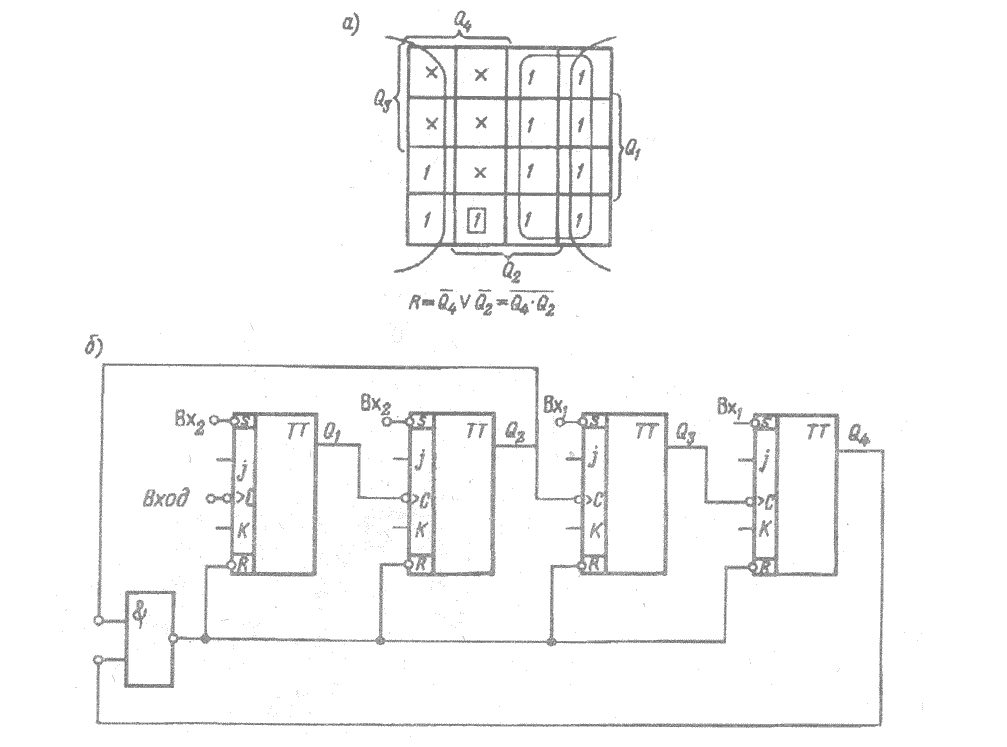
Рис. 3.14 Декадный счетчик: а — карта Вейча; б — схема декадного счетчика

При построении синхронных пересчетных схем используют методы структурного синтеза автоматов. Рассмотрим вышеприведенный пример. Кодированная таблица функций перехода и возбуждений декадного счетчика приведена в табл. 3.20.

Таблица 3.20

№ п/п	Время t				Время t+1				Функции возбуждения
	Q4	Q3	Q2	Q1	Q4	Q3	Q2	Q1	J4	K4	J3	K3	J2	K2	J1	K1
1	0	0	0	0	0	0	0	1	0	b	0	b	0	b	1	b
2	0	0	0	1	0	0	1	0	0	b	0	b	1	b	b	1
3	0	0	1	0	0	0	1	1	0	b	0	b	b	0	1	b
4	0	0	1	1	0	1	0	0	0	b	1	b	b	1	b	1
5	0	1	0	0	0	1	0	1	0	b	b	0	0	b	1	b
6	0	1	0	1	0	1	1	0	0	b	b	0	1	b	b	1
7	0	1	1	0	0	1	1	1	0	b	b	0	b	0	1	b
8	0	1	1	1	1	0	0	0	1	b	b	1	b	1	b	1
9	1	0	0	0	1	0	0	1	b	0	0	b	0	b	1	b
10	1	0	0	1	0	0	0	0	b	1	0	b	0	b	b	1

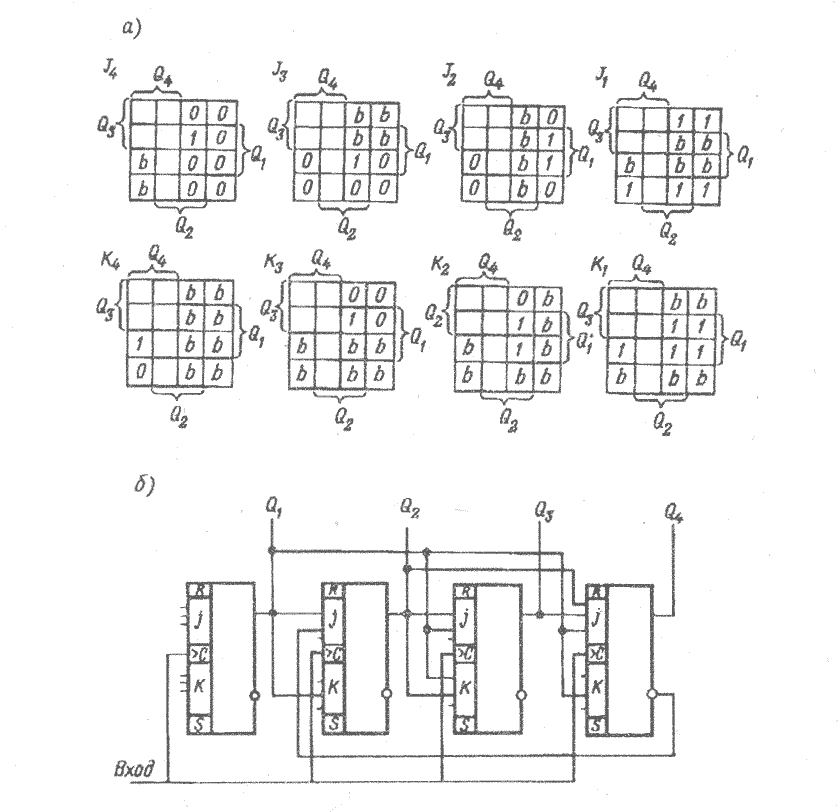
Рис. 3. 15 Декадный синхронный счетчик:

а — карты Вейча; б — схема декадного счетчика

Карты Вейча для минимизации функций представлены на рис. 3.15 а, из которых получаем выражения для функций возбуждения:

;

; ;

;

; .

Функциональная схема декадного синхронного счетчика приведена на рис. 3.15, б.

Сумматоры и вычитатели. Сумматором называется операционное устройство, выполняющее арифметическое (без учета знаков) сложение кодов чисел.

В зависимости от количества разрядов слагаемых, участвующих в сложении, различают одно- и многоразрядные сумматоры.

При сложении двух чисел независимо от системы счисления в каждом разряде суммируются три цифры две цифры данного разряда слагаемых и цифра переноса из соседнего младшего разряда. В результате сложения определяются две цифры: цифра данного разряда суммы и цифра переноса в следующий разряд.

Одноразрядный полный сумматор представляет собой схему, имеющую три входа и два выхода, работа которой описывается булевыми функциями согласно таблице истинности (табл. 3.21) полного сумматора:

сумма:

;

перенос:

,

где a_ib_i — цифра i–го разряда слагаемых; C_i-1 — перенос из предыдущего младшего разряда; S_i — цифра i–го разряда суммы; C_i — перенос в следующий старший разряд.

Таблица 3.21

ai	bi	Ci-1	Si	Ci	ai	bi	Ci-1	Si	Ci
0	0	0	0	0	1	0	0	1	0
0	0	1	1	0	1	0	1	0	1
0	1	0	1	0	1	1	0	0	1
0	1	1	0	1	1	1	1	1	1

Рис. 3.16 Одноразрядный комбинационный сумматор

Указанные функции (или логически эквивалентные им) реализуются за одни или несколько тактов работы схемы, что позволяет получать различные виды двоичных сумматоров.

Комбинационный сумматор не обладает свойством памяти, коды слагаемых поступают на входы сумматора одновременно, выходные сигналы вырабатываются только во время действия входных сигналов.

На рис. 3.16 представлены схемы одноразрядного комбинационного сумматора, реализованного на разных типах элементов, выходные функции которого имеют вид:

элементы И — ИЛИ — НЕ:

;

,

элементы И— НЕ:

;

.

Выходные сигналы схемы вырабатываются непосредственно после одновременной подачи входных сигналов, т.е. работа схемы однотактная. При снятии сигналов со входов схемы выходные сигналы теряются.

Быстродействие одноразрядного комбинационного сумматора характеризуется временем установления выходных сигналов суммы и переноса после подачи входных сигналов. Наиболее важным с точки зрения быстродействия является время формирования сигнала переноса, так как при образовании многоразрядного сумматора из одноразрядных схем сигнал переноса может распространяться от разряда к разряду. Для увеличения быстродействия сумматоров используется принцип одновременного (параллельного) переноса, когда входной перенос каждого разряда вырабатывается независимо от переноса соседнего младшего разряда.

Перепишем уравнение i–го разряда сумматора в несколько ином виде. Если в уравнении входного сигнала переноса i–го разряда множитель C_i вынести за скобки, получим . Введем два дополнительных уравнения и , здесь P_i и σ_i представляют собой сигналы передачи и генерирования переноса. Тогда уравнение для переноса можно записать в виде

,

а уравнение суммы —

.

Уравнения суммы и выходного сигнала переноса четырехразрядного сумматора с одновременным переносом имеют вид:

;

;

;

;

.

Недостатком сумматора с одновременным переносом является то, что при увеличении его разрядности функции переноса становятся все более сложными; в конечном счете практически нереализуемыми из-за большого числа внутренних соединений и перегрузки схем, генерирующих функции P_i и σ_i.

Для построения многоразрядного параллельного комбинационного сумматора его проектируют как устройство, состоящее из нескольких секций, для которых вводят вспомогательные функции σ и P:

;

.

Необходимо отметить, что ни одно из этих уравнений не содержит входного сигнала переноса в секцию. В связи с этим функции σ и P не зависят от числа секций, образующий сумматор, и реализуются с минимальной задержкой.

С целью для каждой четырехразрядной секции входного сигнала переноса, который зависел бы от результатов выполнений операций в младших секциях, сигналы, соответствующие функциям σ и P, можно подать на входы схем элемента «И». В этом случае входной сигнал переноса в секцию описывается следующим уравнением:

.

Вычитателем называется операционное устройство, выполняющее арифметическое вычитание кодов чисел.

В зависимости от количества разрядов операндов, участвующих в операциях, различают одно- и многоразрядные вычитатели.

При вычитании двух чисел в каждом разряде вычитаются три цифры: две цифры данного разряда и цифра займа из соседнего старшего разряда. В результате вычитания определяются две цифры: цифра разности и цифра займа в следующий разряд.

Одноразрядный полный двоичный вычитатель представляет по аналогии с сумматором схему, имеющую три входа и два выхода, работа которой описывается булевыми функциями, согласно таблице истинности (табл. 3.22).

Таблица 3.22

ai	bi	Зi+1	Si	Зi	ai	bi	Зi+1	Si	Зi
0	0	0	0	0	1	0	0	1	0
0	0	1	1	1	1	0	1	0	0
0	1	0	1	1	1	1	0	0	0
0	1	1	0	1	1	1	1	1	1

Разность

;

заем

.

По аналогии с полным сумматором полный вычитатель можно собрать на элементах И — ИЛИ — НЕ и И — НЕ (заменив в операции заем на ) (рис.3.17):

на элементах И — ИЛИ — НЕ

;

,

на элементах И — НЕ

;

.

Четырехразрядный комбинационный вычитатель с одновременным переносом

;

.

Вводя две дополнительные функции и , получим

;

;

;

;

.

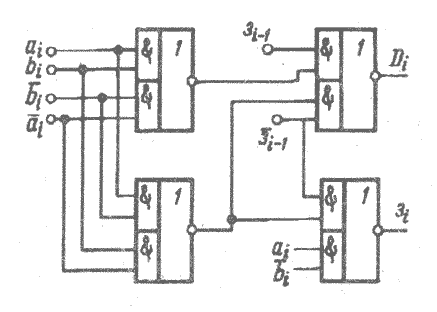
Рис. 3. 17 Одноразрядный комбинационный вычитатель

Необходимо подчеркнуть, что все эти уравнения могут быть записаны в виде выражений, в которые входят только значения входных сигналов a_i, b_i, З₀ четырехразрядного вычитателя.

Распределители сигналов. Распределителем сигналов называется устройство, которое при поступлении на его вход переключающих сигналов формирует управляющий сигнал в одном из выходных каналов.

В зависимости от назначения распределители различаются числом переключающих входов, каналов, а также длительностью частотой и порядком следования формируемых сигналов.

По виду формируемых сигналов распределители сигналов классифицируются следующим образом:

распределители сигналов (потенциалов);

распределители импульсов;

комбинированные распределители.

Распределители сигналов (потенциалов) формируют выходной сигнал во время подачи переключающего сигнала и сохраняют его до прихода следующего переключающего сигнала; длительность выходного сигнала определяется периодом следования переключающих сигналов. Распределители сигналов служат основой для построения импульсных и комбинированных распределителей.

В распределителях импульсов выходной сигнал формируется только во время совпадения переключающего и стробирующего входного сигналов; длительность выходного сигнала определяется длительностью стробирующего импульса.

Распределители комбинированного типа имеют как потенциальные, так и импульсные выходы.

Схема распределителя сигналов (рис. 3.18) содержит устройство формирования параллельного кода и дешифратор. В качестве устройства формирования кода используются кольцевые сдвигающие регистры с прямыми и перекрестными связями и двоичные счетчики.

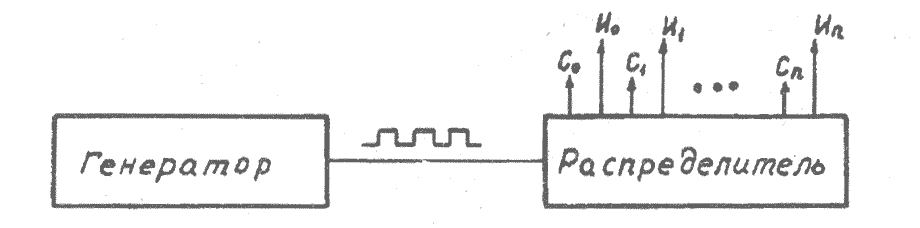
Рис. 3. 18

Распределители сигналов на счетчиках. При построении схем распределителей наиболее удобны счетчики с параллельным переносом, обладающие высоким быстродействием и не вызывающие ложного включения каналов при переходе из одного состояния в другое.

На рис. 3.19а приводится схема 8-канального однотактного распределителя сигналов, использующая трехразрядный счетчик на триггерах J – K и полный линейный дешифратор на элементах И — НЕ (управляющий сигнал в каналах представлен логическим нулем). Длительность управляющего сигнала равна периоду следования переключающих сигналов, поступающих с выхода счетчика (рис. 3.19б).

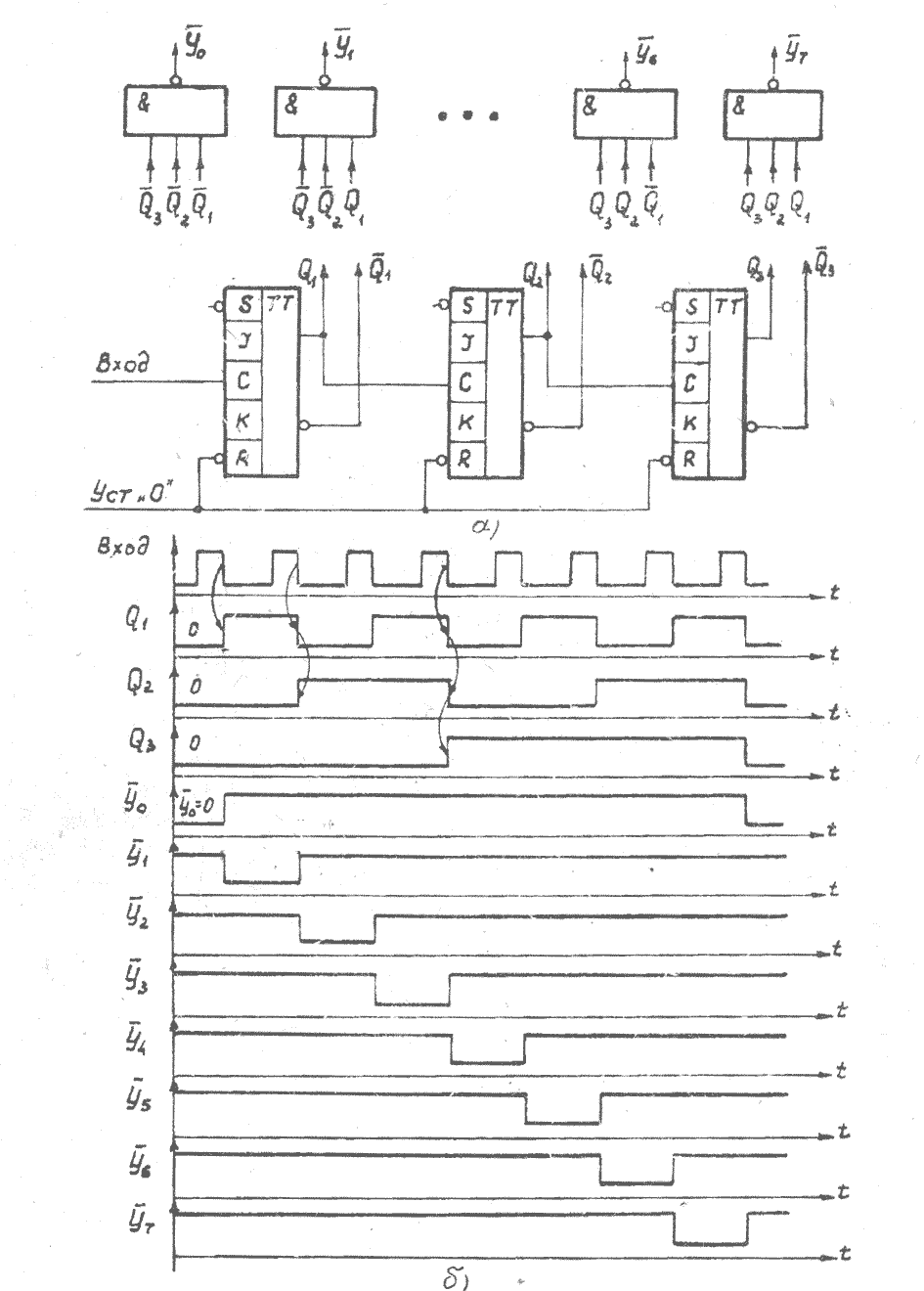
Рис. 3.19

Работа схемы поясняется таблицей состояний и выходов распределителя сигналов (табл. 3.23).

Таблица 3.23

Состояние счетчика			Выход каналов уi
			0
			1
			2
			3
			4
			5
			6
			7

Из таблицы состояний для каждого выхода распределителя справедливы следующие соотношения:

; ; ; ; ; ; ; .

Для реализации распределителя импульсов на выходные схемы И — НЕ дешифратора следует подать через дополнительный вход стробирующий импульс, который и будет определять длительность выходного сигнала.

Распределители на регистрах. К достоинствам этих схем распределителей относятся высокое быстродействие, простота схем дешифрации, регулярность топологии разрядов; к недостаткам — наличие запрещенных состояний.

Рассмотрим методику синтеза распределителей на примере построения схемы трехканального распределителя сигналов, выдающей в следующем порядке выходные сигналы: 1, 1, 3, 3, 2, 1 и реализованной на базе регистра — счетчика Джонсона. Так как длина последовательности номеров каналов равна 6, то выбираем трехразрядный счетчик Джонсона. Занесем условия примера в таблицу состояний и выходов (табл. 3.24).

Таблица 3.24

Состояние счетчика Джонсона			Выход каналов уi
			уi
0	0	0	1
1	0	0	1
1	1	0	3
1	1	1	3
0	1	1	2
0	0	1	1

Из табл. 3.24 определяем для выходной последовательности сигналов:

;

;

.

Минимизируя выражения с учетом запрещенных комбинаций и , получаем:

; ; .

В базисе И — НЕ

; ; .

Из последнего выражения видно, что для реализации у₁ нужно использовать одноступенчатую логику И — НЕ, а для реализации у₂ и у₃ — двухступенчатую логику, поэтому для выравнивания логики запишем:

.

На рис. 3.20 представлена схема трехканального распределителя сигналов на счетчике Джонсона, реализованном на триггерах типа D с инверсной связью выхода Q₁ со входом D₃, формирующая заданную последовательность кодов.

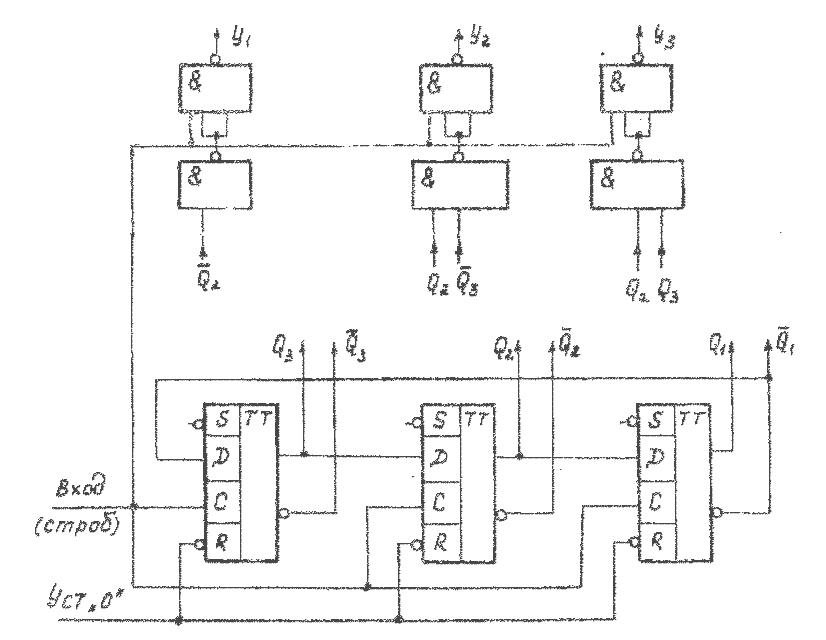
Рис. 3. 20

В общем случае как число каналов распределителя, так и последовательность их включения могут быть заданы достаточно произвольно. При этом определяющей величиной для построения схемы распределителя является не число каналов, а длина повторяющейся последовательности номеров включаемых каналов. Эта величина соответствует числу различных состояний схемы формирования кодов, и если она кратна степени 2, то в распределителе используется полный дешифратор. В противном случае применяется неполный дешифратор, функции которого минимизируются с учетом запрещенных состояний схемы формирования кодов.

Выходы дешифратора с помощью логических схем объединяются согласно повторению номеров на выделенном участке.