Берем двойное отрицание от каждой суммы

Рассмотрим элементарную сумму

Q_i= a_i +b_i …+l_i,

где a_i = x₁ или ; b_i = x₂ или и т.д.

Отсюда f(x₁ x₂… x_n)=

Таким образом, чтобы перейти от КНФ к функции Пирса, следует заключить в скобки все элементарные суммы, затем все знаки дизъюнкции и конъюнкции заменить знаком стрелка Пирса и выразить инверсные переменные через операцию стрелка Пирса:

или .

При этом следует помнить, что каждая элементарная сумма исходного выражения должна иметь не менее двух переменных, что можно получить с помощью соотношения

A=A+0 или A=A+A.

Пример.

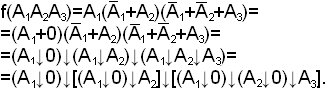
3. После получения записи исходной функции в базисе {↓} перед построением структурной схемы следует рассмотреть возможность упрощения схемы за счет группировки скобочных выражений по следующим правилам:

а) Если несколько выражений, заключенных в скобках, содержат в общих для них переменных по одной переменной с инверсией, то эти инверсные переменные можно образовать на одном элементе.

Пример.

[A↓(B↓0) ↓C] ↓ [A↓B↓(C↓0)]=[A↓C↓(B↓C)] ↓ [A↓B↓(B↓C)].

б) Если несколько выражений, заключенных в скобки, содержат по одной инверсной переменной не в общих для них переменных, то эти инверсные переменные можно организовать на одном элементе.

Пример.

[A↓B↓(C↓0)] ↓ [A↓B↓(D↓0)]= ↓[A↓B↓(C↓D)] ↓ 0.

Справедливость записей правил группировки можно проверить преобразованиями в системе { ↓ }. При этом оба правила могут быть применены и одновременно.

4. Последним этапом синтеза является составление структурной схемы на элементах «ИЛИ-НЕ».

Пример. Составить структурную схему на элементах «ИЛИ-НЕ», реализующую функцию

1. Проводим преобразования исходя из ДНФ заданной функции:

а) построим схему по заданной ДНФ:

б) построим схему исходя из МДНФ заданной функции:

.

Используя второе правило группировки, получаем

Для данной функции минимизации ДНФ позволила значительно упростить схему, однако это справедливо не для всех функций (рис. 2,а).

2. Чтобы определить минимальную структурную схему, проведем аналогичные преобразования в КНФ

в МКНФ

Т

A

аким образом, МКНФ (ABC) позволила получить минимальную структурную схему (рис. 2,б).

Синтез схем на элементах типа «И-НЕ» (А|B).

1. Функция задана в ДНФ

К аждое элементарное произведение

Отсюда имеем

f(x₁ x₂… x_n)=( x₁ |x₂ |…| x_k )|(x₁ |x₂|…| x_n )|…|(x₁ |x₂|…|x_l ).

Таким образом, чтобы от ДНФ перейти к базису { | }, надо заключить в скобки все элементарные произведения, заменить все знаки дизъюнкции и конъюнкции на знак операции Шеффера и записать инверсные переменные через операции Шеффера, пользуясь соотношением или

При этом необходимо, чтобы каждый дизъюнктивный член содержал не менее двух переменных, для чего следует воспользоваться соотношением

.

Пример.

2. Функция задана в КНФ

Каждая элементарная сумма

Таким образом, имеем

Для того чтобы переключательную функцию, записанную в КНФ, выразить в базисе {|}, необходимо заключить в скобки все конъюнктивные члены, заменить все знаки конъюнкции на знак операции Шеффера, взяв инверсию от каждой переменной и от выражения в целом. И выразить все инверсии через операцию Шеффера, пользуясь соотношениями или

При этом необходимо, чтобы каждая элементарная сумма содержала не менее двух переменных, для чего можно воспользоваться соотношением

А=А+0.

Пример.

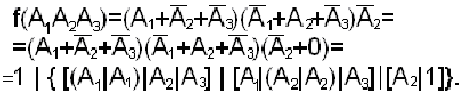
3. После получения записи исходной функции в базисе {|} перед построением структурной схемы следует рассмотреть возможность упрощения схемы за счет группировки скобочных выражений по следующим правилам.

1. Если несколько выражений, заключенных в скобках, содержат в общих для них переменных по одной переменной с инверсией, то эти инверсные переменные можно образовать на одном элементе.

Пример.

f(ABC)=1 | [A|(B|B)|C] | [A|B|(C|C)]=1 | [A|C|(B|C)] | [A|B|(B|C)].

а) Если несколько выражений, заключенных в скобках, содержат по одной инверсной переменной не в общих для них переменных, то эти инверсные переменные можно образовать на одном элементе.

Пример.

f’(ABCD)=1 | {[A|B|(C|C)] | [A|B|(D|D)]}=1 | {A|B|(C|D)}.

4.Последним этапом синтеза является составление структурной схемы на элементах «И-НЕ».

Пример. Построить схему на элементах «И-НЕ», реализующую функцию

1. Используем заданную ДНФ функции (она является минимальной)

2. Воспользуемся МКНФ исходной функции

имеет две МКНФ;

Перейдем к базису {|}:

Все формы дали одинаково сложные структурные схемы.

Пример. Составить структурную схему на элементах типа «ИЛИ-НЕ», реализующую функцию

f(ABCD)=m₀+ m₂+ m₄+ m₅+ m₆+ m₇+ m₁₀+ m₁₁+ m₁₃+ m₁₄+ m₁₅.

1. МДНФ исходной функции определим с помощью карты Вейча:

2. Сокращенную конъюнктивную нормальную форму исходной функции определяем также с помощью карты Вейча обратной функции.

Из карты обратной функции следует, что сокращенная

ДНФ:

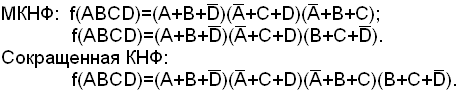
Группировка обязательных импликант и дает общий элемент (A↓D).

Минимальные конъюнктивные формы дадут еще элементы (D↓D) или (С↓С).

В сокращенной форме обе необязательные импликанты дадут общий элемент (А↓D):

Требуется 5 элементов типа «ИЛИ-НЕ».

Пример. Составить структурную схему на элементах типа «И-НЕ», реализующую функцию:

f(ABCD)=m₅+m₁₀+ m₁₂+ m₁₃+ m₁₄.

1. Находим простые импликанты функции, используя метод Квайна:

Таблица 22

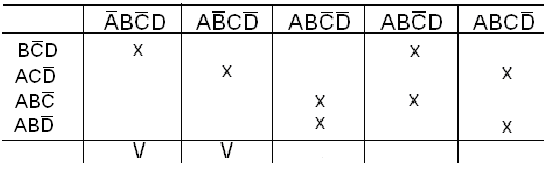
Из табл.33 следует, что и - обязательные импликанты функции.

Рассматриваем возможность группировки простых импликант с целью уменьшения числа элементов «И-НЕ» в структурной схеме.

1-я форма МДНФ.