Метод Блека-Порецкого.

Используется для получения сокращенной ДНФ из любой произвольной функции представления [5].

Идея построения сокращенной ДНФ по произвольной ДНФ вытекает из следующего определения: если в ДНФ для данной функции f(x₁ … x_n) входит две конъюнкции вида Ax_i и Bx_i, то имеет место равенство D=D\/AB, где D – ДНФ, эквивалентная функция f.

Алгоритм метода Блека-Порецкого.

1. Провести все возможные склеивания любых двух смежных термов, представляющих соответствующие элементарные конъюнкции, получить L-разрядный троичный набор и построить матрицу ранга n.

2. Над полученными элементарными конъюнкциями ранга (n-1) провести операции склеивания и поглощения, образовать элементарные конъюнкции нижнего ранга и т.д.

3. Процесс закончить, когда после операции склеивания и поглощения окажется, что в ДНФ отсутствуют члены, дальнейшее поглощение которых невозможно, т.е. когда будет получена сокращенная ДНФ.

4. Строится импликантная матрица и определяется максимальное покрытие.

Метод удобен при машинных способах минимизации.

Пример. Найти минимальную форму для заданной функции:

1. Матрица исходных данных 3. Матрица ранга (n-2)

0 0 0 1 2 0 2 1

0 0 1 0 2 0 2 1

0 0 1 1 2 0 1 2

1 0 0 1 2 0 1 2

1 0 1 0

1 0 1 1

2. Матрица ранга (n-1)*

0 0 2 1

2 0 0 1

0 0 1 2

2 0 1 0

2 0 1 1

1 0 2 1

1 0 1 2

4. Вычеркиваем одинаковые строки матрицы ранга (n-2) и получаем

A B C D

2 0 2 1

2 0 1 2

5.

где 0 – инверсия переменной, 1 – переменная, 2 – отсутствует переменная.

§6. Минимальные конъюнктивные нормальные формы булевых функций.

Существует несколько методов получения МНКФ функций, использующих понятие простой импликанты, понятия вхождения и накрытия функций, сокращенных и минимальных КНФ аналогично соответствующим понятиям для дизъюнктивных нормальных форм.

Рассмотрим наиболее простой алгоритм поиска МКНФ, использующий выражение МКНФ через инверсию от МКНФ обратной функции.

Обратной функцией f₁(x₁ x₂ … x_n) называется

f ₂(x₁ x₂ … x_n)= f₁(x₁ x₂ … x_n).

Алгоритм метода.

1. исходную функцию представляют в СДНФ;

2. находят СДНФ обратной функции;

3. пользуясь любым из известных методов, находят МДНФ обратной функции;

4. инверсия от МДНФ обратной функции после соответствующих преобразований с использованием формул де Моргана представляет МКНФ исходной функции.

Пример. Найти МКНФ функции:

1. СДНФ

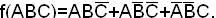
2. Так как обратная функция имеет значение 1 на тех наборах, на которых f(ABC) принимает значение 0, то в СДНФ обратной функции входят те минтермы, которые отсутствуют в СДНФ функции f(ABC):

СДНФ

3. Используем метод карт Вейча для отыскания МДНФ обратной функции (рис.9). Сокращенная ДНФ включает простые импликанты: A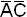C, , BC, .
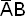