§4. Метод импликантных матриц.

Рассмотрим графический метод отыскания тупиковых форм функции из сокращенной ДНФ.

Импликантная матрица представляет собой таблицу, столбцы которой соответствуют всем конституентам единицы СДНФ заданной функции, а строки – всем простым импликантам.

В таблице по строке каждой импликанты отмечаются те минтермы, которые ею поглощаются.

Чтобы получить минимальную ДНФ заданной функции, достаточно найти минимальное число импликант, которые совместно накрывают все столбы импликантной матрицы, если в каком-либо из столбцов составленной импликантной матрицы функции имеется только одна отметка, то соответствующая ей импликанта является обязательной и обязательно входит в тупиковую форму функции, так как без нее будет получено накрытие всего множества минтермов.

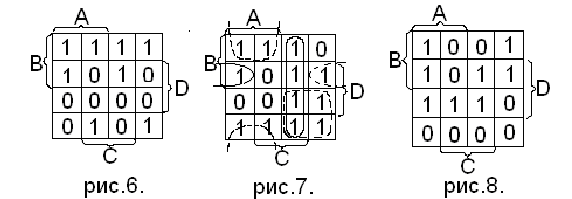
Для случая имеем импликантную матрицу, представленную в табл.18.

В данном случае импликанты AC и являются обязательными. Их сумма покрывает все минтермы, следовательно, тупиковая форма Она единственна и поэтому является минимальной.

Таблица 18.

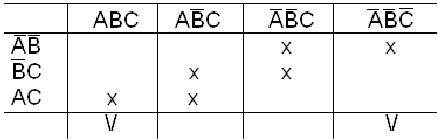
Пример. Найти минимальную ДНФ функции, используя метод Квайна и метод импликантных матриц:

Сокращенная ДНФ

Импликантная матрица функции дана в табл.19.

Таблица 19

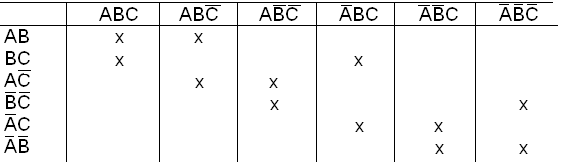
Так как нет столбцов с одной отметкой, то ни одна из импликант не является обязательной. Найдем минимальное количество простых импликант, накрывающее все колонки.

Возможны две тупиковые формы функции:

;

Обе формы содержат одинаковое число букв и, следовательно, обе являются минимальными.

Возможны другие тупиковые формы данной функции, но они не минимальны:

§5. Минимизация булевых функций с помощью карт Вейча.

Это наиболее удобный метод минимизации булевых функций при небольшом числе переменных.

Карта Вейча для двух переменных (а), для трех (б), для четырех (в), для пяти (г), представляет собой таблицу с определенным порядком следования наборов (в клетках таблицы – номера минтермов соответствующего числа переменных) (рис.3).

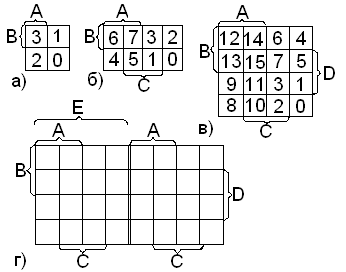
Рис.3.

Для удобства пользования картами на полях проставляют значения переменных.

Таблица функции записывается в карту обычным способом 1(0) – в квадратах, соответствующих наборам, где f(x₁ x₂ … x_n)=1(0).

Следует иметь виду, что порядок расположения наборов таков, что при переходе между соседними квадратами по строке или столбцу меняется форма лишь одной переменной в наборе. В этом смысле первая строка карты является соседней с последней, а первый столбец – соседний с последним.

Отсюда возникают возможности проведения операции склеивания, исходя из расположения единиц в карте Вейча.

Правила склеивания с помощью карт Вейча.

Два минтерма склеиваются (рис.4), если они расположены:

1. по соседству – в одной строке или одном столбце (рис.4,а);

2. в противоположных концах одной строки или одного столбца (рис.4,б);

3. в одинаковых местах двух карт (рис.4,в), последнее – для n>4.

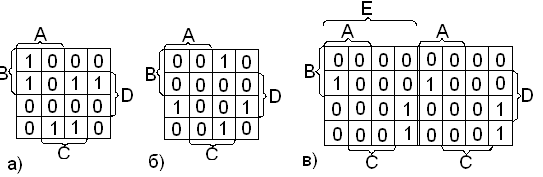
рис.4.

Алгоритм метода минимизации с помощью карт Вейча.

1. Нанести функцию на карту.

2. Каждый квадрат, содержащий «1», проанализировать с точки зрения «склеивания» с другими во всех возможных комбинациях.

3. Выбираются те комбинации, которые объединяют наибольшее количество единиц и при этом накрывают все единицы карты функции. Они являются простыми импликантами функции.

4. Если только одна импликанта покрывает какую-либо единицу на карте, то эта импликанта является существенной (обязательной).

5. Из совокупности простых импликант выбираются минимальные формы функции.

Метод позволяет получить все возможные МДНФ: