МІНІСТЕРСТВО ОСВІТИ І НАУКИ, молоді та спорту україни

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ КОРАБЛЕБУДУВАННЯ

ІМЕНІ АДМІРАЛА МАКАРОВА

О.С. Манойленко, І.А. Зоріна,

Є.В. Сокуренко, В.П. Борко

МЕТОДИЧНІ ВКАЗІВКИ

ДЛЯ САМОСТІЙНОЇ та індивідуальної роботи

студентів, підсумково-модульного контролю

з вищої математики за темою

"ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ"

Миколаїв НУК 2013

МІНІСТЕРСТВО ОСВІТИ І НАУКИ,

молоді та спорту україни

Національний університет кораблебудування

імені адмірала Макарова

О.С. Манойленко, І.А. Зоріна,

Є.В. Сокуренко, В.П. Борко

МЕТОДИЧНІ ВКАЗІВКИ

для самостійної та індивідуальної роботи студентів,

підсумково-модульного контролю

з вищої математики за темою

"Функції багатьох змінних"

Рекомендовано Методичною радою Херсонської філії НУК

Електронне видання

комбінованого використання на DVD-ROM

Миколаїв НУК 2013

УДК 517(076)

ББК 22.11я73

М54

Укладачі: О.С. Манойленко, канд. техн. наук., доцент;

Є.В. Сокуренко, канд. техн. наук., доцент;

І.А. Зоріна, канд. фіз.-мат .наук., доцент;

В.П. Борко, канд. фіз.-мат. наук., доцент

Рецензент М.Б. Літвінова, канд. фіз.-мат. наук., доцент

Методичні вказівки для самостійної та індивідуальної роботи студентів, підсумково-модульного контролю з вищої математики за темою "Функції багатьох змінних"/ О.С. Манойленко, І.А. Зоріна, Є.В. Сокуренко, В.П. Борко. - Миколаїв: Видавництво НУК, 2013. – 67с.

Методичні вказівки відповідають програмі курсу вищої математики та призначені для надання допомоги студентам технічних та економічних спеціальнос­тей денної та заочної форми навчання при виконанні контрольних робіт, розрахунково-графічних завдань, підготовки до підсумково-модульного контролю, самостійної роботи. Містять теоретичні відомості з приклада­ми, задачі з докладними розв'язками, варіанти контрольних та розра­хунково-графічних завдань.

Призначено для студентів технічних спеціальностей ХФ НУК.

 Манойленко о.С., Зоріна і.А., Сокуренко є.В., Борко в.П., 2013

 Національний університет кораблебудування

імені адмірала Макарова, 2013

Тема 1

ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ

Основні поняття

1.1. Множини точок на площині та в n-вимірному просторі

Упорядкованій парі чисел на координатній площині відповідає одна точка . Аналогічно, в n-вимірному просторі n упорядкованим дійсним числам відповідає одна точка , де числа - координати цієї точки. З метою скорочення запису далі розглядатимемо множини точок на площині, але подані далі означення можна вважати правильними і в разі n-вимірного простору.

Означення. Множина точок називається зв’язною, якщо будь-які її дві точки можна сполучити ламаною лінією так, щоб усі точки цієї лінії належали цій множині.

Приклад. На рис.1 у випадку а) буде зв’язна множина, а у випадку б) — не зв’язна.

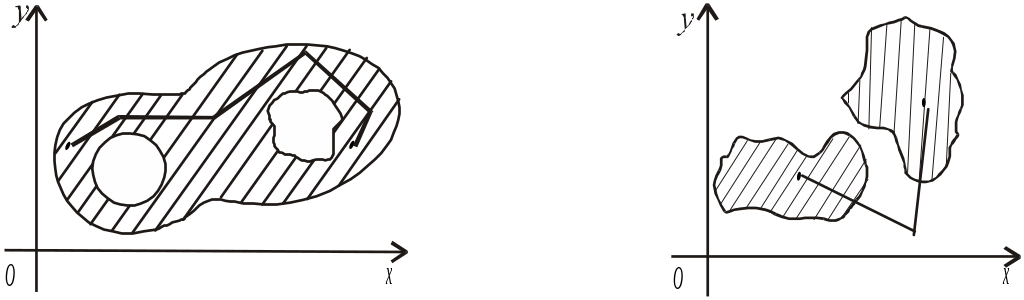
а) б)

Рис.1

Означення. Множина точок називається обмеженою, якщо всі її точки належать множині точок круга скінченного радіуса.

Приклад. На рис.2 у випадку а) маємо обмежену множину, а у випадку б) — необмежену.

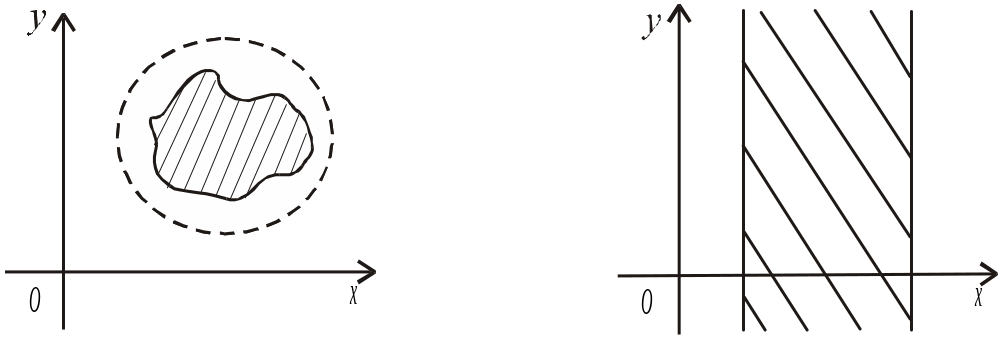
а) б)

Рис.2

Означення. Множина точок, координати яких задовольняють нерівність

(1)

називається -околом точки .

Зауваження. У випадку двовимірного простору нерівність (1) можна подати у вигляді

(2)

Вона визначає внутрішність круга з радіусом та з центром у точці (рис.3). Якщо з -околу точки вилучимо саму точку , дістанемо виколотий -окіл точки .

Рис.3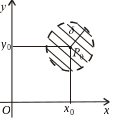

Означення. Точка називається внутріш­ньою для множини точок, якщо вона належить цій множині разом з деяким своїм -околом, і зовнішньою, якщо існує її окіл з точок, жодна з яких не належить цій множині.

Означення. Зв’язна обмежена множина, яка складається тільки з внутрішніх точок, називається відкритою областю (або просто областю).

Область позначатимемо:

.

У частинному випадку, коли D — прямокутник, область позначатимемо

.

Приклад. На рис.4 множина точок D — область:

.

Означення. Точка називається межовою для області, якщо в будь-якому її -околі існують точки, що не належать області та належать їй.

Означення. Множина межових точок називається межею області.

Означення. Область, об’єднана зі своєю межею, називається замкненою областю.

Приклад. На рис.5 — замкнена область, — рівняння межі області, К — внутрішня, L — зовнішня, М — межова точка.

Означення. Множина називається опуклою, якщо будь-які точки множини можна зв’язати відрізком, який буде належати цій множині.

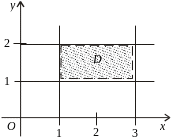
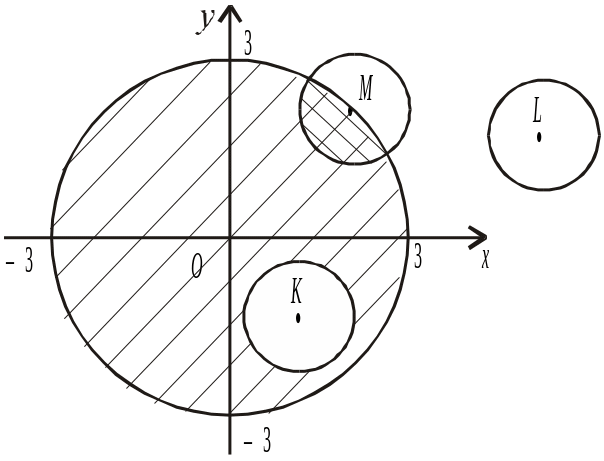
Рис. 4 Рис. 5

1.2. Означення функції багатьох змінних

Означення. Якщо кожній точці множини D n-вимірного простору поставлено у відповідність за деяким законом одне і тільки одне дійсне число , то кажуть, що в області задано функцію n незалежних змінних . При цьому D називають областю визначення функції, Е — областю значень функції.

Згідно з означенням функцію можна розглядати як функцію точки і записувати .

Зокрема, при n = 2 говорять, що задана функція двох змінних , якщо кожній парі на площині поставлено у відповідність тільки одне число z.