3 Этап. Моделирование зависимости между значениями, объективно влияющих факторов и численностью управленческого персонала по функции управления.

Содержание этого этапа заключается в разработке норматива численности персонала по каждой функции управления, через который косвенно отражается трудоемкость работ по функции управления, а значит и численность управленческого персонала.

Выбор математического метода для обработки данных.

При разработке норматива требуется найти нормативную формулу зависимости численности персонала от факторов, влияющих на нее, отражающей ее характер и позволяющей наиболее точно определить тенденцию изменения численности управленческого персонала в зависимости от изменения значений факторов и обеспечивающей минимальные отклонения фактической численности от расчетной - уравнение регрессии. Наиболее распространенными методами получения зависимости являются:

• графоаналитический метод для установления коэффициентов регрессии при однофакторной зависимости;

• метод множественной корреляции для установления параметров многофакторной зависимости.

Графоаналитический метод предполагает установление характера зависимости путем нанесения на график фактических значений фактора и соответствующей численности управленческого персонала на i-м предприятии и построения нормативной кривой так, чтобы среднеквадратическое отклонение фактических значений численности от нормативной кривой, измеренных по оси ординат, было минимальным. Критерием построения этой линии является функция:

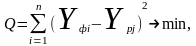
где Y_фi – фактическая численность персонала;

Y_рj – численность, согласно нормативной линии;

n – количество анализируемых базовых предприятий.

Моделирование зависимости Y=f(X) в данном случае представлено на рис. 8.1.

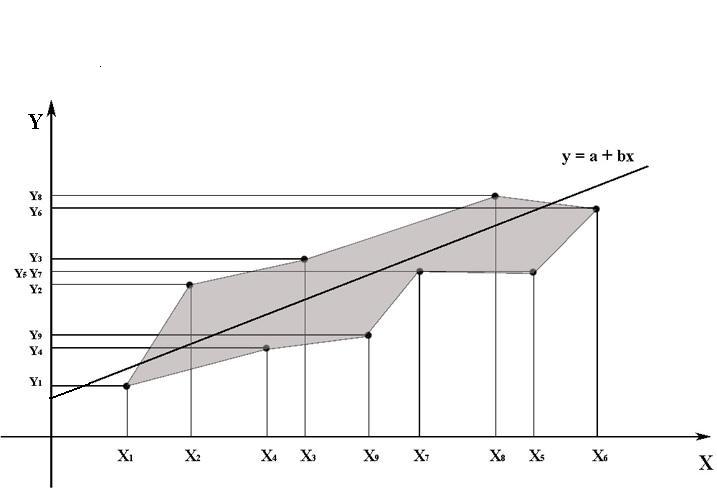
Рис. 8.1. Зависимость численности персонала (Y) от фактора Х.

Аналитическое выражение кривой при однофакторной линейной зависимости (Y = a + b*X) определяется решением системы уравнений:

,

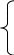
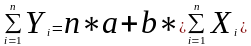
где X_i – i-е численное значение фактора;

Y_i – i-е значение численности;

n – количество анализируемых базовых предприятий;

a,b – искомые параметры уравнения регрессии.

При нелинейном характере зависимости фактора и численности нормативная формула может иметь вид:

Y = a*X^b

Y= a + b*lnX

Y = a + b/X и др

Достоинствами графоаналитического метода являются его наглядность и простота. Однако этот метод не учитывает взаимосвязи факторов, влияющих на численность, и в целом не обеспечивает достаточно строгого обоснования нормативной зависимости.

В случае, если выявлено влияние нескольких факторов на численность персонала, для установления параметров многофакторной зависимости целесообразно применять метод множественной корреляции. Обработка данных с помощью данного метода имеет следующие преимущества:

• позволяет разрабатывать нормативные зависимости от большого количества факторов;

• выявлять зависимости от отдельных факторов, причем при анализе не требуется постоянных значений других факторов;

• дает возможность измерить степень влияния отдельных факторов.

Применение данного метода основано на предположении, что влияние факторов на численность персонала в рассматриваемом случае имеет вид:

Y = А₀ + А₁Х₁ + А₂Х₂+ А₃Х₃ + ….

где А₀,А₁,А₂,А₃– искомые параметры уравнения регрессии, определяемые исходя из принципа наименьших квадратов.

В данном случае выражение имеет вид:

Q = ∑[Y – (А₀ + А₁Х₁ + А₂Х₂+ А₃Х₃ + ….)]² → min

Как известно, минимум функции можно найти, приравняв к нулю ее первые производные по А₀,А₁,А₂,А₃. Таким образом, получается система нормальных уравнений:

kА₀ + А₁∑Х₁ + А₂∑Х₂+ А₃∑Х₃ = ∑Y

А₀∑Х₁ + А₁∑Х₁² + А₂∑Х₁Х₂+ А₃∑Х₁Х₃ = ∑Х₁ Y

А₀∑Х₂ + А₁∑Х₁Х₂ + А₂∑Х₂²+ А₃∑Х₂Х₃ = ∑Х₂Y

А₀∑Х₃ + А₁∑Х₁Х₃ + А₂∑Х₂ Х₃+ А₃∑Х₃² = ∑Х₃ Y,

где к – количество анализируемых базовых предприятий;

А₀,А₁,А₂,А₃– искомые параметры системы.

Решить данную систему можно методом Крамера, т.е. А_i = ∆i/∆:

А₀= ∆0/∆

А₁= ∆1/∆

А₂ = ∆2/∆

А₃ = ∆3/∆,

где А₀,А₁,А₂,А₃– искомые параметры системы;

∆ – определитель системы;

∆i – алгебраические дополнения системы, получаемые из определителя ∆ заменой соответствующего i-го столбца столбцом свободных членов системы.

Решив данную систему уравнений и определив коэффициенты А₀,А₁,А₂,А₃ определяется аналитическое выражение норматива зависимости.