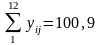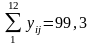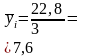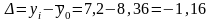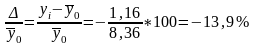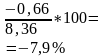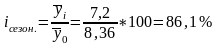Измерение сезонных колебаний

Уровни ряда колеблются под воздействием постоянно действующих факторов, случайных и периодических действующих сезонных факторов, которые вызывают сезонные колебания.

Сезонными колебаниями называются устойчивые, повторяющиеся из года в год колебания уровней ряда в одни и те же периоды года. Для каждого явления может быть свой период сезонных колебаний.

Изучение сезонных колебаний вызывается необходимостью исключения их влияния на общую динамику и для выявления чистой (случайной) колеблемости.

Изучение сезонных колебаний производится в следующей последовательности:

1. Устанавливается факт наличия сезонных колебаний (используется графический метод; строится график на основе помесячных данных за 3 года);

2. Измеряют сезонную волну при помощи индексов сезонности.

3. Анализ и прогнозирование внутригодичных колебаний осуществляется методом построения модели сезонных колебаний- гармоники ряда Фурье.

Методы измерения сезонных колебаний

1. Метод абсолютных разностей;

2. Метод относительных разностей;

3. Построение индексов сезонности

4. Расчет средних квадратических отклонений

При изучении сезонных колебаний необходимо использовать данные за ряд лет, чтобы исключить возможность смешивания случайных колебаний с сезонными.

Пример 7. Имеются помесячные данные за три года о перевозках пассажиров в пригородном

сообщении, млн. чел.

1	2	3	4	5	6
№ строки	Год	январь	……………….	декабрь	Итого за все месяцы года
1	1	7,2	……………….	7,7
2	2	7,3	……………….	7,5
3	3	7,1	……………..	7,6
4	Итого за весь период	21,6	………………	22,8	=301,0
5	Средний месячный уровень
6	Абсолютное отклонение			7,7- 8,36= =-0,66
7	Относительное отклонение
8	Индекс сезонности

Используя индексы сезонности, корректируют ряд динамики: 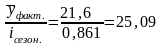; (средний январский уровень).

Для сравнения сезонных колебаний по нескольким объектам или нескольким периодам, может быть использовано среднее квадратическое отклонение, рассчитываемое по формуле: . Чем меньше эта величина, тем меньше размер сезонных колебаний.

Корреляция в рядах динамики

При изучении явления за определенный период, возникает необходимость оценить степень взаимодействия в изменениях уровней двух динамических рядов различного содержания, но связанных между собой. Например, оценить связь между стоимостью основных производственных фондов и объемом выпускаемой продукции. В этом случае прибегают к корреляции динамических рядов.

Для большинства динамических рядов существует определенная тенденция развития явления – тренд. Однако, согласно одной из основных предпосылок теории корреляции, является наличие независимости отдельных наблюдений. В силу этого, возникает необходимость освободится от влияния тренда, что бы более точно определить тесноту связи между явлениями.

Рассмотрим некоторые новые понятия.

1)Наличие зависимости между последовательными и предыдущими уровнями динамического ряда называются автокорреляцией. Она возникает в силу наличия тренда. Для освобождения от влияния тренда рассчитываются новые ряды, состоящие из отклонений последующего уровня от предыдущего, т.е. ; .

2)При сопоставлении уровней двух динамических рядов, необходимо учитывать наличие лага, т.е. смещение во времени изменения уровней одного ряда по сравнению с изменением уровней другого ряда. Например, если в этом году (месяце) были введены новые основные фонды, то это, может сказаться на увеличение выпуска продукции в следующем периоде (месяце, году). Поэтому возникает необходимость, сдвигать уровни одного ряда относительно уровней другого ряда , на определенный период месяц, год).

3) На разных отрезках времени изучаемого периода, условия формирования уровней могли серьезно измениться. В этом случае возникает переменная корреляция, т.е. изменяется во времени степень тесноты связи.

При применении методов корреляции в динамических рядах необходимо:

1. Измерить связь между последовательными уровнями одного и того же динамического ряда, для каждого ряда в отдельности. Таким образом, исчисляются коэффициенты автокорреляции и авторегрессии в каждом ряду, показывающие зависимость между последовательными уровнями ряда.

Автокорреляция- корреляционная зависимость между последовательными значениями уровней динамического ряда.

Авторегрессия- это регрессия, учитывающая влияние предыдущих уровней динамического ряда на последующие. При этом, находятся уравнение, связывающие исходные уровни динамического ряда с теми же уровнями, но сдвинутыми на некоторый период времени. Например, 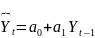.Коэффициенты автокорреляции вычисляются по непосредственным данным ряда динамики, когда фактические уровни одного ряда рассматриваются как значения факторного признака, а уровни этого же ряда со сдвигом на один период принимаются в качестве результативного признака. Коэффициент автокорреляции рассчитывается на основе формулы коэффициента корреляции для парной зависимости.

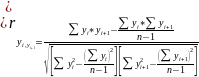
При обнаружении наличия автокорреляции в уровнях исходных рядов, то не следует коррелировать непосредственно уровни сравниваемых временных рядов, необходимо предварительно исключить автокорреляцию

Существуют несколько способов исключения автокорреляции. Один из них связан с корреляцией отклонений фактических уровней от тренда, т.е. .

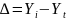При коррелировании отклонений фактических уровней от выравненных необходимо:

1)Произвести аналитическое выравнивание сопоставляемых рядов динамики.

2)Определить величину отклонения каждого фактического уровня ряда от соответствующего ему выравненного значения.

3)Рассчитать коэффициенты корреляции по полученным отклонениям.

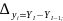
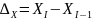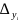К аналогичному результату можно прийти при оценке степени тесноты связи рядов динамики, если коррелировать разности между последующими и предыдущими уровнями, т.е. рассчитав величины , где и - абсолютные приросты с переменной базой в рядах динамики показателей Y и X.

Коэффициенты корреляции первых разностей рассчитывается по формуле:

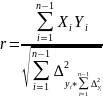
Следует помнить, что исключение автокорреляции с использованием данной формулы возможно только в тех рядах, где изменение уровней ряда можно охарактеризовать уравнением прямой.

16