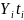Средние характеристики ряда динамики.

В качестве обобщающих показателей динамики, исследуемого явления, определяют средние показатели динамического ряда. Эти показатели можно разделить на две группы:

а) средние уровни ряда; б) средние показатели изменения уровней ряда.

Для интервального ряда абсолютных показателей средний уровень ряда определяется по формуле простой средней арифметической, т.е. , n- число уровней ряда.

Средний уровень моментного ряда с равными промежутками между датами, определяется по формуле средней хронологической:

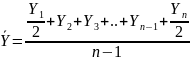
Для определения среднего уровня моментного ряда с неравными промежутками между датами, применяется средняя арифметическая взвешенная. В качестве весов берется продолжительность промежутков времени между моментами, в которые происходят изменения в уровнях динамического ряда. При этом, если указано, что изменение произошло первого числа месяца, то измененная стоимость фондов или другого явления учитывается в данном месяце. Во всех других случаях изменения начинают учитываться со следующей даты.

, где 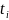- количество дней, месяцев между датами.

Пример 4. На 01.01. отчетного года стоимость основных фондов предприятия составила 4,0 млн. руб. В мае было введено основных фондов на 0,5млн. руб., в июле выбыло основных фондов на 0.8млн. млн. руб. , в октябре введено основных фондов на 0,3 млн. руб. Определить среднегодовую стоимость основных фондов предприятия.

Дата	Стоимость основных фондов,	Число месяцев, в течение которых эти фонды функционировали,
01.01	4,0	5	20,0
01.06	4,5	2	9,0
01.08	3,7	2	7,4
01.10	4,0	3	12,0
Итого		12	48,4

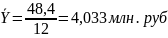-средняя стоимость основных фондов.

Следующий показатель- средний абсолютный прирост( средняя скорость роста)

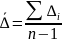, где n- число уровней ряда; -абсолютные приросты, рассчитанные с переменной базой.

Так как тогда = 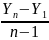, где и 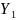- начальный и конечный уровень ряда.

Средний коэффициент роста вычисляется по формуле средней геометрической из показателей коэффициентов роста за отдельные периоды

, где 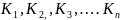- коэффициенты роста с переменной базой, а n- число уровней ряда.

Так как 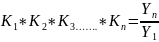, то средний коэффициент роста можно вычислить по формуле: = .

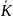При отсутствии данных о числе уровней в ряду, но имеются коэффициенты роста, расчет среднего коэффициента роста производится по формуле: = ,

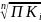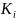-коэффициенты роста; П- знак произведения коэффициентов роста; n- число сомножителей (коэффициентов).

Средний темп роста – это средний коэффициент роста, выраженный в процентах:

; средний темп прироста -

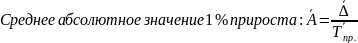
Выявление основной тенденции развития явления в динамических рядах.

Основная тенденция развития называется трендом. Для выявления тренда производят выравнивание временного ряда, при этом используются различные методы.

Методы механического сглаживания

1. Укрупнение интервала динамического ряда. Данный метод заключается в том, что первичный ряд преобразуется и заменяется другим, показатели которого относятся к большим по продолжительности периодам времени. Новые уровни ряда получают либо путем суммирования уровней ряда, либо вычислением средних уровней за укрупненный временной интервал. При этом отклонения в уровнях ряда, вызванные случайными причинами взаимно погашаются, сглаживаются и более ясно обнаруживается общая тенденция развития явления.

Рассмотрим нахождение переменной средней по укрупненным интервалам.

Пример 5. Имеются данные о стоимости продукции предприятия за 12 месяцев.

Месяц	Выпуск продукции, тыс. руб.	Суммы за квартал	Средняя квартальная
Январь	336
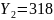
Февраль		1005,0	335,0
Март	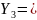349
Апрель	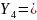330
Май	358	1041,0	347,0
Июнь	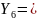353
Июль
Август	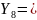371	1079,0	≈360
Сентябрь	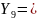357
Октябрь	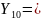356
Ноябрь	359	1076	≈359
Декабрь

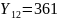
Нахождение переменной средней по укрупненным интервалам:

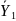= и т.д.

При использование этого метода теряется значительное число данных, поэтому его можно применять для анализа временных рядов с большим числом уровней ряда.