2.2.2. Метод аналитических группировок
Задание выполняем на основе данных таблицы 2.1 , а также дополнительных вспомогательных таблиц.
Чтобы выявить зависимость между исследуемыми показателями с помощью метода аналитических группировок, необходимо провести группировку единиц совокупности по факторному признаку x (количество перевезенного груза) и для каждой группы найти среднюю величину результативного признака y (прибыль от перевозок). Для формирования аналитических групп необходимо определить величину интервала значений факторного признака для каждой группы. Находим эту величину по следующей формуле:
(2.13)
где - максимальное значение ;
- минимальное значение ;
– число
аналитических групп.
Находим величину интервала для четырех групп:
.
Полученные группы представлены в таблице 2.4
Таблица 2.4
Вспомогательная таблица
№ |
Интервалы по факторному признаку |
Группы по Факторному Признаку |
Середины интервалов |
Группы по результативн. Признаку |
Объем группы |
Среднее значение результативн.
признака,
|
|||||||
M |
|||||||||||||
1 |
0,216-0,39 |
0,216 0,362 |
0,289+ |
|
2 |
0,614 |
|||||||
2 |
0,39-0,565 |
0,402 0,468 0,471 0,487 |
0,457 |
|
4 |
0,494 |
|||||||
3 |
0,565-0,739 |
0,581 0,591 |
0,586 |
|
2 |
0,628 |
|||||||
4 |
0,739-0,914 |
0,807 0,842 0,842 0,91 0,956 0,914 |
0,853 |
|
7 |
0,666 |
|||||||
Итого |
|
|
|
|
|
|
Также в таблице 2.4 рассчитано среднее значение результативного признака, которое вычисляется по формуле:
(2.14)
где - число уровней ряда.
Эмпирический коэффициент детерминации определяется по формуле:
,
(2.15)
где
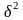- межгрупповая дисперсия;
-
общая дисперсия.
Межгрупповая дисперсия рассчитывается по формуле:
(2.16),
где
- число единиц в
-й
группе,
-
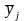среднее значение признака в j-ой группе.
Средние значения результативного признака по каждой группе были рассчитаны ранее и сведены в таблицу 2.4.
Таким образом рассчитаем межгрупповую дисперсию.
Теперь рассчитаем общую дисперсию по формуле:
С помощью формулы (2.6) и полученных данных определяем эмпирический коэффициент детерминации. В результате получаем:
.
Теперь мы можем определить коэффициент корреляционного отношения, который равен:
(2.17)
Полученные группы представлены в таблице 2.5
Таблица 2.5
Вспомогательная таблица
№ |
Интервалы по факторному признаку |
Группы по Факторному Признаку |
Середины интервалов |
Группы по результативн. признаку |
Объем Группы |
Среднее значение результативн. признака,
|
M |
||||||
1 |
0,01-0,145 |
0,01 0,05 0,06 0,12 0,13 |
0,074 |
0,871 1,111 1,154 1,388 1,02
|
55 |
0,991 |
2 |
0,145-0,28 |
0,15 0,2 0,22 |
0,19 |
0,337 1,198 0,532 |
33 |
1,13 |
3 |
0,28-0,415 |
0,39 0,42 |
0,405 |
0,933 0,676 |
22 |
1,27 |
4 |
0,415-0,55 |
0,47 0,5 0,54 0,55 |
0,515 |
0,892 0,74 0,606 0,726 0,933 |
45 |
1,2 |
Итого |
|
|
|
|
|
|
Связь между признаками сильная.
Полученные группы представлены в таблице 2.6
Таблица 2.6
Вспомогательная таблица
№ |
Интервалы по факторному признаку |
Группы по Факторному признаку |
Середины интервалов |
Группы по результативн. признаку |
Объем группы |
Среднее значение результативн. признака,
|
M |
||||||
|
0,264-0,426 |
0,264 0,362 0,402 |
0,342 |
0,47 0,15 0,59 |
3 |
0,403
|
2 |
0,426-0,586 |
0,468 0,471 0,581 |
0,475 |
0,54 0,55 0,5 |
3 |
0,53 |
3 |
0,586-0,751 |
0,591 0,703 |
0,586 |
0,42 0,39 |
2 |
0,405 |
4 |
0,751-0,914 |
0,703 0,807 0,842 0,842 0,91 0,956 0,914 |
0,853 |
0,06 0,13 0,22 0,2 0,05 0,12 0,01 |
7 |
0,112 |
Итого |
|
|
|
|
15 |
|
Связь между признаками прямая и сильная.
2.2.3. Метод корреляционно-регрессионного анализа
Построим 2 уравнения (линейное и нелинейное) парной корреляции.
Линейное уравнение парной корреляции (уравнение прямой) имеет следующий вид:
.
Для нахождения параметров и составим следующую систему нормальных уравнений:
Как
видно из системы для ее решения не
хватает
и
.
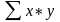Поэтому составляем вспомогательную
таблицу 2.7.
Таблица 2.7
Вспомогательная таблица
№ |
х |
У |
х2 |
х*у |
|||
1 |
2 |
3 |
4 |
5 |
|||
1 |
0,216 |
0,892 |
0,19267 |
0,19267 |
|||
2 |
0,362 |
0,337 |
0,12199 |
0,12199 |
|||
3 |
0,402 |
0,651 |
0,2617 |
0,2617 |
|||
4 |
0,468 |
0,606 |
0,28361 |
0,28361 |
|||
5 |
0,471 |
0,726 |
0,34195 |
0,34195 |
|||
6 |
0,487 |
0,74 |
0,36038 |
0,36038 |
|||
7 |
0,581 |
0,676 |
0,39276 |
0,39276 |
|||
8 |
0,591 |
0,933 |
0,5514 |
0,5514 |
|||
9 |
0,703 |
1,154 |
0,81126 |
0,81126 |
|||
10 |
0,807 |
1,02 |
0,82314 |
0,82314 |
|||
11 |
0,842 |
0,532 |
0,44794 |
0,44794 |
|||
12 |
0,842 |
1,198 |
1,00872 |
1,00872 |
|||
13 |
0,91 |
1,111 |
1,01101 |
1,01101 |
|||
14 |
0,956 |
1,388 |
1,32693 |
1,32693 |
|||
15 |
0,914 |
0,871 |
0,79609 |
0,79609 |
|||
Итого |
11,552 |
15,835 |
12,73156 |
13,73156 |
|||
По
полученным данным из таблицы получаем
систему нормальных уравнений:
Решая систему уравнений, получаем следующие значения параметров:
Подставляя полученные значения параметров, получаем уравнение прямой:
.
Подставляя значения в уравнение прямой, получаем следующие значения в таблице 2.6
Таблица 2.6
Расчетные значения результативного признака
№ |
Х |
y |
1 |
0,216 |
0,98486 |
2 |
0,362 |
0,98632 |
3 |
0,402 |
0,98672 |
4 |
0,468 |
0,98738 |
5 |
0,471 |
0,98741 |
6 |
0,487 |
0,98757 |
7 |
0,581 |
0,98851 |
8 |
0,591 |
0,98861 |
9 |
0,703 |
0,98973 |
10 |
0,807 |
0,99077 |
11 |
0,842 |
0,99112 |
12 |
0,842 |
0,99112 |
13 |
0,91 |
0,9918 |
14 |
0,956 |
0,99226 |
15 |
0,914 |
0,99184 |
Итого |
9,552 |
14,836 |
В качестве нелинейного уравнения регрессии возьмем квадратичное (уравнение параболы), которое имеет следующий вид:
.
Для нахождения параметров , и составим следующую систему нормальных уравнений:
.
Как
видно из системы для ее решения не
хватает
,
и
.
Поэтому составляем вспомогательную
таблицу 2.7
Таблица 2.7
-
№
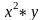
1
0,216
0,04666
0,002
0,17
2
0,362
0,13104
0,017
0,04
3
0,402
0,1616
0,026
0,17
4
0,468
0,21902
0,048
0,17
5
0,471
0,22184
0,049
0,25
6
0,487
0,23717
0,056
0,27
7
0,581
0,33756
0,114
0,27
8
0,591
0,34928
0,122
0,51
9
0,703
0,49421
0,244
0,94
10
0,807
0,65125
0,424
0,84
11
0,842
0,70896
0,503
0,24
12
0,842
0,70896
0,503
1,21
13
0,91
0,8281
0,686
1,12
14
0,956
0,91394
0,835
1,84
15
0,914
0,8354
0,698
0,69
∑
9,552
6,845
4,327
8,73
По полученным данным из таблицы получаем систему нормальных уравнений:
Решая данную систему уравнений, получаем следующие значения параметров:
Подставляя полученные значения параметров, получаем уравнение прямой:
Подставляя значения в уравнение прямой, получаем следующие значения в таблице 2.8.
Таблица 2.8
Расчетные значения результативного признака
№ |
Х |
У |
1 |
0,216 |
0,568097 |
2 |
0,362 |
0,6149 |
3 |
0,402 |
0,72237 |
4 |
0,468 |
0,775572 |
5 |
0,471 |
0,812108 |
6 |
0,487 |
0,832814 |
7 |
0,581 |
0,909286 |
8 |
0,591 |
1,009767 |
9 |
0,703 |
1,232547 |
10 |
0,807 |
1,302909 |
11 |
0,842 |
1,100968 |
12 |
0,842 |
1,434627 |
13 |
0,91 |
1,477377 |
14 |
0,956 |
1,693344 |
15 |
0,914 |
1,351936 |
ИтогоИтого |
11,552 |
15,83862 |
Для
того чтобы сделать вывод о том, какое
аналитическое уравнение (прямая или
парабола) наилучшим образом отражает
зависимость между исследуемыми
показателями, определим, для какого
уравнение значение
наименьшее.
Для этого составим вспомогательную
таблицу 2.9.
Таблица 2.9
Квадраты отклонений
№ |
для прямой |
для параболы |
1 |
0,009 |
0,1 |
2 |
0,422 |
0,08 |
3 |
0,113 |
0,01 |
4 |
0,145 |
0,03 |
5 |
0,068 |
0,01 |
6 |
0,061 |
0,01 |
7 |
0,098 |
0,05 |
8 |
0,003 |
0,01 |
9 |
0,027 |
0,01 |
10 |
9E-04 |
0,08 |
11 |
0,211 |
0,32 |
12 |
0,043 |
0,06 |
13 |
0,014 |
0,13 |
14 |
0,157 |
0,09 |
15 |
0,015 |
0,23 |
Итого |
1,3856 |
1,217 |
Так как для уравнения параболы сумма квадратов отклонений эмпирических ( ) значений от теоретических ( ) меньше, то уравнение параболы лучше описывает зависимость между исследуемыми показателями по сравнению с уравнением параболы.
Таблица 2.7
Вспомогательная таблица
№ |
Х |
У |
х2 |
х*у |
Y |
|
|
|
У |
|||||||||
1 |
0,01 |
0,871 |
0,008 |
0,00871 |
0,9828 |
0,0001 |
1E-08 |
0,01 |
0,754268 |
|||||||||
2 |
0,05 |
1,111 |
0,05555 |
0,05555 |
0,9832 |
0,0025 |
6E-06 |
0,06 |
0,806482 |
|||||||||
3 |
0,06 |
1,154 |
0,06924 |
0,06924 |
0,9833 |
0,0036 |
1E-05 |
0,08 |
0,820714 |
|||||||||
4 |
0,12 |
1,388 |
0,16656 |
0,16656 |
0,9839 |
0,0144 |
2E-04 |
0,23 |
0,915135 |
|||||||||
5 |
0,13 |
1,02 |
0,1326 |
0,1326 |
0,984 |
0,0169 |
3E-04 |
0,14 |
0,901015 |
|||||||||
6 |
0,15 |
0,337 |
0,05055 |
0,05055 |
0,9842 |
0,0225 |
5E-04 |
0,02 |
0,864367 |
|||||||||
7 |
0,2 |
1,198 |
0,2396 |
0,2396 |
0,9847 |
0,04 |
0,002 |
0,29 |
1,007282 |
|||||||||
8 |
0,22 |
0,532 |
0,11704 |
0,11704 |
0,9849 |
0,0484 |
0,002 |
0,06 |
0,946531 |
|||||||||
9 |
0,39 |
0,933 |
0,36387 |
0,36387 |
0,9866 |
0,1521 |
0,023 |
0,34 |
1,196857 |
|||||||||
10 |
0,42 |
0,676 |
0,28392 |
0,28392 |
0,9869 |
0,1764 |
0,031 |
0,19 |
1,167544 |
|||||||||
11 |
0,47 |
0,892 |
0,41924 |
0,41924 |
0,9874 |
0,2209 |
0,049 |
0,37 |
1,27849 |
|||||||||
12 |
0,5 |
0,74 |
0,37 |
0,37 |
0,9877 |
0,25 |
0,063 |
0,27 |
1,26745 |
|||||||||
13 |
0,54 |
0,606 |
0,32724 |
0,32724 |
0,9881 |
0,2916 |
0,085 |
0,2 |
1,266352 |
|||||||||
14 |
0,55 |
0,726 |
0,3993 |
0,3993 |
0,9882 |
0,3025 |
0,092 |
0,29 |
1,315314 |
|||||||||
15 |
0,59 |
0,651 |
0,38409 |
0,38409 |
0,9886 |
0,3481 |
0,121 |
0,25 |
1,330608 |
|||||||||
|
6,4 |
15,835 |
7,38751 |
8,38751 |
15,835 |
1,89 |
0,468 |
2,8 |
15,83841 |
|||||||||
Таблица 2.9
Квадраты отклонений
№ |
для прямой |
для параболы |
1 |
0,012 |
0,01 |
2 |
0,016 |
0,09 |
3 |
0,029 |
0,11 |
4 |
0,163 |
0,22 |
5 |
0,001 |
0,01 |
6 |
0,419 |
0,28 |
7 |
0,045 |
0,04 |
8 |
0,205 |
0,17 |
9 |
0,003 |
0,07 |
10 |
0,097 |
0,24 |
11 |
0,009 |
0,15 |
12 |
0,061 |
0,28 |
13 |
0,146 |
0,44 |
14 |
0,069 |
0,35 |
15 |
0,114 |
0,46 |
Итого |
|
|
Так как для уравнения параболы сумма квадратов отклонений эмпирических ( ) значений от теоретических ( ) больше, то уравнение прямой лучше описывает зависимость между исследуемыми показателями по сравнению с уравнением параболы.
№ |
Х |
У |
х2 |
х*у |
y |
|
|
|
У |
||||||||
1 |
0,264 |
0,47 |
0,12408 |
0,12408 |
0,4526 |
0,264 |
0,0697 |
0,005 |
0,43534 |
||||||||
2 |
0,362 |
0,15 |
0,0543 |
0,0543 |
0,4623 |
0,362 |
0,1310 |
0,017 |
0,404405 |
||||||||
3 |
0,402 |
0,59 |
0,23718 |
0,23718 |
0,4663 |
0,402 |
0,1616 |
0,026 |
0,51753 |
||||||||
4 |
0,468 |
0,54 |
0,25272 |
0,25272 |
0,4728 |
0,468 |
0,2190 |
0,048 |
0,53391 |
||||||||
5 |
0,471 |
0,55 |
0,25905 |
0,25905 |
0,4731 |
0,471 |
0,2214 |
0,049 |
0,53800 |
||||||||
6 |
0,487 |
0,5 |
0,2435 |
0,2435 |
0,4747 |
0,487 |
0,237 |
0,056 |
0,53047 |
||||||||
7 |
0,581 |
0,42 |
0,24402 |
0,24402 |
0,4840 |
0,581 |
0,3375 |
0,114 |
0,54094 |
||||||||
8 |
0,591 |
0,39 |
0,23049 |
0,23049 |
0,4850 |
0,591 |
0,3492 |
0,122 |
0,53397 |
||||||||
9 |
0,703 |
0,06 |
0,04218 |
0,04218 |
0,4961 |
0,703 |
0,4942 |
0,244 |
0,43402 |
||||||||
10 |
0,807 |
0,13 |
0,10491 |
0,10491 |
0,5063 |
0,807 |
0,6512 |
0,424 |
0,48257 |
||||||||
11 |
0,842 |
0,22 |
0,18524 |
0,18524 |
0,5098 |
0,842 |
0,7089 |
0,503 |
0,53415 |
||||||||
12 |
0,842 |
0,2 |
0,1684 |
0,1684 |
0,5986 |
0,842 |
0,7089 |
0,503 |
0,52413 |
||||||||
13 |
0,91 |
0,05 |
0,0455 |
0,0455 |
0,516 |
0,91 |
0,8281 |
0,686 |
0,45835 |
||||||||
14 |
0,956 |
0,12 |
0,11472 |
0,11472 |
0,5211 |
0,956 |
0,9139 |
0,835 |
0,50450 |
||||||||
15 |
0,914 |
0,01 |
0,00914 |
0,00914 |
0,5169 |
0,914 |
0,8354 |
0,698 |
0,43715 |
||||||||
|
11,6 |
7,4 |
6,31543 |
7,31543 |
7,4 |
9,6 |
6,8680 |
4,33 |
7,40948 |
||||||||
Таблица 2.9
Квадраты отклонений
№ |
для прямой |
для параболы |
1 |
3E-04 |
0 |
2 |
0,098 |
0,06 |
3 |
0,015 |
0,01 |
4 |
0,005 |
0 |
5 |
0,006 |
0 |
6 |
6E-04 |
0 |
7 |
0,004 |
0,01 |
8 |
0,009 |
0,02 |
9 |
0,19 |
0,14 |
10 |
0,142 |
0,12 |
11 |
0,084 |
0,1 |
12 |
0,096 |
0,11 |
13 |
0,218 |
0,17 |
14 |
0,161 |
0,15 |
15 |
0,257 |
0,18 |
Итого |
1,2849 |
1,073 |
Так как для уравнения параболы сумма квадратов отклонений эмпирических ( ) значений от теоретических ( ) меньше, то уравнение параболы лучше описывает зависимость между исследуемыми показателями по сравнению с уравнением параболы.
Теперь построим уравнение множественной регрессии, которое отражает связь между результативным и несколькими факторными признаками. Уравнение множественной регрессии имеет вид:
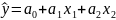
Для нахождения параметров , и составим следующую систему нормальных уравнений:
.
Для решения системы составим вспомогательную таблицу 2.16
Таблица 2.16
№ |
У |
х1 |
х2 |
х1 кв |
х2 кв |
х1х2 |
х1у |
х2у |
1 |
0,871 |
0,914 |
0,01 |
0,835 |
0,0001 |
0,09 |
0,796 |
0,087 |
2 |
1,388 |
0,956 |
0,12 |
0,913936 |
0,0144 |
0,11472 |
1,326928 |
0,16656 |
3 |
1,111 |
0,91 |
0,05 |
0,8281 |
0,0025 |
0,0455 |
1,01101 |
0,05555 |
4 |
1,02 |
0,807 |
0,13 |
0,651249 |
0,0169 |
0,10491 |
0,82314 |
0,1326 |
5 |
0,651 |
0,402 |
0,59 |
0,161604 |
0,3481 |
0,23718 |
0,261702 |
0,38409 |
6 |
0,74 |
0,487 |
0,5 |
0,237169 |
0,25 |
0,2435 |
0,36038 |
0,37 |
7 |
0,532 |
0,842 |
0,22 |
0,708964 |
0,0484 |
0,18524 |
0,447944 |
0,11704 |
8 |
0,337 |
0,362 |
0,15 |
0,131044 |
0,0225 |
0,0543 |
0,121994 |
0,05055 |
9 |
0,606 |
0,468 |
0,54 |
0,219024 |
0,2916 |
0,25272 |
0,283608 |
0,32724 |
10 |
0,892 |
0,264 |
0,47 |
0,069696 |
0,2209 |
0,12408 |
0,235488 |
0,41924 |
11 |
0,933 |
0,531 |
0,39 |
0,281961 |
0,1521 |
0,20709 |
0,495423 |
0,36387 |
12 |
1,154 |
0,703 |
0,06 |
0,494209 |
0,0036 |
0,04218 |
0,811262 |
0,06924 |
13 |
0,726 |
0,471 |
0,55 |
0,221841 |
0,3025 |
0,25905 |
0,341946 |
0,3993 |
14 |
1,098 |
0,842 |
0,2 |
0,708964 |
0,04 |
0,1684 |
0,924516 |
0,2196 |
15 |
0,676 |
0,581 |
0,42 |
0,337561 |
0,1764 |
0,24402 |
0,392756 |
0,28392 |
Сумма |
11,864 |
8,626 |
4,39 |
5,965322 |
1,8899 |
2,28289 |
7,838097 |
3,3588 |
Решая систему получаем значения параметров:
Получаем уравнение множественной корреляции:
ПО полученному уравнению рассчитаем теоретические значения ( таблица 2.17):
Таблица 2.17
-
№
1
1,005701
2
1,028018
3
1,003574
4
0,948851
5
0,733627
6
0,778804
7
0,967492
8
0,712412
9
0,768715
10
0,660303
11
0,802222
12
0,893617
13
0,770325
14
0,967444
15
0,828793
Сумма
11,8642