3. Выборочное наблюдения

_{Выборочное наблюдение будем проводить на основе данных таблицы 1.19}

_{Таблица 1.19}

_{Данные о длительности рейса судов}

№ рейса	Длительность рейса
1	147
2	138
3	134
4	130
5	128
6	126
7	136
8	129
9	137
10	139
11	117
12	112
13	114
14	129
15	198
16	189
17	111
18	218
19	242
20	187
21	196
22	191
23	199
24	225
25	230
26	178
27	171
28	177
29	184
30	188
31	200
32	210
33	165
34	166
35	174
36	156
37	175
38	177
39	173
40	176
41	255
42	156

1.4.1. Случайная бесповторная выборка

Проведем случайную бесповторную выборку с объемом выборки равной 32 единицам. Для этого создадим выборочную совокупность из 32 произвольно выбранных единиц, а затем представим ее в виде следующей таблицы 1.20

Таблица 1.20

Случайная бесповторная выборка

№ рейса	Длительность рейса, сутки
1	111
2	112
3	114
4	117
5	126
6	128
7	129
8	129
9	130
10	134
11	136
12	137
13	139
14	147
15	156
16	156
17	165
18	166
19	171
20	175
21	177
22	177
23	176
24	184
25	188
26	189
27	199
28	200
29	210
30	225
31	230
32	255
	Итого: 5188

Определим среднюю величину при случайной бесповторной выборке, которая находится по формуле:

(1.45)

где - дисперсия;

- объем выборочной совокупности;

- объем генеральной совокупности.

Прежде чем определить среднюю величину найдем дисперсию, находится по формуле простой дисперсии ,так как нам не известны удельные веса показателей, которые изучаются:

(1.46).

Для дисперсии найдем по формуле 1.4.2 Будем искать простую среднюю так как не известны удельные веса изучаемых показателей.

(1.47).

Таким образом,

соответственно и

1220,015

Теперь можно определить среднюю величину, которая равна

Найдем предельную ошибку репрезентативности случайной бесповторной выборки при определении средней величины по следующей формуле:

(1.48),

где - коэффициент доверия, который зависит от вероятности , с которой гарантируется значение предельной ошибки выборки.

Так как , то .

Таким образом, предельная ошибка репрезентативности случайной бесповторной выборки при определении средней величины :

.

Далее рассчитаем относительную ошибку выборки, которая вычисляется по формуле:

(1.49)

Теперь можно найти границы, в которых находится генеральная средняя по формуле:

(1.50),

.

Таким образом, с вероятностью 0,954 можно утверждать, что продолжительность рейса находится в пределах от 158,4 до 165,8 суток.

Признаком для определения долей будет продолжительность рейса меньше 170 суток.

Далее определим долю судна в выборочной совокупности (выборочную долю) по формуле:

(1.51),

где - выборочная доля, которую можно найти по следующей формуле:

(1.52),

где - число единиц выборочной совокупности, которые владеют признаком, который изучается.

В данном случае признаку соответствуют 18 судов.

Таким образом, .

Теперь можно определить выборочную долю

Найдем предельную ошибку репрезентативности случайной бесповторной выборки при определении доли по следующей формуле:

(1.53),

где - коэффициент доверия, который зависит от вероятности , с которой гарантируется значение предельной ошибки выборки.

Так как , то .

Таким образом, предельная ошибка репрезентативности случайной бесповторной выборки при определении доли равна 0,036 или 3,6%.

Далее рассчитаем относительную ошибку выборки, которая вычисляется по формуле:

(1.54)

Теперь можно найти границы, в которых находится доля по формуле:

(1.55),

_,

Таким образом, с вероятностью 0,954 можно утверждать, что доля судна с продолжительностью рейса меньше 170 суток находится в пределах от 56% до 64%.

3.2 Типическая бесповторная выборка

Проведем типическую бесповторную выборку с объемом 32 единиц. Для этого сначала сформируем 4 выборочных группы. Для формирования групп определим величину интервала каждой группы по формуле:

(1.56),

где l – число групп.

Таким образом, .

Таким образом получаем 4 интервала и их частоты:

1. 111-147 (13);

2. 147-183 (9)

3. 183-219 (6);

4. 219-255 (3).

Группы типической выборки, как правило, неравные по объему; рекомендуется проводить отбор пропорционально численности групп:

, (1.57)

где n_j – объем выборки из п-ой группы;

N_j – объем j-ой группы по генеральной совокупности;

N – объем генеральной совокупности;

n – объем выборки.

Исходя из этой пропорции, численности групп типической выборки будут составлять:

;

Сформируем таблицу 1.21 по данным типической выборки.

Таблица 1.21

Типическая бесповторная выборка

Интервалы	111-147	147-183	183-219	219-255
Состав группы	111 112 114 117 126 128 129 129 130 134 136 137 139	147 156 156 165 166 171 175 177 176	184 188 189 199 200 210	225 230 255
Объем выб-х групп	13	9	6	3
Гр.выб-я средняя	126,3	165,4	195	236,6
	232,3	338,6	121	134,56
	204,7	88,36	49	43,56
	151,5	88,36	36	338,56
	86,6	0,16	16
	0,09	0,36	25
	2,8	31,36	225
	7,2	92,16
	13,69	134,56
	59,29	112,36
	114,5
	161,3
Гр.выб-я дисперсия для средней	15,3	9,97	10,26	12,78
	1	0,55	0	0
	0	0,45	1	1

Теперь рассчитаем среднюю ошибку репрезентативности типической бесповторной выборки при определении средней величины по следующей формуле:

. (1.58)

Сначала находим групповые дисперсии по формуле:

; j = . (1.59)

Средние по каждой группе типической выборки определяются по следующей формуле:

. (1.60)

Затем находим групповые дисперсии для средней (таблица 3.3)

Теперь найдем среднюю из групповых дисперсий по формуле:

(1.70)

Найдем предельную ошибку репрезентативности типической бесповторной выборки :

(1.71),

где - коэффициент доверия, который зависит от вероятности , с которой гарантируется значение предельной ошибки выборки.

Так как , то .

Таким образом, предельная ошибка репрезентативности случайной бесповторной выборки при определении средней величины :

.

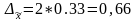Далее рассчитаем относительную ошибку выборки, которая вычисляется по формуле:

(1.72)

(1.73)

Теперь можно найти границы, в которых находится генеральная средняя по формуле:

(1.74),

.

Вывод: с вероятностью 0,954 можно утверждать, что средняя продолжительность рейса находится в пределах от 182,62 до 183,94 суток.

Теперь найдем долю судов в группах типической бесповторной выборки с продолжительностью рейса меньше 17

0 суток по формуле:

, (1.77)

где - количество судов в j-ой группе типической бесповторной выборки с продолжительностью рейса меньше 170 суток., число единиц в j-ой группе.

Пример расчета за первый период:

.

Средняя доля судов в группах типической бесповторной выборки вычисляется по формуле:

(1.78)

Теперь находим среднюю из групповых дисперсий по следующей формуле:

(1.79)

Теперь рассчитаем среднюю ошибку репрезентативности типической бесповторной выборки при определении доли по следующей формуле:

, (1.80)

_.

Рассчитаем предельную ошибку репрезентативности типической бесповторной выборки при определении доли по следующей формуле:

, (1.81)

_.

Далее рассчитаем относительную ошибку выборки, которая вычисляется по формуле:

(1.82)

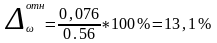
Теперь найдем границы, в которых находится доля, по формуле:

. (1.83)

0,58-0,076 p 0,58+0,076;

0,504 p _0,656

В процентном отношении это неравенство будет иметь такой вид:

50,4% p _65,6%

Вывод: с вероятностью 0,954 можно утверждать, что доля рейсов с продолжительностью меньше 170 суток для всех судов находится в пределах от 50,4% до 65,6%.