3. Наблюдение статистических рядов распределения

Исходной базой для расчета является таблица 1.14.

Таблица 1.14

№	Брутто-регистровая вместитеность, тыс. т	Количество суден
1	12-14	18
2	14-16	14
3	16-18	11
4	18-20	5
5	20-22	7
6	22-24	3
7	24-26	9

В ходе данной части задания необходимо рассчитать среднее значение, моду и медиану.

1. Расчет средних величин

Для расчета среднего значения будем использовать среднее арифметическое взвешенное, так как для каждого интервала имеется удельный вес – то есть количество судов.

Средневзвешенное арифметическое определим по формуле:

_(1.25)

где - середина интервала,

m – количество судов на каждом интервале.

(тыс. т)

Моду рассчитаем по формуле:

, (1.26)

где - нижняя граница, или начало, модального интервала,

- величина модального интервала,

, , - соответственно частота модального, предмодального и постмодального интервалов.

Модальный интервал 12-14 т.к. он имеет наибольшую частоту 18.

(тыс.т)

Таким образом, в ряду наиболее часто встречается значение 15 тыс. т.

Для расчета медианы необходимо определить медианный интервал. В интервальном ряду медианный интервал будет равен значению признака в той единице совокупности, для которой кумулятивная частота равна или превышает половину объема совокупности:

Объем совокупности равен 67, ее половина – 33,5. Таким образом, медианный интервал – 14-16 с кумулятивной частотой 32.

Конкретное значение медианы рассчитывается по формуле:

, (1.27)

где - нижняя граница медианного интервала;

- величина медианного интервала;

- частота медианного интервала;

- кумулятивная частота предмедианного интервала.

(тыс.т.)

2. Определение показателей вариации

Для выполнения дальнейших расчетов составим вспомогательную таблицу 1.15.

Таблица 1.15

Вспомогательная таблица

№	Х	m	Xm	Ix-x ̅I	Ix-x ̅I*m	(x-x ̅)2	(x-x ̅)2*m	x2
1	13	18	234	13	-234	169	3042	169
2	15	14	210	15	210	225	3150	225
3	17	11	187	17	187	289	3179	289
4	19	5	95	19	95	361	1805	361
5	21	7	147	21	147	441	3087	441
6	23	3	69	23	69	529	1587	529
7	25	9	225	25	225	625	5625	625
Σ		67	1167	133	699	2639	21475	2639

Размах вариации:

, (1.28)

где - максимальное количество партий

- минимальное количество партий;

_R=25-13=12.

Среднее линейное отклонение, которое вычисляется по формуле:

; (1.29)

Дисперсия:

(1.30)

320,5

17,9

Коэффициент вариации:

, (1.31)

где - среднее квадратическое отклонение.

102,7%

Коэффициент осцилляции:

, (1.32)

где R – размах вариации;

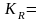68,9%

Относительное линейное отклонение:

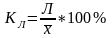, (1.33)

где, Л – среднее линейное отклонение;

59,9%

Из вышеприведенных расчетов можно сделать вывод, что совокупность не однородна, а ее репрезентативность – низкая.