
- •1. Анализ результатов производственно-финансовой деятельности судоплавной компании
- •1.2 Анализ динамики показателей
- •1.2.1 Показатели динамики
- •Наблюдение статистических рядов распределения
- •Расчет средних величин
- •Определение показателей вариации
- •1.3.3. Изучение формы распределения
- •Графическое изображение ряда распределения
- •Выборочное наблюдения
- •1.4.1. Случайная бесповторная выборка
- •Анализ статистических индексов
- •1.5.1. Построение агрегатных индексов
- •Индексный факторный анализ
- •Статистические методы изучения взаимосвязей между признаками
- •2.1 Общая характеристика показателей
- •2.2.2. Метод аналитических группировок
- •2.2.4 Оценка силы корреляционной связи
- •2.2.5 Построение гистограмм отклонений эмпирических значений от теоретическиих
1.2 Анализ динамики показателей
Оценку показателей динамики и выявление тенденций динамики будем проводить на основе табл. 1.2.
Таблица 1.1
Динамика грузооборота
Показатели |
1год |
2год |
3год |
4год |
5год |
6год |
7год |
Отправлено груза, тыс.т |
20560 |
21185 |
22635 |
23768 |
25261 |
25210 |
25426 |
Начислено доходов, млн.ден.ед. |
767,8 |
783,4 |
853,9 |
917,7 |
962,9 |
1013,1 |
1063 |
1.2.1 Показатели динамики
Выполним расчет базисных и цепных показателей динамики для всех семи лет и сведем их в единую таблицу 1.2 и 1.3. При расчете базисных показателей за базисный будем принимать первый год.
Абсолютный прирост определяется как разница между двумя уровнями ряда и характеризирует абсолютную меру изменения признака , что изучается, со временем.
Базисный абсолютный прирост будем вычислять по формуле:
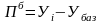 ,
(1.1)
,
(1.1)
где
 - количество перегруженных грузов в
текущем году,
- количество перегруженных грузов в
текущем году,
 -
количество перегруженных грузов в
базовом году;
-
количество перегруженных грузов в
базовом году;
Для первого года абсолютный прирост равен 0 так как первый год является базовым.
Цепной абсолютный прирост будем вычислять по формуле:
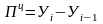 ,
(1.2)
,
(1.2)
где
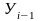 - количество перегруженных грузов в
предыдущем году.
- количество перегруженных грузов в
предыдущем году.
Для первого года показатель абсолютного прироста рассчитывать не будем, так как не имеем значения предшествующего года.
Темп роста определяется как отношение двух уровней, что сравниваются. Он показывает, в сколько раз поточный уровень больше (меньше) базисного или какую его часть занимает.
Базисный темп роста будем вычислять по формуле:
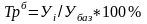 ;
(1.3)
;
(1.3)
За первый год темп роста равен 100%, так как он же является базовым.
Цепной темп роста будем вычислять по формуле:
 . (1.4)
. (1.4)
Темп прироста показывает, сколько единиц абсолютного прироста приходится на единицу базисного уровня.
Базисный темп прироста будем вычислять по формуле:
 ;
(1.5)
;
(1.5)
де
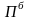 - абсолютный прирост базисный.
- абсолютный прирост базисный.
Цепной темп прироста будем вычислять по формуле:
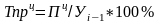 ,
(1.6)
,
(1.6)
где
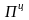 - абсолютный прирост цепной.
- абсолютный прирост цепной.
Абсолютное значение 1% прироста; дает общую характеристику интенсивности динамики.
Базисное значение будем вычислять по формуле:
 ;
(1.7)
;
(1.7)
Цепное значение будем вычислять по формуле:
 .
(1.8)
.
(1.8)
Все данные сводим в табл. 1.2 и табл.1.3.
Таблица 1.2
Показатели динамики по отправленному грузу, тыс.т.
Года Показатели |
Вид показателя |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Абсолютный прирост, тыс. т |
Базовый |
0 |
625 |
2075 |
3208 |
4701 |
4650 |
4866 |
Цепной |
- |
625 |
1450 |
1133 |
1493 |
51 |
216 |
|
Темп роста, % |
Базовый |
100 |
103,1 |
110,1 |
115,6 |
122,8 |
122,6 |
123,6 |
Цепной |
- |
103,1 |
106,8 |
105,1 |
106,3 |
99,8 |
100,8 |
|
Темп прироста, % |
Базовый |
0 |
3,1 |
10,1 |
15,6 |
22,8 |
22,6 |
23,7 |
Цепной |
0 |
3,1 |
6,8 |
5,1 |
6,3 |
-0,2 |
0,85 |
|
Абсолютное значение 1% прироста |
Базовый |
205,6 |
205,6 |
205,6 |
205,6 |
205,6 |
205,6 |
205,6 |
Цепной |
- |
205,6 |
211,8 |
226,3 |
237,6 |
252,6 |
252,1 |
Таблица 1.3
Показатели начисленных доходов, млн.ден.ед.
Года Показатели |
Вид показателя |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Абсолютный прирост, тыс. т |
Базовый |
0 |
15,6 |
86,1 |
149,9 |
195,1 |
245,3 |
295,2 |
Цепной |
- |
15,6 |
70,5 |
63,8 |
45,2 |
50,2 |
49,9 |
|
Темп роста, % |
Базовый |
100 |
102,3 |
111,2 |
119,5 |
125,4 |
131,9 |
138,4 |
Цепной |
- |
102,3 |
108,9 |
107,5 |
104,9 |
105,2 |
104,9 |
|
Темп прироста, % |
Базовый |
0 |
2,1 |
11,2 |
19,4 |
25,4 |
31,9 |
38,4 |
Цепной |
- |
2,1 |
8,9 |
7,4 |
4,9 |
5,2 |
4,9 |
|
Абсолютное значение 1% прироста |
Базовый |
7,7 |
7,7 |
7,7 |
7,7 |
7,7 |
7,7 |
7,7 |
Цепной |
- |
7,7 |
7,8 |
8,5 |
9,1 |
9,6 |
9,6 |
Средний уровень ряда рассчитывается по формуле:
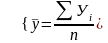 ,
(1.9)
,
(1.9)
где у – показатели грузооборота,
n - количество показателей грузооборота.
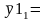 164045тыс.
т – средний уровень ряда для количества
отправленного груза
164045тыс.
т – средний уровень ряда для количества
отправленного груза
 6361,8
млн.ден.ед- средний уровень ряда для
количества начисленных доходов.
6361,8
млн.ден.ед- средний уровень ряда для
количества начисленных доходов.
Средний абсолютный прирост рассчитываем по формуле:
 ,
(1.10)
,
(1.10)
где n – количество годов, исключая базисный.
П1=4866 тыс.т
П2=141,1 млн.ден.ед.
Средний темп роста вычисляем по формуле:
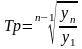 .
(1.11)
.
(1.11)
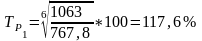
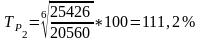
Средний темп прироста вычисляем по формуле:
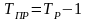 (1.12)
(1.12)

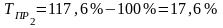
Существует взаимосвязь между базисными и цепными показателями динамики. Покажем эту взаимосвязь.
Сумма всех цепных абсолютных отклонений равна последнему базисному абсолютному отклонению.
 ;
;
625+1450+1133+1493+51+216=4650;
4650=4650.
15,6+70,5+63,8+45,2+50,2+49,9=295,2
295,2=295,2
Между цепными и базисными темпами роста существует такая связь:
а) произведение цепных темпов роста приводит к получению какого-то базисного. Например:
 ;
(1.13)
;
(1.13)

115,6=115,6.

119,5=119,5.
б) произведение всех цепных темпов роста равно последнему базисному темпу роста:
 ;
(1.14)
;
(1.14)
1,03*1,06*1,05*1,06*99,8*1,008=1,23
1,23=1,23.
1,02*1,08*1,07*1,04*1,05*1,04=1,32
1,32=1,32.
в) деление базисных темпов роста приводит к какому-то цепному темпу роста. Например:
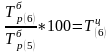 ;
(1.15)
;
(1.15)

99,8=99,8.

102,5=102,5.
Вывод:
Таким образом, проанализировав динамику Q, можно сделать вывод.
По сравнению с 1 годом в 6 и 7 году наблюдался рост грузооборота соответственно на 4701тыс.т. и 4650 тыс.т. или на 22,6% и 23,6%, а в 2 году наблюдался наименьший рост грузооборота.
В среднем в течении рассмотренного 7-летнего периода наблюдался ежегодный рост грузооборота на 2543,2 тыс.т., или на 15,2%.
По сравнению с 1 годом грузооборот в 6 и 7 году наблюдался рост начислений доходов соответственно на 245,3 млн.ден.ед. и 295,2 млн.ден.ед. на 31,9% и 384%, во 2 году наблюдался наименьший рост начислений.
В среднем в течении рассмотренного 7-летнего периода наблюдался ежегодный рост грузооборота на 141,02 млн.ден.ед, или на 25,8%.
1.2.2 Выявление тенденции динамики
Далее проанализируем тенденцию динамики, применив прием сглаживания с помощью скользящей средней. Подвижная средняя определяется как средняя арифметическая простая и относится к середине периода, за который она рассчитывается.
Полученные результаты расчета представлены в таблице 1.4 и 1.5.
Скользящая средняя:
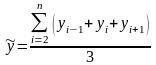 ,
(1.17)
,
(1.17)
Пример вычисления за второй год:
ỹ2 =(20560+21185+22635)/3=45310.
Показатели скользящего среднего рассчитаны и сведены в таблицу 1.4 и 1.5.
Таблица 1.4
Расчет скользящего среднего
Года
Показатели |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Q, тыс. т |
20560 |
21185 |
22635 |
23768 |
25261 |
25210 |
25426 |
Перемещаемая трехлетняя масса |
- |
64380 |
67588 |
71664 |
74239 |
75897 |
- |
Скользящее среднее |
|
21460 |
22529,3 |
23888 |
24746,3 |
25299 |
|
Таблица 1.5
Расчет скользящего среднего
Года
Показатели |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Q, млн.ден.ед. |
767,8 |
783,4 |
853,9 |
917,7 |
962,9 |
1013,1 |
1063,0 |
Перемещаемая трехлетняя масса |
- |
2405,1 |
2555 |
2734,5 |
2893,7 |
3039 |
- |
Скользящее среднее |
|
801,7 |
851,667 |
911,5 |
964,567 |
1013 |
|
Проведем аналитическое выравнивание ряда по прямой. Уравнение прямой имеет следующий вид:
 ;
;
Для нахождения параметров а0 и а1 составим следующую системы нормальных уравнений:
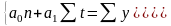
Как
видно из системы для ее решения не
хватает
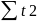 и
и
 ,
потому составляем вспомогательную
таблицу 1.6 и 1.7.
,
потому составляем вспомогательную
таблицу 1.6 и 1.7.
Таблица 1.6
Вспомогательная таблица
t |
t2 |
Y |
t*y |
1 |
1 |
20560 |
1087,7 |
2 |
4 |
21185 |
1080,7 |
3 |
9 |
22635 |
1383,6 |
4 |
16 |
23768 |
1728,1 |
5 |
25 |
25261 |
2083,9 |
6 |
36 |
25210 |
3053,7 |
7 |
49 |
25426 |
3555,6 |
Итого: 28 |
140 |
164045 |
4377,8 |
Таблица 1.7
Вспомогательная таблица
t |
t2 |
Y |
t*y |
1 |
1 |
767,8 |
1087,7 |
2 |
4 |
783,9 |
1080,7 |
3 |
9 |
853,9 |
1383,6 |
4 |
16 |
917,7 |
1728,1 |
5 |
25 |
962,9 |
2083,9 |
6 |
36 |
1013,1 |
6078,6 |
7 |
49 |
1063 |
3555,6 |
Итого: 28 |
140 |
6362,3 |
4377,8 |
По полученным данным их таблицы составляем систему нормальных уравнений:
7а0+28а1 = 164045,
28а0+140а1 = 4377,8;
Решая данную систему уравнений получаем следующий значения параметров:
а0=19952,
а1=870,75;
Подставляя полученные значения параметров, получим уравнение прямой:
 =
19952+870,75*t
(1.20)
=
19952+870,75*t
(1.20)
Связь между количеством перегруженных грузов и периодом времени прямая.
Подставляем значения времени t в полученное уравнение 1.20. Полученные результаты заносим в таблицу 1.7.
Таблица 1.7
Теоретические значения Q
T |
Y |
1 |
20822,8 |
2 |
21693,5 |
3 |
22564,3 |
4 |
23435 |
5 |
24305,8 |
6 |
25176,5 |
7 |
26047,3 |
Итого |
164045 |
Аналогичные операции проделаем и для значений начисленных доходов, полученные результаты занесем в таблицу 1.8.
Таблица 1.8.
Теоритические значения Q
T |
Y |
1 |
488,075 |
2 |
628,35 |
3 |
768,625 |
4 |
908,9 |
5 |
1049,18 |
6 |
1189,45 |
7 |
1329,73 |
Итого |
6362,3 |
Прогноз изучаемого показателя на следующий год:
 8=
19952+870,75=26918
(тыс. т.)
8=
19952+870,75=26918
(тыс. т.)
8= 347,8+140,275*8=1470(тыс. т.)
Проведем аналитическое выравнивание ряда по параболе. Уравнение параболы имеет следующий вид:
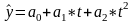 .
.
Для
нахождения параметров
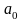 ,
,
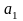 и
и
 составим
следующую систему нормальных уравнений:
составим
следующую систему нормальных уравнений:
 .
.
Как
видно из системы для ее решения не
хватает
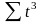 ,
,
 и
и
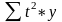 .
Поэтому составляем вспомогательную
таблицу 1.9 и 1.10.
.
Поэтому составляем вспомогательную
таблицу 1.9 и 1.10.
Таблица 1.9
Вспомогательная таблица
T |
t2 |
t3 |
t4 |
Y |
t*y |
t2*y |
1 |
1 |
1 |
1 |
20560 |
1087,7 |
20560 |
2 |
4 |
8 |
16 |
21185 |
1080,7 |
84740 |
3 |
9 |
27 |
81 |
22635 |
1383,6 |
203715 |
4 |
16 |
64 |
256 |
23768 |
1728,1 |
380288 |
5 |
25 |
125 |
625 |
25261 |
2083,9 |
631525 |
6 |
36 |
216 |
1296 |
25210 |
3053,7 |
907560 |
7 |
49 |
343 |
2401 |
25426 |
3555,6 |
1245874 |
Итого |
140 |
784 |
4676 |
164045 |
4377,8 |
3474262 |
Таблица 1.10
Вспомогательная таблица
T |
t2 |
t3 |
t4 |
Y |
t*y |
t2*y |
1 |
1 |
1 |
1 |
767,8 |
1087,7 |
767,8 |
2 |
4 |
8 |
16 |
783,9 |
1080,7 |
3135,6 |
3 |
9 |
27 |
81 |
853,9 |
1383,6 |
7685,1 |
4 |
16 |
64 |
256 |
917,7 |
1728,1 |
14683,2 |
5 |
25 |
125 |
625 |
962,9 |
2083,9 |
24072,5 |
6 |
36 |
216 |
1296 |
1013,1 |
6078,6 |
36471,6 |
7 |
49 |
343 |
2401 |
1063 |
3555,6 |
52087 |
Итого |
140 |
784 |
4676 |
6362,3 |
4377,8 |
138903 |
По полученным данным из таблицы 1.9 получаем систему нормальных уравнений:

Решая данную систему уравнений, получаем следующие значения параметров:
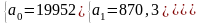 .
.
Подставляя полученные значения параметров, получаем уравнение прямой:
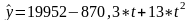 .
.
Полученные расчеты и прогноз на следующий год представлены в таблице 1.11.
Таблица 1.11
Теоретические значения Q
T |
t2 |
Y |
1 |
1 |
20835,3 |
2 |
4 |
21692,6 |
3 |
9 |
22562,9 |
4 |
16 |
23433,2 |
5 |
25 |
24303,5 |
6 |
36 |
25173,8 |
7 |
49 |
26044,1 |
Итого: 28 |
140 |
164045 |
Прогноз изучаемого показателя на следующий год:
 26914,4
(тыс. т.)
26914,4
(тыс. т.)
Аналогично получаем показатель на следующий год для показателей начисленных доходов
328,7 (тыс. т.)
Аналитическое
выравнивание (прямая или парабола)
описывает лучше тенденцию динамики в
том случае, когда сумма квадратов
отклонений эмпирических данных (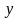 )
от теоретических (
)
от теоретических (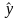 )
приближается к своему минимальному
значению (
)
приближается к своему минимальному
значению ( ).
Полученные расчеты представлены в
таблице 1.12 и 1.13.
).
Полученные расчеты представлены в
таблице 1.12 и 1.13.
Таблица 1.12
Квадраты отклонений
T |
|
для параболы |
1 |
69063,84 |
75790,09 |
2 |
258572,3 |
257657,8 |
3 |
4998,49 |
5198,41 |
4 |
110889 |
112091 |
5 |
912407 |
916806,3 |
6 |
1122,25 |
1310,44 |
7 |
386013,7 |
382047,6 |
Итого |
1743067 |
1750902 |
Так как для уравнения параболы сумма квадратов отклонений эмпирических данных ( ) от теоретических ( ) больше, чем для уравнения прямой, то уравнение прямой лучше описывает тенденцию динамики.
Сделаем интервальный прогноз, который рассчитывается по следующей формуле:
 (1.21)
(1.21)
где
 - прогнозируемое значение;
- прогнозируемое значение;
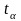 -
коэффициент доверия по распределению
Стьюдента (в таблице);
-
коэффициент доверия по распределению
Стьюдента (в таблице);
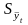 -
остаточное среднеквадратическое
отклонение от тренда, скорректированное
по числу степеней свободы (n-m),
которое находится по формуле:
-
остаточное среднеквадратическое
отклонение от тренда, скорректированное
по числу степеней свободы (n-m),
которое находится по формуле:
 (1.22)
(1.22)
 =80,
=80,
 .
.
Таким
образом,
 .
.
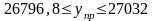 .
.
Таким образом, можно утверждать, что прогнозируемое значение 26796,8 тыс.т. и не более 27030тыс.т.
Таблица 1.13
Квадраты отклонений
T |
для прямой |
для параболы |
1 |
78246,08 |
695 |
2 |
24195,8 |
116 |
3 |
7271,826 |
173 |
4 |
77,44 |
242 |
5 |
7444,238 |
32 |
6 |
31099,32 |
410 |
7 |
71144,89 |
510 |
Итого |
219479,6 |
1611 |
Так как для уравнения параболы сумма квадратов отклонений эмпирических данных ( ) от теоретических ( ) меньше, чем для уравнения прямой, то уравнение параболы лучше описывает тенденцию динамики.
Сделаем интервальный прогноз, который рассчитывается по следующей формуле:
(1.23)
где - прогнозируемое значение;
- коэффициент доверия по распределению Стьюдента (в таблице);
- остаточное среднеквадратическое отклонение от тренда, скорректированное по числу степеней свободы (n-m), которое находится по формуле:
(1.24)

 .
.
Таким
образом,
 .
.
Таким образом, можно утверждать, что прогнозируемое значение 331,3 тыс.т. и не более 331,3тыс.т.
На основании данных (исходных и полученных), построим эмпирическую, сглаженную и теоретическую линии (рисунок 1.1).
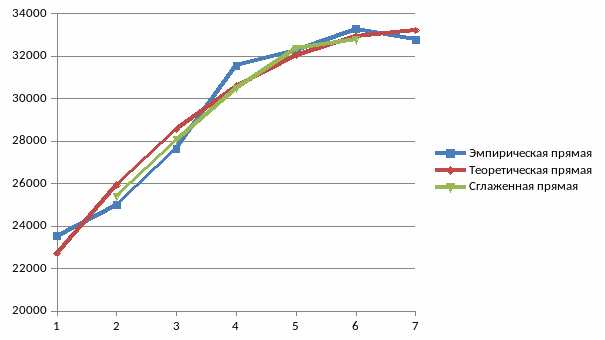
Рис. 1.1 Тенденции динамики

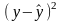 для
уравнения прямой
для
уравнения прямой