Задача №40

З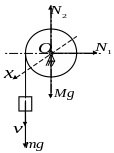 образимо барабан з віссю обертання . Будемо розглядати рух системи, до якої входять вантаж, барабан та нитка. Зображуємо сили, що діють на цю систему – це сили ваги барабана , тіла та реакції в’язі (шарніра ) . Використаємо теорему про зміну кінетичного моменту системи: , де – кінетичний момент системи відносно осі , – момент зовнішніх сил, прикладених до системи, відносно осі . Задаємо вектор швидкості тіла.

Кінетичний момент системи дорівнює , де , - кінетичні моменти відносно осі барабана та тіла відповідно. Маємо, , , де - радіус блока. Таким чином, , а , де - прискорення тіла.

Знайдемо момент . Моменти реакцій в’язей відносно осі дорівнюють нулеві, тому що ці в’язі перетинають вісь. Момент створюють сили ваги: .

Маємо , тобто м/с².

Відповідь: 5 м/с².

Задача №41

Будемо розглядати рух кульки. Зобразимо сили, що на неї діють – це сила ваги та натяг нитки . Використаємо теорему про зміну кінетичної енергії точки: , де Т, Т₀ – кінетична енергія та початкова кінетична енергія відповідно, А – робота сил. При максимальному відхиленні нитки швидкість кульки дорівнює нулеві, тобто . В початковий момент маємо .

Робота натягу нитки дорівнює нулеві: . Роботу сили ваги знайдемо за формулою: , де - висота, на яку підніметься кулька. При горизонтальному положенні нитки ця висота дорівнює довжині нитки, тобто . Таким чином, маємо співвідношення: = , тобто м/с.

Відповідь: 6 м/с.

Задача №42

Зобразимо сили, що на неї діють на тіло – це сила ваги та натяг нитки . Використаємо теорему про зміну кінетичної енергії точки: , де Т, Т₀ – кінетична енергія та початкова кінетична енергія відповідно, А – робота сил. При максимальному відхиленні нитки швидкість кульки дорівнює нулеві, тобто . В початковий момент маємо . Робота натягу нитки дорівнює нулеві: . Роботу сили ваги знайдемо за формулою: , де - висота, на яку підніметься кулька. Маємо , де - кут відхилення нитки. Маємо співвідношення: = , тобто . знаходимо, .

Відповідь: .

Задача №43

Використаємо теорему про зміну кінетичної енергії твердого тіла: , де Т, Т₀ – кінетична енергія та початкова кінетична енергія відповідно, А – робота сил, прикладених до вантажу. Вантаж здійснює поступальний рух, тому його кінетична енергія має вираз . Початкова кінетична енергія дорівнює нулеві: . Робота прикладених сил дорівнює: м. Таким чином, маємо: м/с.

Відповідь: 3 м/с.

Задача №44

Використаємо теорему про зміну кінетичної енергії системи: , де Т, Т₀=0 – кінетична енергія системи та початкова кінетична енергія системи відповідно, – робота зовнішніх сил, прикладених до системи. Будемо розглядати рух системи, до якої входять вантажі, блок та нитка. Зображуємо сили, що діють на цю систему – сили ваги та реакції в’язі (шарніра ) . Задаємо вектор швидкості першого вантажу. Враховуючи, що вантажі здійснюють поступальний рух і , тобто , запишемо .

Знайдемо роботу зовнішніх сил, прикладених до системи. Робота реакцій в’язей дорівнює нулеві, тому що точка їх прикладення нерухома. Робота сил ваги дорівнює: . Таким чином, маємо співвідношення , з якого отримаємо

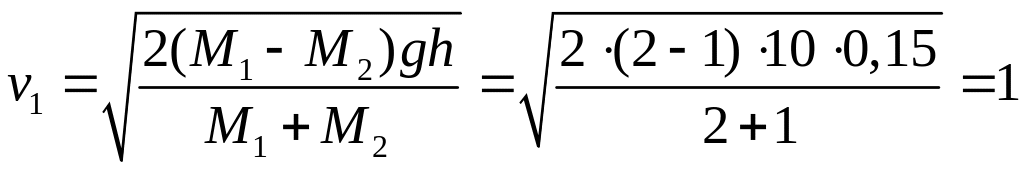м/с.

Відповідь: 1 м/с

Задача №45

Будемо розглядати рух тіла як матеріальної точки під дією сили ваги. Використаємо теорему про зміну кінетичної енергії системи: , де Т, Т₀ – кінетична енергія тіла та початкова кінетична енергія тіла відповідно, – робота сил, прикладених до тіла. Маємо , , тобто . Звідси знаходимо висоту падіння м.

Відповідь: 5 м.

Задача №46

Кінетичну енергію колеса будемо шукати за формулою , де – маса колеса, - швидкість центра мас колеса, - момент інерції колеса вдносно осі, що проходить через центр мас, - кутова швидкість колеса, - радіус колеса. Кутову швидкість знайдемо за формулою , де - відстань від точки до миттєвого цента швидкостей , який знаходиться в точці дотику колеса до поверхні. Будемо мати:

Відповідь: 5

Задача №47

Використаємо теорему про зміну кінетичної енергії тіла: , де Т, Т₀=0 – кінетична енергія тіла та початкова кінетична енергія тіла відповідно. Кінетичну енергія стержня будемо шукати за формулою , де - момент інерції стержня відносно осі обертання.

Сили, що діють на стержень – це реакції в точці підвісу та сила ваги . Робота реакцій дорівнює нулю, а робота сили ваги дорівнює - де - висота переміщення точки прикладення сили ваги. Маємо співвідношення . Звідси знаходимо

1/с.

Відповідь: 10 1/с.

Задача №48

Використаємо теорему про зміну кінетичної енергії твердого тіла: , де Т, Т₀ – кінетична енергія тіла та початкова кінетична енергія тіла відповідно, – робота зовнішніх сил, прикладених до тіла. Зображуємо сили, що діють на тіло – силу ваги та реакції в’язі (поверхні) та . Кінетичну енергію тіла, яке здійснює плоский рух, будемо знаходити за формулою , - швидкість центра мас, - осьовий момент інерції (R – радіус циліндра), - кутова швидкість тіла. Щоб знайти кутову швидкість, зобразимо миттєвий центр швидкостей , який знаходиться в точці дотику тіла до поверхні. Знаходимо: . Тоді . В початковий момент маємо . В кінцевому положенні .

Знайдемо роботу прикладених до тіла сил. Робота реакцій в’язей дорівнює нулеві, тому що вони прикладені в нерухомій точці - миттєвому центрі швидкостей. Робота сили ваги дорівнює . Із співвідношення знаходимо

м/с.

Відповідь: 2 м/с.

Задача №49

Будемо розглядати систему, до якої входять барабан, тіло та нитка. Кінетична енергія системи складається з кінетичних енергій барабана та вантажу. Тіло здійснює поступальний рух із швидкістю і його кінетична енергія дорівнює . Барабан здійснює обертальний рух навколо осі і його кінетична енергія дорівнює , де - осьовий момент інерції ( – радіус барабана), - кутова швидкість барабана. Щоб знайти кутову швидкість барабана, спочатку знайдемо швидкість точки - точки дотику нитки до барабана. Швидкість цієї точки, як точки нитки, що рухається поступально, дорівнює швидкості вантажу, тому маємо . Тоді кінетична енергія барабана буде . Кінетична енергія системи дорівнює .

Звідси знаходимо м/с.

Відповідь:3 м/с.