НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ

«Київський політехнічний інститут»

Факультет авіаційних і космічних систем

________________________________________

(назва факультету (інституту))

Ректорський контроль осінь ’ 2011 (розв’язки задач)

для студентів V курсу

Кафедра приладів та систем керування літальними апаратами

_______________________________________________________

(назва кафедри )

7.100104, 7.100101

____________________________________________________________

(код спеціальності)

«Системи керування літальними апаратами та комплексами»

«Літаки і вертольоти»

____________________________________________________________

(назва спеціальності)

Теоретична механіка

____________________________________________________________

(назва дисципліни)

професор Рижков Л.М., тел.406-83-17

____________________________________________________________

(розробник дисципліни ( ПІБ), конт. телефони)

Затверджую

Завідувач кафедри

_______________ ____Збруцький О.В.___

(підпис) (прізвище та ініціали)

Контактні телефони:_______________________

№ 1

Розглянемо рівновагу балки АЕ. Введемо систем координат Аxy. Звільняємо балку від в’язей та вводимо реакції в’язей: .

Для знаходження реакції стержня записуємо рівняння моментів відносно осі :

З цього рівняння знаходимо Н.

Відповідь: Н.

№ 2

Розглянемо рівновагу балки АВ. Введемо систем координат Аxy. Звільняємо балку від в’язей та вводимо реакції в’язей: .

Для знаходження реакції в опорі записуємо рівняння моментів відносно осі :

.

Знаходимо Н.

Відповідь: Н.

№ 3

Розглянемо рівновагу балки АВ з ниткою та вантажем. Введемо систем координат Вxy. Зображуємо силу . Звільняємо систему від в’язей та вводимо реакції в’язей: . Для знаходження реакцій записуємо рівняння моментів відносно осі :

Знаходимо Н.

Відповідь: Н.

№ 4

Розглянемо рівновагу балки АС з ниткою та вантажем. Введемо систем координат Аxy. Зображуємо силу . Звільняємо систему від в’язей та вводимо реакції в’язей: . Для знаходження реакцій записуємо рівняння моментів відносно осі

З першого рівняння знаходимо

З третього рівняння знаходимо Н.

З другого рівняння знаходимо

Відповідь: , , Н.

№ 5

Розглянемо рівновагу балки АС. Введемо систем координат Аxy.. Звільняємо систему від в’язей та вводимо реакції в’язей: . Для знаходження реакції в опорі С записуємо рівняння рівноваги – суму моментів відносно точки А:

З рівняння знаходимо

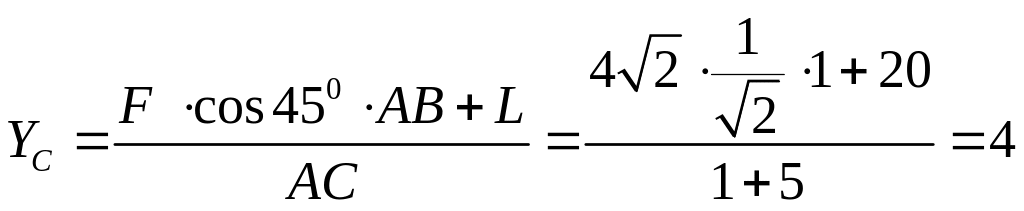Н.

Відповідь: Н.

№ 6

Р озглянемо рівновагу балки АВ. Введемо систему координат Аxy.. Звільняємо систему від в’язей і вводимо реакції в’язей: .

Для знаходження реакцій записуємо рівняння рівноваги балки:

З першого рівняння знаходимо

З другого рівняння знаходимо Н.

З третього рівняння знаходимо .

Відповідь: , Н, .

№ 7

Р озглянемо рівновагу балки АВ. Введемо систем координат Аxy.. Звільняємо систему від в’язей та вводимо реакції в’язей: .

Для знаходження моменту в защемленні А записуємо рівняння рівноваги балки – суму моментів відносно точки А:

З рівняння знаходимо

.

Відповідь: .

№ 8

Нормальне прискорення точки знаходиться за формулою , де - швидкість точки. За натуральним способом задання руху . Знаходячи , отримаємо . В момент часу маємо , в момент часу маємо . Тобто м/с².

Відповідь: 8 м/с².

№ 9

Прискорення точки знаходиться за формулою . Дотичне прискорення точки дорівнює . Нормальне прискорення точки дорівнює , де - швидкість точки. За натуральним способом задання руху . Знаходячи м/с, отримаємо м/с² . Прискорення точки дорівнює м/с².

Відповідь: м/с².

№ 10

Доосьове прискорення точки, яка знаходиться на відстані від точки до осі обертання, дорівнює , де - кутова швидкість обертання тіла, Доосьове прискорення точки, яка знаходиться на відстані від точки до осі обертання, дорівнює тому маємо . Якщо прийняти =2 м/с², м, м, то за цією формулою знаходимо м/с².

Відповідь: м/с².

№ 11

Обертальне прискорення точки в момент часу дорівнює , де - відстань від точки до осі обертання. Обертальне прискорення точки в момент часу дорівнює , тобто . Тому м/с².

Відповідь: м/с².

№ 12

Прискорення точки знаходиться за формулою . Обертальне прискорення точки дорівнює , де - кутове прискорення тіла, - відстань від точки до осі обертання. Доосьове прискорення точки дорівнює , де - кутова швидкість обертання тіла. Маємо м/с².

Відповідь: м/с².

№ 13

М иттєвий центр швидкостей шатуна АВ будемо знаходити на перетині перпендикулярів до напрямів швидкостей двох точок шатуна АВ. Швидкість точка А, яка належить також кривошипу ОА, буде перпендикулярна до кривошипа ОА. Проводимо пряму І₁І₁, перпендикулярну до вектора . Вектор швидкості точки В завжди напрямлений вздовж напрямних, які обмежують рух повзуна – проводимо пряму І₂І₂, перпендикулярну до напрямних. Перетин прямих І₁І₁ та І₂І₂ дає миттєвий центр швидкостей – точку Р, яка співпадає з точкою В. Тому м.

Відповідь: м.

Завдання № 14

Знайдемо миттєвий центр швидкостей колеса – він знаходиться в точці Р дотику колеса з поверхнею. Вектор точки В буде напрямлений перпендикулярно до прямої ВР в напрямі обертання колеса. Величину швидкості точки В знайдемо з пропорції , де R – радіус колеса. Тобто

м/c.

Відповідь: м/c.

Завдання № 15

Спочатку знайдемо миттєвий центр швидкостей шатуна АВ. Миттєвий центр швидкостей шатуна АВ будемо знаходити на перетині перпендикулярів до напрямів швидкостей двох точок шатуна АВ. Швидкість точка А, яка належить також кривошипу ОА, буде напрямлена перпендикулярно до кривошипа ОА в напрямі обертання кривошипа. Проводимо пряму І₁І₁, перпендикулярну до вектора . Вектор швидкості точки В завжди напрямлений вздовж напрямних, які обмежують рух повзуна – проводимо пряму І₂І₂, перпендикулярну до напрямних. Паралельні прямі І₁І₁ та І₂І₂ не перетинаються, тобто миттєвого центра швидкостей нема. Це означає що шатун АВ в цей момент часу здійснює миттєво-поступальний рух, за яким всі точки тіла мають однакові швидкості. Таким чином, . Швидкість точки А, як точки кривошипа ОА, що обертається навколо нерухомої осі, знайдемо за формулою м/c..Таким чином м/c.

Відповідь: м/c.

Завдання № 16

С початку знайдемо миттєвий центр швидкостей шатуна АВ. Миттєвий центр швидкостей шатуна АВ будемо знаходити на перетині перпендикулярів до напрямів швидкостей двох точок шатуна АВ. Швидкість точка А, яка належить також кривошипу ОА, буде напрямлена перпендикулярно до кривошипа ОА в напрямі обертання кривошипа. Проводимо пряму І₁І₁, перпендикулярну до вектора . Вектор швидкості точки В завжди напрямлений вздовж напрямних, які обмежують рух повзуна – проводимо пряму І₂І₂, перпендикулярну до напрямних. Паралельні прямі І₁І₁ та І₂І₂ не перетинаються, тобто миттєвого центра швидкостей нема. Це означає що шатун АВ в цей момент часу здійснює миттєво-поступальний рух, за яким кутова швидкість шатуна дорівнює нулеві.

Відповідь: .

Завдання № 17

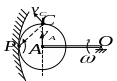
Шестерня здійснює плоский рух. Для визначення швидкості точки С знайдемо миттєвий центр швидкостей шестерні – він знаходиться в точці Р дотику шестерні до нерухомої поверхні. Далі знаходимо швидкість точки А, яка одночасно належить шестерні та кривошипу. Швидкість точки А напрямлена перпендикулярно до кривошипа в напрямі його обертання і дорівнює м/с. Зображуємо стрілкою напрям обертання шестерні навколо миттєвого центра швидкостей. Вектор швидкості точки С буде напрямлений перпендикулярно до відрізку РС в напрямі обертання шестерні, а величину швидкості точки С знайдемо з пропорції . Таким чином, маємо м/с.

Відповідь: м/c.

.

Завдання № 18

Маємо складний рух точки, за яким абсолютна швидкість точки дорівнює , де - переносна швидкість, - відносна швидкість. Переносна швидкість точки напрямлено перпендикулярно до ОМ в бік обертання тіла, а її величина дорівнює , де - кутова швидкість тіла, . В момент часу с маємо =1 м/c. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто до ободу диска, а її величина дорівнює м/c. Напрям вектора абсолютної швидкості визначається векторною сумою векторів переносної та відносної швидкостей. Напрями переносної та відносної швидкостей співпадають, тому величина абсолютної швидкості точки дорівнює м/c.

Відповідь: м/c.

Завдання № 19

М аємо складний рух точки, за яким абсолютна швидкість точки дорівнює , де - переносна швидкість, - відносна швидкість. Переносна швидкість точки напрямлено перпендикулярно до ОМ в бік обертання тіла, тобто від нас, а її величина дорівнює , де . В момент часу с маємо м/c. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої СВ, а її величина дорівнює 9 м/c. Напрям вектора абсолютної швидкості визначається векторною сумою векторів переносної та відносної швидкостей. Вектори переносної та відносної швидкостей взаємно перпендикулярі, тому величина абсолютної швидкості точки дорівнює м/c.

Відповідь: м/c.

Завдання № 20

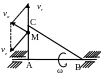
Маємо складний рух точки, за яким абсолютна швидкість точки дорівнює , де - переносна швидкість, - відносна швидкість. Переносна швидкість точки напрямлена перпендикулярно до АМ в бік обертання тіла, тобто до нас, а її величина в момент часу с дорівнює м/c. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж прямої АС, а її величина дорівнює м/c. Напрям вектора абсолютної швидкості визначається векторною сумою векторів переносної та відносної швидкостей. Вектори переносної та відносної швидкостей взаємно перпендикулярі, тому величина абсолютної швидкості точки дорівнює м/c.

Відповідь: м/c.

Завдання № 21

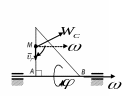
Прискорення Коріоліса точки визначається за формулою , де - кутова швидкість тіла, - відносна швидкість точки . Кутова швидкість дорівнює с^-1. Вектор кутової швидкості напрямлений вздовж осі обертання в напрямі обертання, що випливає з додатного значення кутової швидкості. Щоб знайти напрям прискорення Коріоліса, перенесемо вектор точку М. Вектор напрямлений так, що з кінця вектора найкоротший поворот вектора до вектора видно проти ходу годинної стрілки, тобто від нас. Модуль вектора дорівнює м/с².

Відповідь: м/с².

Завдання № 22

Прискорення Коріоліса точки визначається за формулою , де - кутова швидкість тіла, - відносна швидкість. Вектор кутової швидкості напрямлений вздовж осі обертання в напрямі обертання. Щоб знайти прискорення Коріоліса, перенесемо вектор точку М. Вектори та напрямлені вздовж однієї прямої, а в цьому випадку модуль вектора дорівнює . Таким чином, прискорення Коріоліса відсутнє.

Відповідь: .

Завдання № 23

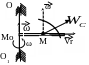
Прискорення Коріоліса точки визначається за формулою , де - кутова швидкість тіла, - відносна швидкість точки . Вектор кутової швидкості напрямлений вздовж осі обертання в напрямі обертання. Щоб знайти напрям прискорення Коріоліса, перенесемо вектор точку М. Відносна швидкість точки напрямлена по дотичній до траєкторії відносного руху, тобто вздовж трубки в напрямі руху, а її величина дорівнює м/c. Щоб знайти прискорення Коріоліса, перенесемо вектор точку М. Вектор напрямлений так, що з кінця вектора найкоротший поворот вектора до вектора видно проти ходу годинної стрілки, тобто від нас. Модуль вектора дорівнює м/с².

Відповідь: м/с².