19. Показательная функция и ее алгебраические свойства Пусть — неотрицательное вещественное число, — рациональное число: . Тогда определяется по следующим правилам.

• Если , то .

• Если и , то .

  • Значение не определено (см. Раскрытие неопределённостей).

• Если и , то .

  • Значение при не определено.

Для произвольного вещественного показателя значение можно определить как предел последовательности , где — рациональные числа, сходящиеся к . Для экспоненты есть и другие определения через предел, например:

Свойства

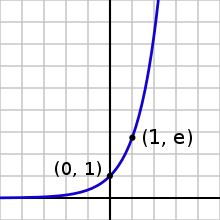
График экспоненты

• 

• 

• 

• 

Используя функцию натурального логарифма , можно выразить показательную функцию с произвольным положительным основанием через экспоненту:

Эта связь позволяет ограничиться изучением свойств экспоненты.

Аналитические свойства:

В частности:

Доказательство [скрыть]

I. Докажем, что

. Ч. т. д.

Докажем, что . Пусть , тогда . Если , то

II. Ч. т. д.

Разложение в ряд:

.

Асимптотика

Показательная функция растёт на бесконечности быстрее любой полиномиальной:

Большая скорость роста может быть проиллюстрирована, например, задачей о складывании бумаги.

20. Существование логарифмов.Логарифмическая функция и ее алгебраические свойства.

Логарифмическая функция обратна к показательной

Графики логарифмических функций

Основные характеристики

Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию . Она определена при . Область значений: . Эта кривая часто называется логарифмикой^[9]. Из формулы замены основания логарифма видно, что графики логарифмических функций с разными основаниями, бо́льшими единицы, отличаются один от другого только масштабом по оси ; графики для оснований, меньших единицы, являются их зеркальным отражением относительно горизонтальной оси.

Из определения следует, что логарифмическая зависимость есть обратная функция для показательной функции , поэтому их графики симметричны относительно биссектрисы первого и третьего квадрантов (cм. рисунок). Как и показательная, логарифмическая функция относится к категории трансцендентных функций.

Функция является строго возрастающей при (см. далее графики) и строго убывающей при . График любой логарифмической функции проходит через точку . Функция непрерывна и неограниченно дифференцируема всюду в своей области определения.

Ось ординат является левой вертикальной асимптотой, поскольку:

при

при .

Производная логарифмической функции равна:

С точки зрения алгебры, логарифмическая функция осуществляет (единственно возможный) изоморфизм мультипликативной группы положительных вещественных чисел и аддитивной группы всех вещественных чисел. Другими словами, логарифмическая функция есть единственное (определённое для всех положительных значений аргумента) непрерывное решение функционального уравнения^[10]:

Свойства

Основное логарифмическое тождество

Из определения логарифма следует основное логарифмическое тождество^[7]:

Следствие: из равенства двух вещественных логарифмов следует равенство логарифмируемых выражений. В самом деле, если , то , откуда, согласно основному тождеству:

огарифмы единицы и числа, равного основанию

Два равенства, очевидных из определения логарифма:

Логарифм произведения, частного от деления, степени и корня

Приведём сводку формул в предположении, что все значения положительны^[8]:

	Формула	Пример
Произведение
Частное от деления
Степень
Корень

Существует очевидное обобщение приведённых формул на случай, когда допускаются отрицательные значения переменных, например:

Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:

Вышеописанные свойства объясняют, почему применение логарифмов (до изобретения калькуляторов) существенно облегчало вычисления. Например, умножение многозначных чисел с помощью логарифмических таблиц^[⇨] производилось по следующему алгоритму:

1. Найти в таблицах логарифмы чисел .

2. Сложить эти логарифмы, получая (согласно первому свойству) логарифм произведения .

3. По логарифму произведения найти в таблицах само произведение.

Деление, которое без помощи логарифмов намного более трудоёмко, чем умножение, выполнялось по тому же алгоритму, лишь с заменой сложения логарифмов на вычитание. Аналогично упрощались возведение в степень и извлечение корня.