Часть 2. Пусть теперь неограниченна сверху. Это значит, что .

Но . Значит, и поэтому можно записать . Выбрасывая в этом неравенстве , получим окончательно

что и говорит о том, что .

14.Число е, и связанные с ним пределы.

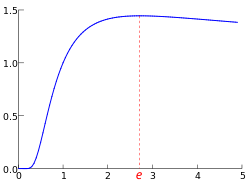
e — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».

Максимум функции достигается при .

Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики. Способы определения

Число e может быть определено несколькими способами.

• Через предел:

(второй замечательный предел).

• Как сумма ряда:

или .

• Через определённый интеграл:

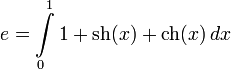
• Как единственное число a, для которого выполняется

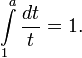
• Как единственное положительное число a, для которого верно

15.Непрерывность функции в точке. Непрерывность суммы, произведения и частного.

Непрерывность функции в точке.

Определение. Функция f(x), определенная в окрестности некоторой точки х₀, называется непрерывной в точке х₀, если предел функции и ее значение в этой точке равны, т.е.

Тот же факт можно записать иначе:

Определение. Если функция f(x) определена в некоторой окрестности точки х₀, но не является непрерывной в самой точке х₀, то она называется разрывной функцией, а точка х₀ – точкой разрыва.

Пример непрерывной функции:

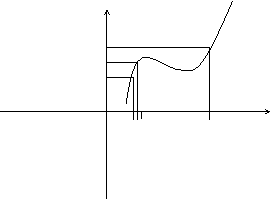y

f(x₀)+

f(x₀)

f(x₀)-

0 x₀- x₀ x₀+ x

Пример разрывной функции:

y

f(x₀)+

f(x₀)

f(x₀)-

x₀ x

Определение. Функция f(x) называется непрерывной в точке х₀, если для любого положительного числа >0 существует такое число >0, что для любых х, удовлетворяющих условию

верно неравенство .

Определение. Функция f(x) называется непрерывной в точке х = х₀, если приращение функции в точке х₀ является бесконечно малой величиной.

f(x) = f(x₀) + (x)

где (х) – бесконечно малая при хх₀.

Теоремы о непрерывности суммы, произведения, частного непрерывных функций, о непрерывности сложенных функций.

Теорема:

Сумма, произведение и частное двух непрерывных функций – непрерывны.

Доказательство:

Докажем для произведения.

Пусть . Тогда, по теореме о пределе произведения:

.

Теорема:

Пусть функция непрерывна в точке , а функция непрерывна в точке . Тогда сложная функция , состоящая из непрерывных функций, непрерывна в точке .

Доказательство:

Т.к. - непрерывна, то , т.е. при имеем . Поэтом (т.к. - непрерывна) имеем: .

16.На листочке с вопросами на обороте

17.Непрерывность сложной функции. Обратная функция и ее непрерывность/

Теорема о непрерывности сложной функции.

Пусть функция (t) непрерывна в точке t₀ и функция f(x) непрерывна в точке х₀=(t₀). Тогда функция f((t)) непрерывна в точке t₀.

Доказательство.

Для доказательства этой теоремы воспользуемся формальным преобразованием двух строчек кванторов. Имеем

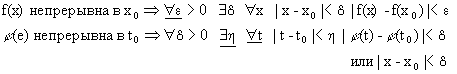
Выписывая подчеркнутые кванторы, получим, что

,

что и говорит о том, что f((t)) непрерывна в точке t₀. 

Обратите внимание на следующие детали:

а) т.к. x=(t), то |(t)-(t₀)|< может быть записано как |x-x₀|<, и f(x) превращается в F((t));

б) при определении непрерывности (t) в точке t₀ в первом кванторе стоит буква . Это необходимо для согласования с квантором в предыдущей строке и взаимного уничтожения . Любая другая буква на этом месте не дала бы верного результата.

Определение.Пусть имеется функция f(x) определенная на отрезке <a,b>, значения которой принадлежат некоторому отрезку <c,d>. Если

,

то говорят, что на отрезке <c,d> определена функция, обратная к функции f(x) и обозначают это так:x=f^(-1)(y).

Обратите внимание на отличие этого определения от определения заполненности отрезка <c,d> сплошь. В определении f^(-1)(…) стоит квантор , т.е. значение х, обеспечивающее равенство y=f(x), должно быть единственным, в то время как в определении заполненности отрезка<c,d> сплошь стоит квантор , что говорит о том, что может быть несколько значений х, удовлетворяющих равенству y=f(x).

Обычно, говоря об обратной функции, заменяют х на у а y на x(xy) и пишут y=f^(-1)(x). Очевидно, что исходная функция f(x) и обратная функция f^(-1)(x) удовлетворяют соотношению

f^(-1)(f(x))=f(f^(-1)(x))=x.

Графики исходной и обратной функции получаются друг из друга зеркальным отображением относительно биссектрисы первого квадранта.

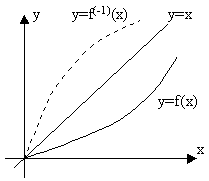
Теорема. Пусть функция f(x) определена, непрерывна и строго монотонно возрастает (убывает) на отрезке [a,b]. Тогда на отрезке [f(a),f(b)] определена обратная функция f^(-1)(x), которая также непрерывна и строго монотонно возрастает (убывает).

Доказательство.

Докажем теорему для случая, когда f(x) строго монотонно возрастает.

1. Существование обратной функции.

Так как по условию теоремы f(x) непрерывна, то, согласно предыдущей теореме, отрезок [f(a),f(b)] заполнен сплошь. Это означает, что .

Докажем, что х единственно. Действительно, если взять х’>x, то будет f(x’)>f(x)=y и поэтому f(x’)>y. Если взять х’’<x, то будет f(x’’)<f(x)=y и поэтому f(x’’)<y. В обоих случаях f(x) y и поэтому x единственно. Следовательно, х=f^(-1)(y) и f^(-1)(…) существует.

2. Монотонность обратной функции.

Сделаем обычную замены xy и будем писать y= f^(-1)(x). Это значит, что x=f(y).

Пусть x₁>x₂. Тогда:

y₁= f^(-1)(x₁); x₁=f(y₁)

y₂= f^(-1)(x₂); x₂=f(y₂)

Какое же соотношение между y₁ и y₂? Проверим возможные варианты.

а) y₁<y₂? Но тогда f(y₁)<f(y₂) и x₁<x₂, а у нас было x₁>x₂.

б) y₁=y₂? Но тогда f(y₁)=f(y₂) и x₁=x₂, а у нас было x₁>x₂.

в) Остается единственный вариант y₁>y₂, т.е. Но тогда f^(-1)(x₁)>f^(-1)(x₂), а это и означает, что f^(-1)(…) строго монотонно возрастает.

3. Непрерывность обратной функции.

Т.к. значения обратной функции заполняют сплошь отрезок [a,b], то по предыдущей теоремеf^(-1)(…) непрерывна. 