
- •1.Множество r действительных чисел. Геометрическое изображение действительных чисел. Ограниченные и неограниченные множества. Промежутки. Понятие множества
- •Операции над множествами.
- •Свойства операций над множествами.
- •Геометрическое изображение действительных чисел
- •Числовые промежутки
- •2.Отображения (функции) и их свойства. (стр. 100 Письменный)Действительная функция действительного переменного. График функции. Способы задания функции. (стр. 101-102 Письменный)
- •Свойства композиции
- •Дополнительные свойства
- •Примеры
- •Свойства
- •Единственность предела.
- •7.Предел сложной функции. Предельный переход в неравенствах. Предельный переход в неравенствах
- •8. Односторонние пределы Точки разрыва и их классификация
- •Точки разрыва и их классификация
- •9. Бесконечно малые величины и их сравнение
- •Сравнение бесконечно малых [править] Определения
- •[Править] Примеры сравнения
- •10. Бесконечно большие величины
- •11. Пределы рациональных выражений.
- •13.Принцип вложенных отрезков. Предел монотонной переменной.
- •Предел монотонной последовательности
- •Часть 1. Пусть ограниченны сверху, т.Е. Такое, что . Тогда, согласно теореме о существовании супремума мы можем утверждать, что .
- •Часть 2. Пусть теперь неограниченна сверху. Это значит, что .
- •Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики. Способы определения
- •15.Непрерывность функции в точке. Непрерывность суммы, произведения и частного.
- •16.На листочке с вопросами на обороте
- •17.Непрерывность сложной функции. Обратная функция и ее непрерывность/
- •Непрерывность обратной функции
- •19. Показательная функция и ее алгебраические свойства Пусть — неотрицательное вещественное число, — рациональное число: . Тогда определяется по следующим правилам.
- •20. Существование логарифмов.Логарифмическая функция и ее алгебраические свойства.
- •Основные характеристики
- •Замена основания логарифма
- •Другие тождества и свойства
- •22. Обратные тригонометрические функции
- •23. Дифференцируемость и производная. Скорость.
- •Производная
- •Скорость изменения функции
- •25. Правила вычисления производных
- •Производные элементарных функций
- •Производная суммы и разности
- •Производная произведения
- •Производная частного
- •Производная сложной функции
- •Правила дифференцирования
- •26. Производная степенной, показательной и логарифмической функции.
- •Производная показательной функции.
- •Производная логарифмической функции.
- •27.Дифференцирование обратной функции. Дифференцирование сложной функции.
- •Дифференцирование сложной и обратной функций
- •28. Производные высших порядков. Механический смысл второй производной.
- •29 Параметрическое задание функции. Дифференцирование функции заданной параметрическим способом.
- •Дифференцирование функции, заданной параметрически
- •30. Дифференциал и его связь с производной. Геометрический и механический смысл дифференциала.
- •, То либо минимум, либо максимум, либо они оба
- •Достигаются во внутренней точке по теореме Ферма
- •36. Теорема Коши. Раскрытие неопределенностей.
- •39. Нахождение наибольшего и наименьшего значений функций непрерывной на отрезке непрерывной на отрезке
- •Алгоритм
- •Нахождение наибольшего и наименьшего значений функции непрерывной на интервале
- •Теорема
- •40. Выпуклость функции и точки перегиба
- •41. Асимптоты
- •42. Общий план исследования функции и построения графика.
- •1) Отыскивается область определения функции.
- •3) Находим точки пересечения графика функции с осями координат.
- •5) Ищутся асимптоты графика функции.
- •6) Находятся критические точки и интервалы монотонности.
- •7) Ищутся точки перегиба и интервалы выпуклости.
8. Односторонние пределы Точки разрыва и их классификация
Если и при этом , то говорят, что x стремится к слева, и записывают: . Предел называют левым пределом функции .
Если и при этом , то говорят, что x стремится к справа, и записывают: . Предел называют правым пределом функции .
Левый и правый пределы функции называются односторонними пределами. Для существования предела функции при x, стремящемся к , необходимо и достаточно, чтобы .
Точки разрыва и их классификация
Если в какой-либо точке функция не определена, либо и (или) , то точка называется точкой разрыва функции, а сама функция - разрывной в этой точке.
Если - точка разрыва функции , и существуют конечные пределы и , то точка называется точкой разрыва первого рода.
Точки разрыва первого рода делятся на:
точки устранимого разрыва, если ;
точки скачка, если ;
Если хотя бы один из односторонних пределов не является конечным, то точка есть точка разрыва второго рода.
9. Бесконечно малые величины и их сравнение
Последовательность
![]() называется
бесконечно малой, если
называется
бесконечно малой, если
![]() .
Например, последовательность чисел
.
Например, последовательность чисел
![]() —
бесконечно малая.
—
бесконечно малая.
Функция
называется бесконечно малой в
окрестности точки
![]() ,
если
,
если
![]() .
.
Функция
называется бесконечно малой на
бесконечности, если
![]() либо
либо
![]() .
.
Также
бесконечно малой является функция,
представляющая собой разность функции
и её предела, то есть если
![]() ,
то
,
то
![]() ,
,
![]() .
.
Сравнение бесконечно малых [править] Определения
Допустим,
у нас есть бесконечно малые при одном
и том же
![]() величины
величины
![]() и
и
![]() (либо,
что не важно для определения, бесконечно
малые последовательности).
(либо,
что не важно для определения, бесконечно
малые последовательности).
Если
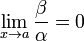 ,
то
,
то
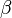 —
бесконечно малая высшего
порядка малости,
чем
—
бесконечно малая высшего
порядка малости,
чем
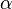 .
Обозначают
.
Обозначают
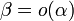 или
β≺α.
или
β≺α.Если
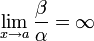 ,
то
—
бесконечно малая низшего
порядка малости,
чем
.
Соответственно
,
то
—
бесконечно малая низшего
порядка малости,
чем
.
Соответственно
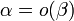 или
α≺β.
или
α≺β.Если
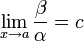 (предел
конечен и не равен 0), то
и
являются
бесконечно малыми величинами одного
порядка малости.
Это обозначается как α≍β
или как одновременное выполнение
отношений
(предел
конечен и не равен 0), то
и
являются
бесконечно малыми величинами одного
порядка малости.
Это обозначается как α≍β
или как одновременное выполнение
отношений
 и
и
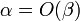 .
Следует заметить, что в некоторых
источниках можно встретить обозначение,
когда одинаковость порядков записывают
в виде только одного отношения «о
большое», что является вольным
использованием данного символа.
.
Следует заметить, что в некоторых
источниках можно встретить обозначение,
когда одинаковость порядков записывают
в виде только одного отношения «о
большое», что является вольным
использованием данного символа.Если
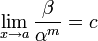 (предел
конечен и не равен 0), то бесконечно
малая величина
имеет
(предел
конечен и не равен 0), то бесконечно
малая величина
имеет
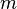 -й
порядок малости
относительно бесконечно малой
.
-й
порядок малости
относительно бесконечно малой
.
Для вычисления подобных пределов удобно использовать правило Лопиталя.
[Править] Примеры сравнения
При
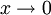 величина
величина
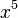 имеет
высший порядок малости относительно
имеет
высший порядок малости относительно
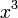 ,
так как
,
так как
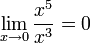 .
С другой стороны,
имеет
низший порядок малости относительно
,
так как
.
С другой стороны,
имеет
низший порядок малости относительно
,
так как
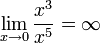 .
.
С
использованием О-символики
полученные результаты могут быть
записаны в следующем виде
![]() .
.
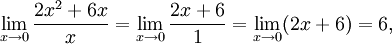 то
есть при
то
есть при
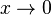 функции
функции
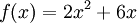 и
и
 являются
бесконечно малыми величинами одного
порядка.
являются
бесконечно малыми величинами одного
порядка.
В
данном случае справедливы записи
![]() и
и
![]()
При бесконечно малая величина
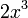 имеет
третий порядок малости относительно
имеет
третий порядок малости относительно
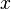 ,
поскольку
,
поскольку
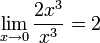 ,
бесконечно малая
,
бесконечно малая
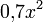 —
второй порядок, бесконечно малая
—
второй порядок, бесконечно малая
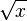 —
порядок 0,5.
—
порядок 0,5.
10. Бесконечно большие величины
Во
всех приведённых ниже формулах
бесконечность справа от равенства
подразумевается определённого знака
(либо «плюс», либо «минус»). То есть,
например, функция
![]() ,
неограниченная с обеих сторон, не
является бесконечно большой при
,
неограниченная с обеих сторон, не
является бесконечно большой при
![]() .
.
Последовательность
называется
бесконечно большой, если
![]() .
.
Функция
называется бесконечно большой в
окрестности точки
,
если
![]() .
.
Функция
называется бесконечно большой на
бесконечности, если
![]() либо
либо
![]() .
.
