
- •1.Множество r действительных чисел. Геометрическое изображение действительных чисел. Ограниченные и неограниченные множества. Промежутки. Понятие множества
- •Операции над множествами.
- •Свойства операций над множествами.
- •Геометрическое изображение действительных чисел
- •Числовые промежутки
- •2.Отображения (функции) и их свойства. (стр. 100 Письменный)Действительная функция действительного переменного. График функции. Способы задания функции. (стр. 101-102 Письменный)
- •Свойства композиции
- •Дополнительные свойства
- •Примеры
- •Свойства
- •Единственность предела.
- •7.Предел сложной функции. Предельный переход в неравенствах. Предельный переход в неравенствах
- •8. Односторонние пределы Точки разрыва и их классификация
- •Точки разрыва и их классификация
- •9. Бесконечно малые величины и их сравнение
- •Сравнение бесконечно малых [править] Определения
- •[Править] Примеры сравнения
- •10. Бесконечно большие величины
- •11. Пределы рациональных выражений.
- •13.Принцип вложенных отрезков. Предел монотонной переменной.
- •Предел монотонной последовательности
- •Часть 1. Пусть ограниченны сверху, т.Е. Такое, что . Тогда, согласно теореме о существовании супремума мы можем утверждать, что .
- •Часть 2. Пусть теперь неограниченна сверху. Это значит, что .
- •Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики. Способы определения
- •15.Непрерывность функции в точке. Непрерывность суммы, произведения и частного.
- •16.На листочке с вопросами на обороте
- •17.Непрерывность сложной функции. Обратная функция и ее непрерывность/
- •Непрерывность обратной функции
- •19. Показательная функция и ее алгебраические свойства Пусть — неотрицательное вещественное число, — рациональное число: . Тогда определяется по следующим правилам.
- •20. Существование логарифмов.Логарифмическая функция и ее алгебраические свойства.
- •Основные характеристики
- •Замена основания логарифма
- •Другие тождества и свойства
- •22. Обратные тригонометрические функции
- •23. Дифференцируемость и производная. Скорость.
- •Производная
- •Скорость изменения функции
- •25. Правила вычисления производных
- •Производные элементарных функций
- •Производная суммы и разности
- •Производная произведения
- •Производная частного
- •Производная сложной функции
- •Правила дифференцирования
- •26. Производная степенной, показательной и логарифмической функции.
- •Производная показательной функции.
- •Производная логарифмической функции.
- •27.Дифференцирование обратной функции. Дифференцирование сложной функции.
- •Дифференцирование сложной и обратной функций
- •28. Производные высших порядков. Механический смысл второй производной.
- •29 Параметрическое задание функции. Дифференцирование функции заданной параметрическим способом.
- •Дифференцирование функции, заданной параметрически
- •30. Дифференциал и его связь с производной. Геометрический и механический смысл дифференциала.
- •, То либо минимум, либо максимум, либо они оба
- •Достигаются во внутренней точке по теореме Ферма
- •36. Теорема Коши. Раскрытие неопределенностей.
- •39. Нахождение наибольшего и наименьшего значений функций непрерывной на отрезке непрерывной на отрезке
- •Алгоритм
- •Нахождение наибольшего и наименьшего значений функции непрерывной на интервале
- •Теорема
- •40. Выпуклость функции и точки перегиба
- •41. Асимптоты
- •42. Общий план исследования функции и построения графика.
- •1) Отыскивается область определения функции.
- •3) Находим точки пересечения графика функции с осями координат.
- •5) Ищутся асимптоты графика функции.
- •6) Находятся критические точки и интервалы монотонности.
- •7) Ищутся точки перегиба и интервалы выпуклости.
Числовые промежутки
Решение неравенств обозначают на координатной прямой.
Пусть a - некоторое число. Часть координатной прямой левее точки a вместе с точкой a (черный (закрашенный) кружок)
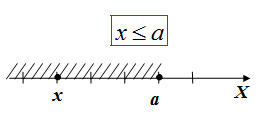
Часть координатной прямой левее точки a, но не включая точку
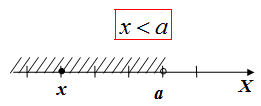
Аналогично, если x находится правее
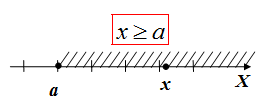
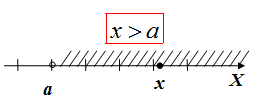
Обозначения числовых множеств на координатной прямой носят название: числовые промежутки.

2.Отображения (функции) и их свойства. (стр. 100 Письменный)Действительная функция действительного переменного. График функции. Способы задания функции. (стр. 101-102 Письменный)
3.Арифметические действия над функциями. Композиции функций.
Пусть
![]() и
и
![]() две
функции. Тогда их композицией называется
функция
две
функции. Тогда их композицией называется
функция
![]() ,
определённая равенством:
,
определённая равенством:
![]() .
.
Связанные определения
Термин «сложная функция» может быть применим к композиции двух функций, тем не менее он чаще употребляется в ситуации когда на вход функции нескольких переменных подаётся набор функций от одной или нескольких исходных переменных. Например функция
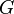 вида
вида
![]()
Свойства композиции
Композиция ассоциативна:
![]() .
.
Если
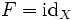 —
тождественное
отображение на
—
тождественное
отображение на
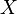 ,
то есть
,
то есть
![]() ,
,
то
![]() .
.
Если
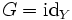 —
тождественное отображение на
—
тождественное отображение на
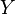 ,
то есть
,
то есть
![]() ,
,
то
![]() .
.
Рассмотрим пространство всех биекций множества на себя и обозначим его
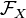 .
То есть если
.
То есть если
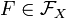 ,
то
,
то
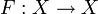 —
биекция. Тогда композиция функций из
является
бинарной
операцией, а
—
биекция. Тогда композиция функций из
является
бинарной
операцией, а
 —
группой.
—
группой.
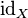 является
нейтральным
элементом этой
группы. Обратным
к элементу
является
является
нейтральным
элементом этой
группы. Обратным
к элементу
является
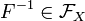 —
обратная
функция.
—
обратная
функция.Группа , вообще говоря, не коммутативна, то есть
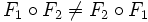 .
.
Дополнительные свойства
Композиция непрерывных функций непрерывна. Пусть
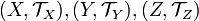 —
топологические
пространства.
Пусть
—
топологические
пространства.
Пусть
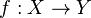 и
и
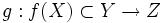 две
функции,
две
функции,
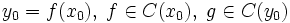 .
Тогда
.
Тогда
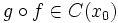 .
.
Композиция дифференцируемых функций дифференцируема. Пусть
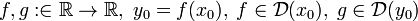 .
Тогда
.
Тогда
 ,
и
,
и
![]()
4.Числовые последовательности. Подпоследовательности. Окрестности точек .
Пусть
множество
—
это либо множество вещественных чисел
![]() ,
либо множество комплексных чисел
,
либо множество комплексных чисел
![]() .
Тогда последовательность
.
Тогда последовательность
![]() элементов
множества
называется
числовой последовательностью..
Подпоследовательность
последовательности
элементов
множества
называется
числовой последовательностью..
Подпоследовательность
последовательности
![]() —
это последовательность
—
это последовательность
![]() ,
где
,
где
![]() —
возрастающая последовательность
элементов множества натуральных чисел.
—
возрастающая последовательность
элементов множества натуральных чисел.
Иными словами, подпоследовательность получается из последовательности удалением конечного или счётного числа элементов.
Примеры
Последовательность простых чисел является подпоследовательностью последовательности натуральных чисел.
Последовательность натуральных чисел, кратных 12, является подпоследовательностью последовательности чётных натуральных чисел.
Свойства
Всякая последовательность является своей подпоследовательностью.
Для всякой подпоследовательности
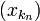 верно,
что
верно,
что
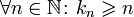 .
.
Подпоследовательность сходящейся последовательности сходится к тому же пределу, что и исходная последовательность.
Если все подпоследовательности некоторой исходной последовательности сходятся, то их пределы равны.
Любая подпоследовательность бесконечно большой последовательности также является бесконечно большой.
Из любой неограниченной числовой последовательности можно выделить бесконечно большую подпоследовательность, все элементы которой имеют определённый знак.
Из любой числовой последовательности можно выделить либо сходящуюся подпоследовательность, либо бесконечно большую подпоследовательность, все элементы которой имеют определённый знак.
Окрестности
точек. Окрестность точки. 1.
На числовой оси окрестность точки
– любой интервал (открытый промежуток),
содержащий данную точку. В частности
открытый (не содержащий границ) промежуток
(а – δ; а + δ) с центром в точке
а называется δ-окрестностью
точки а (положительное число δ –
радиус δ-окрестности).
2. В n-мерном
пространстве окрестность точки – любая
область,
содержащая данную точку. В частности
совокупность точек М(х1;
х2; …; хn),
координаты которых удовлетворяют
неравенству
![]() ,
называется
шаровой (сферической) δ-окрестностью
точки А(а1; а2;
…; аn) – окрестностью
радиуса δ. Иначе говоря, указанное
множество точек М образует в
n-мерном пространстве (открытый)
шар радиуса δ с центром в точке А.
Множество точек М(х1;
х2; …; хn),
координаты которых удовлетворяют
системе неравенств
,
называется
шаровой (сферической) δ-окрестностью
точки А(а1; а2;
…; аn) – окрестностью
радиуса δ. Иначе говоря, указанное
множество точек М образует в
n-мерном пространстве (открытый)
шар радиуса δ с центром в точке А.
Множество точек М(х1;
х2; …; хn),
координаты которых удовлетворяют
системе неравенств
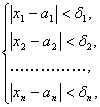 называется
параллелепипедальной окрестностью
точки А(а1; а2; …; аn).
Иначе: указанное множество точек М
образует в n-мерном пространстве
параллелепипед с центром в точке А.
3.
Окрестность точки А в метрическом
пространстве –
любая область, содержащая точку А.
В частности все точки М, расстояние
от которых до точки А меньше
некоторого положительного числа δ,
образуют ее (т.е. точки А) сферическую
окрестность радиуса δ с центром в точке
А.
называется
параллелепипедальной окрестностью
точки А(а1; а2; …; аn).
Иначе: указанное множество точек М
образует в n-мерном пространстве
параллелепипед с центром в точке А.
3.
Окрестность точки А в метрическом
пространстве –
любая область, содержащая точку А.
В частности все точки М, расстояние
от которых до точки А меньше
некоторого положительного числа δ,
образуют ее (т.е. точки А) сферическую
окрестность радиуса δ с центром в точке
А.
Предельные
точки множества. ПРЕДЕЛЬНАЯ
ТОЧКАмножества-
точка, в любой окрестности к-рой содержится
по крайней мере одна точка данного
множества, отличная от нее самой.
Рассматриваемые множества и точка
предполагаются принадлежащими нек-рому
топологич. пространству. Множество,
содержащее все свои П. т., наз. замкнутым.
Совокупность всех П. т. множества Мназ.
производным множеством и обозначается
М'.
Если рассматриваемое топологич.
пространство X
удовлетворяет
первой аксиоме отделимости (для любых
двух его точек х
и
усуществует окрестность U(х),
не содержащая точку у),
то
каждая окрестность П. т. нек-рого множества
![]() содержит
бесконечно много точек этого множества
и производное множество М'
-
замкнуто. Всякая прикосновения
точка
множества Мявляется либо его П. т., либо
изолированной.
содержит
бесконечно много точек этого множества
и производное множество М'
-
замкнуто. Всякая прикосновения
точка
множества Мявляется либо его П. т., либо
изолированной.
5.Понятие предела последовательности и функции. Постоянное число а называется пределомпоследовательности {x n }, если для любого сколь угодно малого положительного числа существует номер N, что все значения x n,у которых n>N, удовлетворяют неравенству
x n- a < . (6.1)
Записывают
это следующим образом:
![]() или
x na.
или
x na.
Неравенство (6.1) равносильно двойному неравенству
a- < x n < a + , (6.2)
которое означает, что точки x n, начиная с некоторого номера n>N, лежат внутри интервала (a- , a+ ), т.е. попадают в какую угодно малую -окрестность точки а.
Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся.
Понятие предела функции является обобщением понятия предела последовательности, так как предел последовательности можно рассматривать как предел функции x n = f(n) целочисленного аргумента n.
Пусть дана функция f(x) и пусть a- предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a. Точка aможет принадлежать множеству D(f), а может и не принадлежать ему.
Определение 1. Постоянное число А называется пределомфункцииf(x) при x a, если для всякой последовательности {x n } значений аргумента, стремящейся к а, соответствующие им последовательности {f(x n )} имеют один и тот же предел А.
Это определение называют определением предела функции по Гейне,или “ на языке последовательностей”.
Определение 2 . Постоянное число А называется пределомфункцииf(x) приx a, если, задав произвольное как угодно малое положительное число , можно найти такое >0 (зависящее от ), что для всех x, лежащих в -окрестности числа а, т.е. для x, удовлетворяющих неравенству 0 < x-a < , значения функции f(x) будут лежать в -окрестности числа А, т.е. f(x)-A < .
Это определение называют определением предела функции по Коши, или “на языке - “.
Определения 1 и 2 равносильны. Если функция f(x) при x a имеет предел, равный А, это записывается в виде
![]() .
(6.3)
.
(6.3)
В том случае, если последовательность {f(x n )} неограниченно возрастает (или убывает) при любом способе приближения xк своему пределу а, то будем говорить, что функция f(x) имеет бесконечный предел,и записывать это в виде:
![]()
Переменная величина (т.е. последовательность или функция), имеющая своим пределом нуль, называется бесконечно малой величиной.
Переменная величина, имеющая бесконечный предел, называется бесконечно большой величиной.
