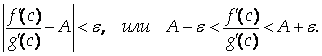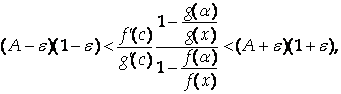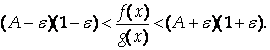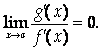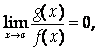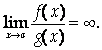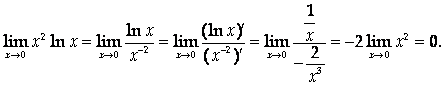- •1.Множество r действительных чисел. Геометрическое изображение действительных чисел. Ограниченные и неограниченные множества. Промежутки. Понятие множества
- •Операции над множествами.
- •Свойства операций над множествами.
- •Геометрическое изображение действительных чисел
- •Числовые промежутки
- •2.Отображения (функции) и их свойства. (стр. 100 Письменный)Действительная функция действительного переменного. График функции. Способы задания функции. (стр. 101-102 Письменный)
- •Свойства композиции
- •Дополнительные свойства
- •Примеры
- •Свойства
- •Единственность предела.
- •7.Предел сложной функции. Предельный переход в неравенствах. Предельный переход в неравенствах
- •8. Односторонние пределы Точки разрыва и их классификация
- •Точки разрыва и их классификация
- •9. Бесконечно малые величины и их сравнение
- •Сравнение бесконечно малых [править] Определения
- •[Править] Примеры сравнения
- •10. Бесконечно большие величины
- •11. Пределы рациональных выражений.
- •13.Принцип вложенных отрезков. Предел монотонной переменной.
- •Предел монотонной последовательности
- •Часть 1. Пусть ограниченны сверху, т.Е. Такое, что . Тогда, согласно теореме о существовании супремума мы можем утверждать, что .
- •Часть 2. Пусть теперь неограниченна сверху. Это значит, что .
- •Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики. Способы определения
- •15.Непрерывность функции в точке. Непрерывность суммы, произведения и частного.
- •16.На листочке с вопросами на обороте
- •17.Непрерывность сложной функции. Обратная функция и ее непрерывность/
- •Непрерывность обратной функции
- •19. Показательная функция и ее алгебраические свойства Пусть — неотрицательное вещественное число, — рациональное число: . Тогда определяется по следующим правилам.
- •20. Существование логарифмов.Логарифмическая функция и ее алгебраические свойства.
- •Основные характеристики
- •Замена основания логарифма
- •Другие тождества и свойства
- •22. Обратные тригонометрические функции
- •23. Дифференцируемость и производная. Скорость.
- •Производная
- •Скорость изменения функции
- •25. Правила вычисления производных
- •Производные элементарных функций
- •Производная суммы и разности
- •Производная произведения
- •Производная частного
- •Производная сложной функции
- •Правила дифференцирования
- •26. Производная степенной, показательной и логарифмической функции.
- •Производная показательной функции.
- •Производная логарифмической функции.
- •27.Дифференцирование обратной функции. Дифференцирование сложной функции.
- •Дифференцирование сложной и обратной функций
- •28. Производные высших порядков. Механический смысл второй производной.
- •29 Параметрическое задание функции. Дифференцирование функции заданной параметрическим способом.
- •Дифференцирование функции, заданной параметрически
- •30. Дифференциал и его связь с производной. Геометрический и механический смысл дифференциала.
- •, То либо минимум, либо максимум, либо они оба
- •Достигаются во внутренней точке по теореме Ферма
- •36. Теорема Коши. Раскрытие неопределенностей.
- •39. Нахождение наибольшего и наименьшего значений функций непрерывной на отрезке непрерывной на отрезке
- •Алгоритм
- •Нахождение наибольшего и наименьшего значений функции непрерывной на интервале
- •Теорема
- •40. Выпуклость функции и точки перегиба
- •41. Асимптоты
- •42. Общий план исследования функции и построения графика.
- •1) Отыскивается область определения функции.
- •3) Находим точки пересечения графика функции с осями координат.
- •5) Ищутся асимптоты графика функции.
- •6) Находятся критические точки и интервалы монотонности.
- •7) Ищутся точки перегиба и интервалы выпуклости.
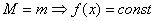
, То либо минимум, либо максимум, либо они оба
Достигаются во внутренней точке по теореме Ферма
ч.т.д.
Теорема Лагранжа:
Пусть - гладкая функция
на отрезке , тогда
такая,
что
![]() .
.
|
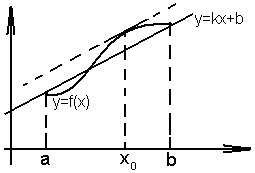
Можно задать вопрос: “А есть ли прямая, параллельная этой хорде?”
Есть,
конечно!
Производная – угловой
коэффициент касательной
|
Доказательство:
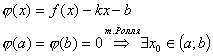 такая,
что
такая,
что
![]() ч.т.д.
ч.т.д.
Следствие теоремы Ролля:
Если
![]() ,
то
монотонно возрастает.
Доказательство:
пусть
,
то
монотонно возрастает.
Доказательство:
пусть
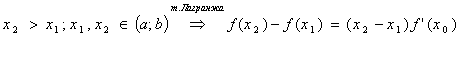 ,
где
,
где
![]() .
.
![]() монотонно возрастает.
Обратное
утверждение к теореме
монотонно возрастает.
Обратное
утверждение к теореме
Ферма
неверно, т.к. может быть перегиб.
Пример:
![]()
35.Применение теоремы Лагранжа к исследованию функции на монотонность.
36. Теорема Коши. Раскрытие неопределенностей.
Теорема.Если f, g непрерывны на [a,b], дифференцируемы на (a,b), то существует
xО(a,b): gў(x) (f (b) - f (a)) = fў(x) (g (b) - g (a)).
Доказательство.Рассмотрим вспомогательную функцию
F (x) = g (x) (f (b)- f (a)) - f (x) (g (b) - g (a)).
Для этой функции
F (a) = g (a) (f (b) - f (a)) - f (a) (g (b) - g (a)) = g (a) f (b) - f (a) g (b),
F (b) = g (b) (f (b) - f (a)) - f (b) (g (b) - g (a)) = - f (a) g (b) +g (a) f (b),
таким образом, F (a) =F (b) и к ней применима теорема Ролля:существует точка xО(a,b) для которой выполняется равенство
0=F (b) - F (a) =Fў(x) (b-a) = [gў(x) (f (b) - f (a)) - fў(x) (g (b) - g (a))] (b-a).
Следствие.Если gў(x) №0на (a,b), то
![]() .
.
Доказательство.Если gў(x) №0,то g (b) - g (a) №0.Иначе, в случаеg (b) =g (a), по теореме Ролля нашлась бы точка x,где gў(x) =0.
Теорема Коши
Рассмотрим,наконец, третью теорему о среднем,принадлежащей Коши (1789–1859), которая является обобщением теоремы Лагранжа.
Теорема.Если
функции![]() и
и
![]() непрерывны
на отрезке
непрерывны
на отрезке
![]() и
дифференцируемы во всех его внутренних
точках, причем
и
дифференцируемы во всех его внутренних
точках, причем![]() не
обращается в ноль ни в одной из указанных
точек, то существует,по крайней мере,
одна точка
не
обращается в ноль ни в одной из указанных
точек, то существует,по крайней мере,
одна точка![]() ,в
которой
,в
которой
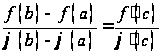 .
.
Доказательство.Так
как
![]() во
всех точках
во
всех точках![]() ,то
отсюда следует,что
,то
отсюда следует,что
![]() .В
противном случае, как следует из теоремы
Ролля,существовала хотя бы одна точка
,в
которой
.В
противном случае, как следует из теоремы
Ролля,существовала хотя бы одна точка
,в
которой
![]() .
.
Составим вспомогательную функцию
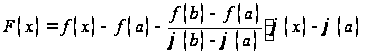 .
.
Данная
функция непрерывна на отрезке
и
дифференцируема во всех его внутренних
точках. Кроме того, вычисление ее в
точках
![]() и
и
![]() дает:
дает:
![]() .Значит,
функция
.Значит,
функция![]() удовлетворяет
требованиям теоремы Ролля,то есть
существует хотя бы одна точка
,в
которой
удовлетворяет
требованиям теоремы Ролля,то есть
существует хотя бы одна точка
,в
которой
![]() .
.
Вычислим производную :
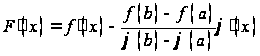 .
.
Из условия следует, что
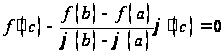 и
,
и
,
что и требовалось доказать.
В
случае,когда
![]() ,теорема
Коши переходит в формулировку теоремы
Лагранжа.
,теорема
Коши переходит в формулировку теоремы
Лагранжа.
Раскрытие неопределенностей |
|
|
|
Если
функции F(X)
И
G(X)
удовлетворяют на некотором отрезке
[Ab]
условиям теоремы Коши и F(A)
= G(A) = 0,
то отношение F(X)/G(X)
Не
определено при Х=а,
но определено при остальных значениях
Х.
Поэтому можно поставить задачу
вычисления предела этого отношения
при
Теорема 3 (правило Лопиталя). Пусть функции F(X) и G(X) Удовлетворяют на отрезке [Ab] условиям теоремы Коши и F(A)=G(A)=0. Тогда, если существует
То существует и
Причем
Доказательство. Выберем
Из теоремы Коши следует, что
По условию теоремы F(A)=G(A)=0, поэтому
При
То существует и
Поэтому
Теорема доказана. Пример. При A > 0
Замечание 1. Если F(X) Или G(X) Не определены при Х=а, можно доопределить их в этой точке значениями F(A)=G(A)=0. Тогда обе функции будут непрерывными в точке А, и к этому случаю можно применить теорему 3.
Замечание
2.
Если F’(A)=G’(A)=0
и F’(X)
И
G’(X)
Удовлетворяют
условиям, наложенным в теореме 3 на
F(X)
И
G(X),
к отношению
И так далее. Пример.
Правило
Лопиталя можно применять и для раскрытия
неопределенностей вида
Теорема
4.
Пусть функции F(X)
и G(X)
непрерывны и дифференцируемы при
И существует
То существует и
Причем
Доказательство. Выберем в рассматриваемой окрестности точки А Точки A и Х Так, чтобы A < X < A (или A < X < A). Тогда по теореме Коши существует точка С (A < C < X) такая, что
Так как
Получаем:
Так как
Можно для любого малого E выбрать A настолько близким к А, что для любого С будет выполняться неравенство
Для этого же значения ε из условия теоремы следует, что
Поэтому
Перемножим два полученных неравенства:
Или
Поскольку E – произвольно малое число, отсюда следует, что
Что и требовалось доказать.
Замечание
1.
Теорема 4 верна и при А=
Тогда и
Следовательно,
Замечание
2.
Теоремы 3 и 4 можно доказать и для
случая, когда
Пример.
|
37.
38.

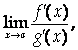
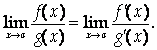
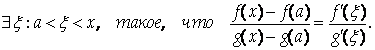
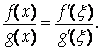
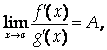
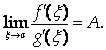
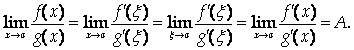
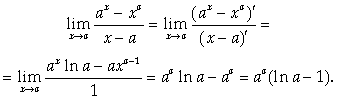

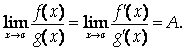
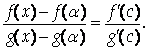
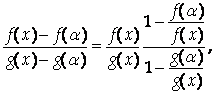
 .
.