Производная показательной функции.

Теорема 1. Функция е^х дифференцируема в каждой точке области определения, и

(е^х)' = е^х.

Доказательство. Найдем сначала приращение функции у = е^х в точке x₀:

Δy = e ^x₀^+Δx — е ^x₀ = е ^x₀ • е ^Δx — е ^x₀ = е ^x₀ (е^{Δ x} — 1).

Пользуясь условием (1), находим:

при Δx → 0

По определению производной отсюда следует, что у' = e^x т. е. (е^x)’= е^х при любом х. Число е положительно и отлично от 1, поэтому определены логарифмы по основанию е. Определение. Натуральным логарифмом (обозначается ln) называется логарифм по основанию е:

ln x = log_e х.

(2) По основному логарифмическому тождеству для любого положительного числа е^{ln a} =а. Поэтому а^х может быть записано в виде

a^x = (e^{ln a})^x = e^{x ln a}. (3)

Выведем формулу производной показательной функции при произвольном значении а. Теорема 2. Показательная функция а^х дифференцируема в каждой точке области определения, и

(а^x)'=а^хlп а.

(4) Доказательство. Из формулы (3) по теореме о производной сложной функции получаем, что показательная функция дифференцируема в каждой точке и

(a^x)’= (e^{x ln a})’= e^{x ln a}ln a = a^x ln a (5)

Следствие. Показательная функция непрерывна в каждой точке своей области определения, т. е. а^x →а^x₀ при х →х₀.

Производная логарифмической функции.

Покажем сначала, что логарифмическая функция дифференцируема в каждой точке. Графики функций y=log_ax и у = а^x симметричны относительно прямой у=х. Так как показательная функция дифференцируема в любой точке, а ее производная не обращается в нуль, график показательной функции имеет негоризонтальную касательную в каждой точке. Поэтому и график логарифмической функции имеет невертикальную касательную в любой точке. А это равносильно дифференцируемости логарифмической функции на ее области определения. Докажем теперь, что производная логарифмической функции для любого х из области определения находится по формуле

(1)

По основному логарифмическому тождеству х = е^{ln х} при всех положительных х, т. е. в этом равенстве справа и слева стоит одна и та же функция (определенная на R₊). Поэтому производные х и е^{ln x} равны, т. е.

x' = (e^{ln x})' (2)

Известно, что х' = 1. Производную правой части вычисляем по правилу нахождения производной сложной функции и теореме 1 : (е^{ln x})'= е^{ln х} ln' x=x ln' x. Подставляя найденные производные в равенство (2), находим l = х ln' х, откуда . Формула (1) показывает, что для функции на промежутке(0; ∞) любая первообразная может быть записана в виде ln x + С. Функция имеет первообразную и на промежутке (—∞; 0), это функция ln( —x). Действительно, Так как |x| = х при х>0 и |x| = —х при х<0, мы доказали, что на любом промежутке, не содержащем точку 0, первообразной для функции является функция ln |x| .

27.Дифференцирование обратной функции. Дифференцирование сложной функции.

Теорема. Пусть функция является обратной для функции . Если существует отличная от нуля производная функции по переменной x, то существует и производная обратной функции по переменной y. При этом Доказательство. По определению производной Согласно теореме о непрерывности дифференцируемых функциях, является непрерывной функцией и, следовательно, при ∆x → 0. Тогда что влечет за собой доказываемое утверждение. 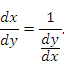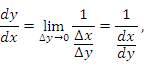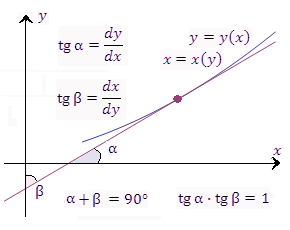Рис. 9. Геометрическая интерпретация теоремы о дифференцировании обратной функции.