ЭЛЕКТРОМАГНИТНЫЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ ПРИ НАРУШЕНИИ СИММЕТРИИ ТРЕХФАЗНОЙ ЦЕПИ

Основные положения в исследовании несимметричных переходных процессов

Общие замечания

Рассматриваемые ниже несимметричные переходные процессы ограничены условием, что несимметрия возникает только в одном каком-либо месте системы, в то время как вся остальная часть последней остается строго симметричной. Такая однократная несимметрия может быть поперечной (любой вид несимметричного короткого замыкания), и продольной (обрыв одной или двух фаз).

Строгий математический анализ несимметричных переходных процессов существенно затруднен тем дополнительным обстоятельством, что при таких процессах образуется пульсирующее магнитное поле ротора, которое в общем случае, как показано ниже, вызывает полный спектр высших гармоник. Переход от фазных переменных к переменным в координатах d, q, 0 при этом не освобождает дифференциальные уравнения от периодических коэффициентов.

Преимущества метода симметричных составляющих для исследования несимметричных режимов в симметричных трехфазных системах общеизвестны. Для стационарных условий обычно определяют лишь основные гармоники искомых величин. Именно при гаком допущении, которое принято в дальнейшем, данный метод применим также в условиях несимметричных переходных процессов.

Физические процессы при нарушении симметрии. Образование высших гармоник

На рис. 11-1 показана принципиальная модель синхронной машины, ротор которой имеет явно выраженные полюсы и не имеет демпферных контуров.

Возникновение несимметрии в цепи обмоток статора всегда приводит к возникновению наряду с симметричной системой токов прямой последовательности системы токов обратной последовательности синхронной частоты f. Каждая из указанных систем токов создают два потока, вращающихся с синхронной угловой скоростью ω во взаимно противоположных направлениях (рис. 11-1). Поток, созданный токами прямой последовательности, вращается в том же направлении, что и ротор. По отношению к последнему, очевидно он неподвижен и соответственно взаимодействует с магнитным потоком обмотки возбуждения в виде реакции размагничивающего характера. Другой поток, созданный токами обратной последовательности, вращается в противоположную сторону, по отношению к ротору и, следовательно, имеет двойную синхронную скорость 2ω по отношению к нему. Поэтому в обмотке возбуждения наведется ЭДС двойной синхронной частоты 2f. Обусловленный этой ЭДС ток частоты 2f создает пульсирующий с частотой 2f магнитный поток ротора. Разложение последнего на два потока, вращающихся в противоположные стороны с угловой скоростью 2ω относительно ротора, показывает, что один из них, вращаясь по отношению к статору с угловой скоростью (2 - ) =  в сторону, противоположную вращению ротора, оказывается неподвижным относительно потока, вызвавшего пульсирующий с частотой 2f поток ротора, и стремится его компенсировать (реакция размагничивающего характера). Что касается другого потока, то он вращается относительно статора с угловой скоростью (2 + ) = 3 в сторону вращения ротора.

Этот поток наводит в статоре ЭДС тройной синхронной частоты 3f. В результате возникает ток той же частоты, который создает пульсирующее с частотой 3f магнитное поле статора.

Продолжая подобные рассуждения, легко убедиться, что каждая нечетная гармоника однофазного переменного тока статора вызывает очередную четную гармонику тока в обмотке возбуждения, и в свою очередь каждая четная гармоника тока в обмотке возбуждения вызывает следующую по порядку нечетную гармонику тока статора. Аналогично нетрудно установить, что ток неизменного направления и четные гармоники тока статора связаны соответственно с основной и нечетными гармониками тока обмотки возбуждения. При отсутствии емкости в цепи амплитуды гармоник с ростом их порядкового номера уменьшаются.

Представим себе теперь, что в поперечной оси ротора имеется демпферная обмотка. Если воспроизводимый ею электромагнитный эффект такой же, как обмотки возбуждения, то такой ротор, очевидно, симметричен по отношению к любому перемещающемуся относительно него магнитному потоку. В рассматриваемых условиях каждая из обмоток ротора создает пульсирующий поток. Поскольку эти обмотки сдвинуты друг относительно друга в пространстве на 90° (электрических), а их потоки во времени на четверть периода, от их совместного действия образуется вращающееся круговое поле, которое по отношению к вызвавшему его магнитному потоку статора остается неподвижным и направленным навстречу. Следовательно, когда ротор симмет­ричен в обеих осях (т.е. x'_d = x'_q), неизменное или пульсирующее с произвольной частотой магнитное поле статора не создает высших гармоник.

Однако в действительности ротор синхронной машины не обладает такой симметрией, поэтому при любом несимметричном режиме синхронной машины возникают высшие гармоники, причем они проявляются при прочих равных условиях тем интенсивнее, чем больше выявлена несимметрия ротора.

Наличие демпферной обмотки только в продольной оси создает, естественно, еще большую несимметрию ротора. Напротив, при поперечной демпферной обмотке или при демпферных обмотках (с соответствующими параметрами) в обеих осях ротора достигается почти полная его симметрия (т. е. x"_d = x"_q).

Последняя обычно имеет место у турбогенераторов, в силу чего у таких машин высшие гармоники при несимметричных режимах почти не проявляются.

11-3. Применимость метода симметричных составляющих к исследованию переходных процессов

Из курса теоретических основ электротехники известно, что в электрических устройствах, выполненных симметрично, применение метода симметричных составляющих в значительной мере упрощает анализ несимметричных процессов, так как при этом симметричные составляющие токов связаны законом Ома с симметричными составляющими напряжений только одноименной последовательности. Иными словами, если какой-либо элемент цепи симметричен и обладает по отношению к симметричным составляющим токов прямой, обратной и нулевой последовательностей соответственно сопротивлениями Z₁, Z₂, Z_o, то симметричные составляющие падения напряжения в этом элементе будут:

₁ = Z_{1 1} (11-1)

₂ = Z_{2 2} (11-2)

₀ = Z_{0 0} (11-3)

Сопротивления Z₁, Z₂ и Z_o для сокращения обычно называют сопротивлениями соответственно прямой, обратной и нулевой последовательностей. Их величины для одного и того же элемента в общем случае различны.

Из изложенного, казалось бы, уже можно сделать вывод, что если временные величины в рассматриваемом процессе могут быть разложены на системы симметричных составляющих и тогда известный метод симметричных составляющих в своей обычной форме может быть применен к исследованию несимметричных переходных процессов. Однако такой вывод был бы еще преждевременным.

Дело в том, что, как показано выше, у синхронной машины с несимметричным ротором возникающее при несимметричном режиме инверсное магнитное поле статора порождает прямое магнитное поле статора, вращающееся с соответственно большей скоростью. Обращаясь к терминологии метода симметричных составляющих, можно сказать, что это равносильно тому, что магнитное поле обратной последовательности, созданное системой токов обратной последовательности какой-либо частоты, вызывает магнитное поле прямой последовательности и связанную с ними систему токов прямой последовательности, порядковые номера частот которых на два больше соответствующего номера частоты токов обратной последовательности. Другими словами, при этом оказываются взаимно связанными системы токов прямой и обратной последовательностей разных частот, что налагает дополнительные условия и требования на метод симметричных составляющих. Что касается системы токов нулевой последовательности, то создаваемое ими результирующее магнитное поле в расточке статора при любой частоте практически близко к нулю и никакой магнитной связи с ротором не создает.

Дальнейшее развитие представлений метода симметричных составляющих применительно к синхронным машинам с несимметричным ротором в условиях установившихся режимов и переходных процессов при нарушении симметрии впервые дано Н. Н. Щедриным. Помимо математического обоснования такого развития, им предложены для учета высших гармоник специальные цепные схемы, применение которых особенно эффективно при выполнении расчетов с помощью моделей или иных расчетных установок.

В подавляющем числе практических расчетов несимметричных переходных процессов обычно ограничиваются учетом лишь основной гармоники токов и напряжений. Именно только при таком допущении представляется возможным применять метод симметричных составляющих в его обычной форме, характеризуя для этого синхронную машину в схеме обратной последовательности соответствующей реактивностью х₂.

Остановимся еще на одном вопросе, в понимании которого часто встречаются трудности.

Протекающие по обмоткам статора токи прямой, обратной и нулевой последовательностей создают магнитные потоки тех же последовательностей. Последние наводят в статоре соответствующие ЭДС. Вводить эти ЭДС в расчет нецелесообразно, так как они пропорциональны (при пренебрежении насыщением магнитной системы машины) токам отдельных последовательностей, значения которых еще подлежат определению. Поэтому в дальнейшем вводим в расчет только те ЭДС, которые или известны, или не зависят от внешних условий цепи статора, причем в силу симметричного выполнения статорной обмотки эти ЭДС являются ЭДС только прямой последовательности. Что касается ЭДС, обусловленных реакцией токов отдельных последовательностей, то их учитываем в виде падений напряжений с обратным знаком в соответствующих реактивностях машины.

И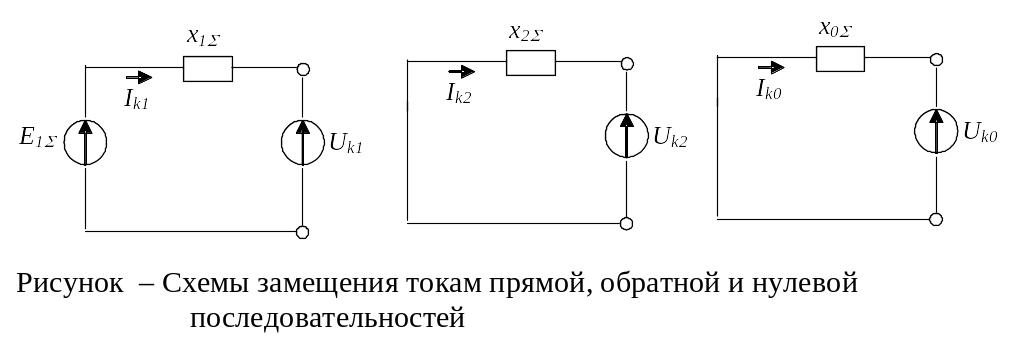 з изложенного следует, что при принятом способе учета ЭДС, обусловленных реакцией токов отдельных последовательностей, образование токов обратной и нулевой последовательностей можно представить как следствие возникающих в месте короткого замыкания напряжений обратной и нулевой последовательностей.

Таким образом задача расчета несимметричных КЗ связана с нахождением шести неизвестных: трех симметричных составляющих токов и трех составляющих напряжений.

Для их нахождения при любом виде КЗ всегда будем использовать три уравнения, соответствующие второму закону Кирхгофа.

;

;

,

где _к1, _к2, _к0, _к1,, _к2, _к0 —симметричные составляющие напряжения и тока в месте короткого замыкания;

_1 - результирующая ЭДС относительно точки короткого замыкания;

x_1, x_2, x_0 — результирующие сопротивления схем соответствующих последовательностей относительно точки короткого замыкания.

Недостающие три уравнения легко получить из граничных условий, которыми характеризуется тот или иной вид несимметричного повреждения.

Все соотношения будем записывать для особой фазы, т.е. фазы, которая находится в условиях, отличающихся от условий, в которых находятся другие фазы. В качестве особой фазы всегда будем принимать фазу А.