КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ И КИБЕРНЕТИКИ

Численные методы отчет: «Табулирование трансцендентных функций»

Выполнил:

Хабибуллин А.Р. 991э

Проверила:

КАЗАНЬ

2013

Вариант 8

Цель задания – изучить и сравнить различные способы приближенного вычисления функции ошибок:

Постановка задачи:

1. Найти приближенное значение функции 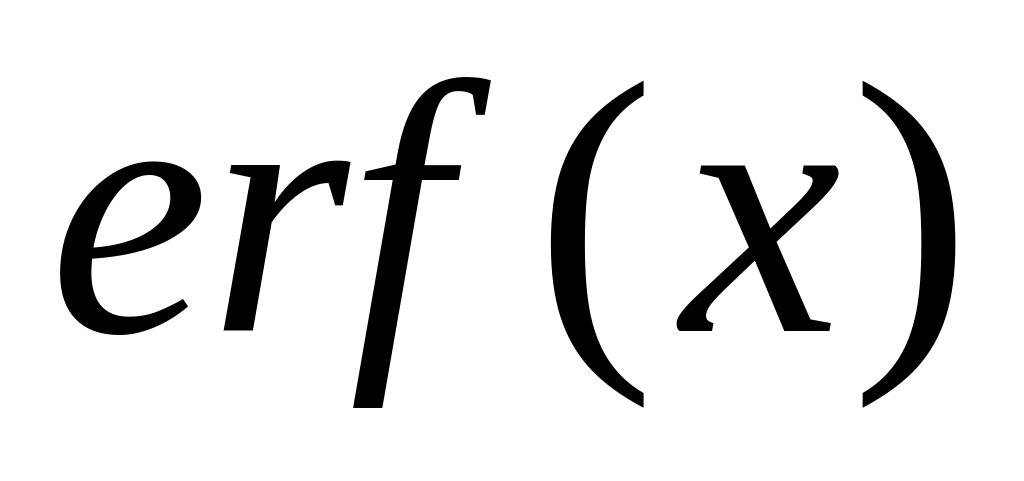, протабулировав на отрезке [a,b] с шагом h с точностью 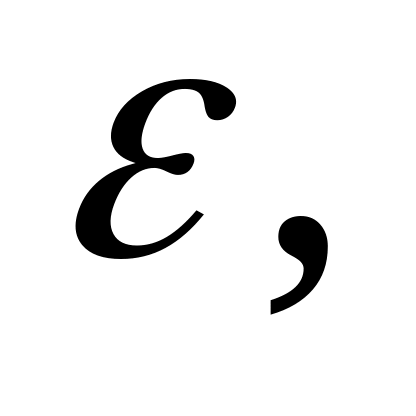основываясь на ряде Тейлора.

2. По полученной таблице значений построить интерполяционный полином Лагранжа, приближающий erf(x)

3. Найти приближенное значение функции , используя

- составную квадратурную формулу Гаусса с двумя узлами;

- составную квадратурную формулу Симпсона;

- формулу трапеций.

4. Построить таблицу обратной к функции

Исходные данные:

a=0, b=2, h=0.2, .

1. Протабулировать erf(x) на отрезке [a,b] с шагом h c точностью ε, основываясь на ряде

Тейлора, предварительно вычислив его:

, где a=0, b=2, h=0.2, .

Каждый последующий член ряда a_n+1 получается из предыдущего члена a_n, умножением на

величину q_n= , т.о. a_n+1 = a_n q_n.

Получилась таблица:

I	x i	f i
0	0	0
1	0.2	0.222703
2	0.4	0.428392
3	0.6	0.603856
4	0.8	0.742101
5	1	0.842701
6	1.2	0.910314
7	1.4	0.952285
8	1.6	0.976348
9	1.8	0.989091
10	2	0.995322

где

Доказательство сходимости ряда:

Теорема. Для всякого степенного ряда существует R ( - число или ) такое, что:

а) если и , то ряд абсолютно вне круга К; этот круг называют кругом сходимости и расходится вне круга K; этот круг называют кругом сходимости ряда, а R – радиусом сходимости ряда;

б) если R=0, то ряд сходится в одной точке x=0;

в) если , то ряд сходится во всей комплексной плоскости.

Доказательство сходимости: Найдем радиус сходимости R по формуле (1). Пусть и , т.к. в формуле (1) присутствует модуль, то (-1)ⁿ и (-1)ⁿ⁺¹ не учитываем.

т.е. ряд сходится во всей комплексной плоскости.

2. По полученной таблице значений построить интерполяционный полином Лагранжа, приближающий erf(X)

и вычислить погрешность интерполирования

ε_n=max ε(x), ε(x)=|erf(x)-L_n(x)|

^xЄ(a,b)

Получилось:

ε_n=0

i	xi	erf(x)	Li(x)	|erf(x)-Li(x)|
0	0	0	1.12838e-006	0
1	0.2	0.222703	0.222703	0
2	0.4	0.428392	0.428393	0
3	0.6	0.603856	0.603857	0
4	0.8	0.742101	0.742101	0
5	1	0.842701	0.842701	0
6	1.2	0.910314	0.910315	0
7	1.4	0.952285	0.952286	0
8	1.6	0.976348	0.976349	0
9	1.8	0.989091	0.989091	0
10	2	0.995322	0.995323	0

Вычислим erf(x) на отрезке с шагом h=0.2 с точностью и L(x). За узлы интерполяции возьмем 11 корней полинома Чебышева. Получаем следующую таблицу значений и графики функции erf(x), L(x).

Получим таблицу:

i	erf(x)	Li(x)	|erf(x)-Li(x)|
0	0	0	0
1	0.222703	0.222703	5.55112e-017
2	0.428392	0.428392	1.66533e-016
3	0.603856	0.603856	1.11022e-016
4	0.742101	0.742101	2.22045e-016
5	0.842701	0.842701	1.11022e-016
6	0.910314	0.910314	1.11022e-016
7	0.952285	0.952285	1.11022e-016
8	0.976348	0.976348	4.44089e-016
9	0.989091	0.989091	3.33067e-016
10	0.995322	0.995322	2.22045e-016

где

xi
1.98769
1.89101
1.70711
1.45399
1.15643
0.843566
0.54601
0.292893
0.108993
0.0123117
1.98769

График погрешностей:

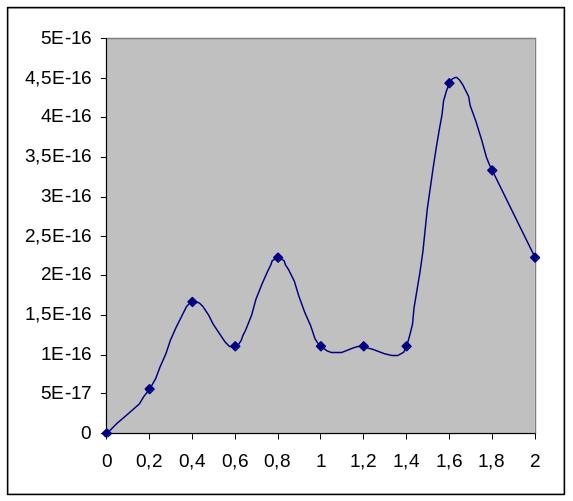
Вычислим erf(x) на отрезке с шагом h=0.1 с точностью и L(x). За узлы интерполяции возьмем 11 корней полинома Чебышева. Получаем следующую таблицу значений и графики функции erf(x), L(x).

Получим таблицу:

i	erf(x)	Li(x)	|erf(x)-Li(x)|
0	0	0	0
1	0.112463	0.112463	2.77556e-017
2	0.222703	0.222703	5.55112e-017
3	0.328627	0.328627	1.11022e-016
4	0.428392	0.428392	1.66533e-016
5	0.5205	0.5205	0
6	0.603856	0.603856	3.33067e-016
7	0.677801	0.677801	0
8	0.742101	0.742101	0
9	0.796908	0.796908	3.33067e-016
10	0.842701	0.842701	1.11022e-016
11	0.880205	0.880205	6.66134e-016
12	0.910314	0.910314	1.11022e-016
13	0.934008	0.934008	1.11022e-016
14	0.952285	0.952285	0
15	0.966105	0.966105	3.33067e-016
16	0.976348	0.976348	1.22125e-015
17	0.98379	0.98379	2.22045e-016
18	0.989091	0.989091	5.55112e-016
19	0.99279	0.99279	2.22045e-016
20	0.995322	0.995322	1.11022e-016

Узлы интерполяции:

xi
1.98769
1.89101
1.70711
1.45399
1.15643
0.843566
0.54601
0.292893
0.108993
0.0123117
1.98769

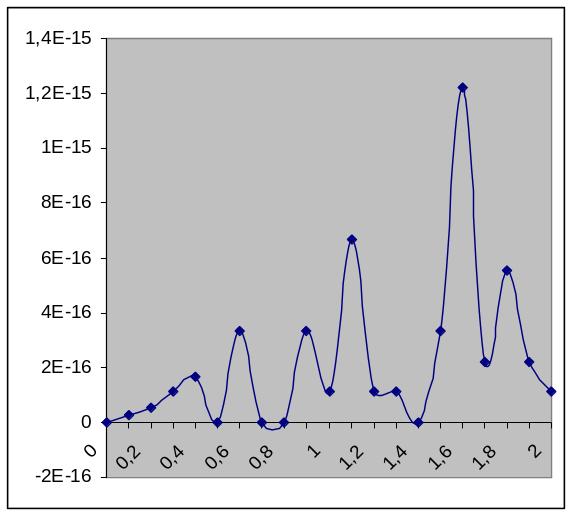
Увеличим количество узлов до 15:

i	erf(x)	Li(x)	|erf(x)-Li(x)|
0	0	0	0
1	0.222703	0.222703	1.38778e-016
2	0.428392	0.428392	1.66533e-016
3	0.603856	0.603856	1.11022e-016
4	0.742101	0.742101	2.22045e-016
5	0.842701	0.842701	5.55112e-016
6	0.910314	0.910314	6.66134e-016
7	0.952285	0.952285	2.22045e-016
8	0.976348	0.976348	4.44089e-016
9	0.989091	0.989091	5.55112e-016
10	0.995322	0.995322	1.11022e-016

Узлы интерполяции:

xi
1.99452
1.95106
1.86603
1.74314
1.58779
1.40674
1.20791
1
0.792088
0.593263
0.412215
0.256855
0.133975
0.0489435
0.0054781

График погрешностей:

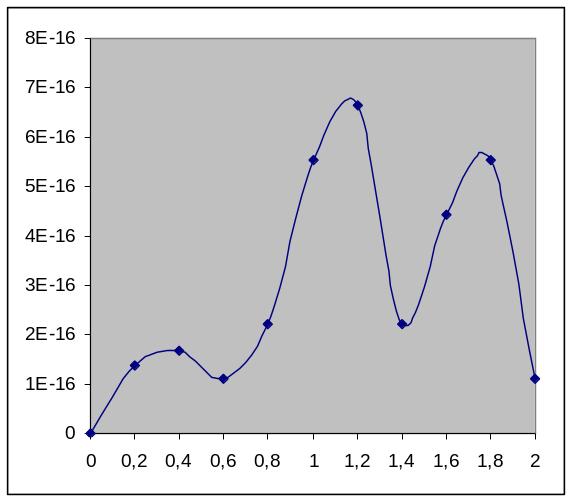
Увеличим количество узлов до 25:

xi
1.99692
1.97237
1.92388
1.85264
1.76041
1.64945
1.5225
1.38268
1.23345
1.07846
0.921541
0.766555
0.617317
0.477501
0.350552
0.239594
0.14736
0.0761205
0.0276301
0.00308267

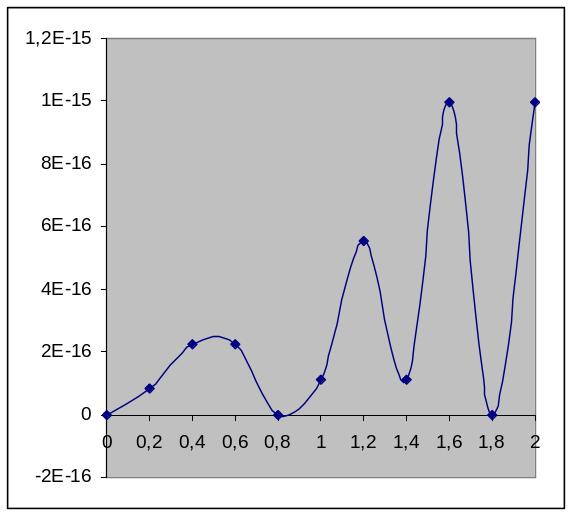
Увеличим количество узлов до 25:

i	erf(x)	Li(x)	|erf(x)-Li(x)|
0	0	0	0
1	0.222703	0.222703	0
2	0.428392	0.428392	0
3	0.603856	0.603856	0
4	0.742101	0.742101	0
5	0.842701	0.842701	0
6	0.910314	0.910314	8,88178e-016
7	0.952285	0.952285	1,55431e-015
8	0.976348	0.976348	1,88738e-015
9	0.989091	0.989091	1,88738e-015
10	0.995322	0.995322	9,65894e-015

Узлы интерполяции:

xi
1.99803
1.98229
1.95106
1.90483
1.84433
1.77051
1.68455
1.58779
1.48175
1.36812
1.24869
1.12533
1
0.874667
0.75131
0.631875
0.518246
0.412215
0.315453
0.229487
0.155672
0.0951729
0.0489435
0.0177127
0.00197327

График погрешностей:

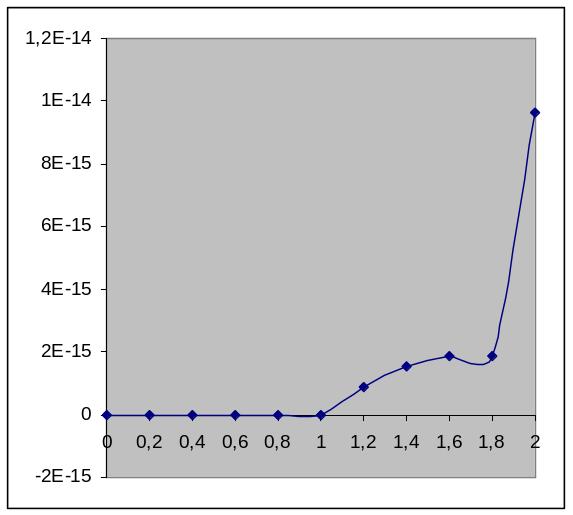
Вывод: Из приведенных графиков ошибок интерполяции видим, что наименьшая погрешность достигается при вычислении по 15-ти чебышевским узлам. Далее, при повышении степени интерполяционного полинома, ошибка начинает быстро возрастать, что свидетельствует о том, что вычислительные свойства интерполяционного полинома делают его неприменимым при достаточно большом числе узлов интерполирования