
- •6. Выносливость конструкции вертолета.
- •6.1.1. Статистический характер выносливости
- •6. 1. 2. Зависимость долговечности от величины .
- •6.1.5. Влияние статической подгрузки.
- •6. 1. 4. Сложное напряженное состояние
- •6. 1. 5. Гипотеза линейного суммирования повреждаемостей.
- •6.1.6. Эквивалентное напряжение
6. 1. 4. Сложное напряженное состояние
Элементы конструкции вертолёта обычно подвержены действию комбинации сил и моментов. При этом переменные силы и моменты имеют среднее значение, не равное нулю, т.е. помимо переменных напряжений создают и статическую нагрузку. При таком нагружении в расчетном сечении имеет место сложное напряженное состояние. Для этого случая также нет общих формул, дающих достоверные результаты.
Для многих вертолётных деталей обычно переменные касательные напряжения значительно меньше нормальных. Их действие учтывают, увеличивая нормальные напряжения по приближенной формуле
![]() (5.5)
(5.5)
Определив значение
![]() и пользуясь, кривой
,
полученной для случая, когда
и пользуясь, кривой
,
полученной для случая, когда
![]() определяют долговечность для
,
большего по величине, чем
определяют долговечность для
,
большего по величине, чем
![]() ,
что позволяет учесть действие касательных
напряжений; не имея результатов испытаний
при
,
что позволяет учесть действие касательных
напряжений; не имея результатов испытаний
при
![]() .
Постоянные касательные
напряжения
.
Постоянные касательные
напряжения
![]() обычно малы и их не учтывают (за исключенем
расчета
валов трансмиссий). Нормальные постоянные
напряжения от различных компонентов
сил и моментов при расчете суммируют,
а далее учитывают так, как это указано
в п. 5.1.3.
обычно малы и их не учтывают (за исключенем
расчета
валов трансмиссий). Нормальные постоянные
напряжения от различных компонентов
сил и моментов при расчете суммируют,
а далее учитывают так, как это указано
в п. 5.1.3.
6. 1. 5. Гипотеза линейного суммирования повреждаемостей.
Величины полуразмахов переменных напряжений, действующих в агрегатах вертолёта, изменяются в зависимости от режима полёта. Поэтому возникает необходимость оценки эффекта последовательного действия переменных нагрузок разной величины. Применяемый для этого расчетный метод основывается на гипотезе линейного суммирования повреждаемостей.
Пусть к образцу
было приложено
![]() циклов нагрузки с полуразмахом
циклов нагрузки с полуразмахом
![]() ,
,
![]() циклов нагрузки с полуразмахом
циклов нагрузки с полуразмахом
![]() и т.д. Обозначим
и т.д. Обозначим
![]() долговечность при действии нагрузки с
полуразмахом
;
долговечность при действии нагрузки с
полуразмахом
;
![]() - долговечность при действии нагрузки
с полуразмахом
и т.д. Предположим, что работа
- долговечность при действии нагрузки
с полуразмахом
и т.д. Предположим, что работа
![]() ,
которую надо произвести, чтобы
разрушить объект, одинакова для всех
процессов
(5. 1) с любым
полуразмахом,
и на каждый цикл нагружения с одинаковым
полуразмахом
,
которую надо произвести, чтобы
разрушить объект, одинакова для всех
процессов
(5. 1) с любым
полуразмахом,
и на каждый цикл нагружения с одинаковым
полуразмахом
![]() приходится одинаковая доля этой работы
приходится одинаковая доля этой работы
![]() .
Работа для всех циклов с полуразмахом
будет равна
.
Работа для всех циклов с полуразмахом
будет равна
![]() .
Сумма работ всех действовавших на объект
циклов нагружения до его разрушения
.
Сумма работ всех действовавших на объект
циклов нагружения до его разрушения
![]() .
Из этого выражения следует условие
разрушения
.
Из этого выражения следует условие
разрушения
![]() .
(5.6)
.
(5.6)
Отношение
![]() называется повреждаемостью.
Соотношение
(5. 6) выражает
гипотезу
линейного
суммирования повреждаемостей.
называется повреждаемостью.
Соотношение
(5. 6) выражает
гипотезу
линейного
суммирования повреждаемостей.
Условие разрушения
(5. 6) является
приближенным. По некоторым экспериментальным
данным разрушение происходит при
![]() .
Многими авторами выдвинуты другие
гипотезы суммирования действия нагрузок
различного уровня, однако эти гипотезы
пока не получили широкого распространения.
Практически с некоторым запасом можно
считать, что разрушение происходит при
.
Многими авторами выдвинуты другие
гипотезы суммирования действия нагрузок
различного уровня, однако эти гипотезы
пока не получили широкого распространения.
Практически с некоторым запасом можно
считать, что разрушение происходит при
![]() .
Этой формулой обычно пользуются, когда
нет более точных экспериментальных
данных.
.
Этой формулой обычно пользуются, когда
нет более точных экспериментальных
данных.
6.1.6. Эквивалентное напряжение
Используя гипотезу
линейного суммирования, можно определить
так называемое эквивалентное
напряжение.
Эквивалентным
называется циклически изменяющееся
напряжение, имеющее постоянный полуразмах
![]() такой величины, при которой повреждаемость
конструкции
такой величины, при которой повреждаемость
конструкции
![]() та же, что при действии циклов напряжений
с полуразмахами различной величины
,
причём число циклов эквивалентного
напряжения (
та же, что при действии циклов напряжений
с полуразмахами различной величины
,
причём число циклов эквивалентного
напряжения (![]() )
и суммарное число циклов (
)
и суммарное число циклов (![]() )
напряжений различной величины одинаковы.
)
напряжений различной величины одинаковы.
Пусть на рассматриваемую деталь действовало циклов нагрузки с полуразмахом , циклов нагрузки с полуразмахом и т. д.
По кривой
найдём долговечность, соответствующую
величине
(т.е. если бы на образец
действовала только переменная нагрузка
с полуразмахом
)
и обозначим её, как и раньше,
![]() .
Далее найдём долговечности:
.
Далее найдём долговечности:
![]() ,
соответствующую
(рис.
5.6б);
,
соответствующую
(рис.
5.6б);
![]() ,
соответствующую
,
соответствующую
![]() и т. д. и повреждаемости
и т. д. и повреждаемости
![]() ,
,
![]() и т.д. Общее число циклов нагрузок всех
уровней:
и т.д. Общее число циклов нагрузок всех
уровней:
![]() .
Суммарная повреждаемость:
.
Суммарная повреждаемость:
![]() .
.
Найдём теперь
эквивалентное напряжение. Так как
![]() ,
а, следовательно,
,
а, следовательно,
![]() и по условию
и по условию
![]() и
и
![]() ,
то
,
то
![]() .
(5.7)
.
(5.7)
Для определения эквивалентного напряжения перепишем (5. 7) в виде
![]() .
(5.8)
.
(5.8)
Из (5.3) следует
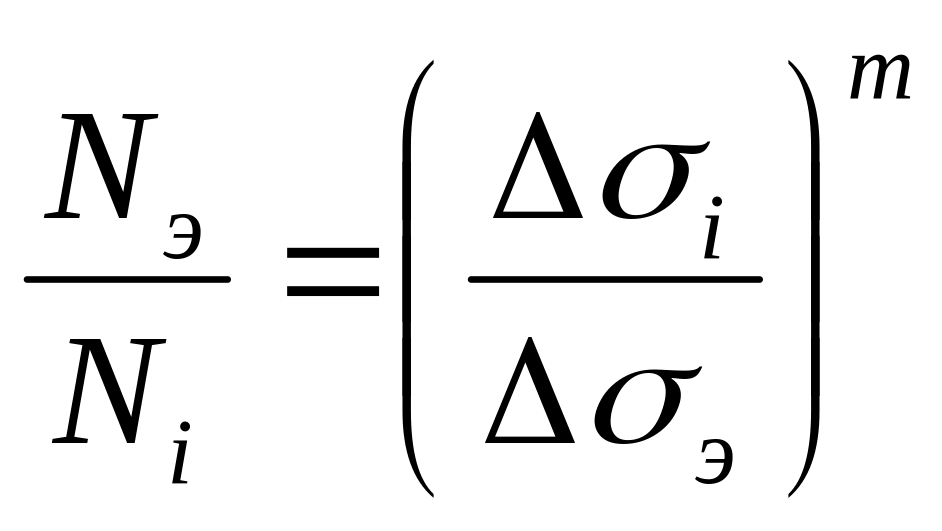 .
(5.9)
.
(5.9)
Подставв
(5.9) в (5.8) и решая отностельно
![]() .
найдем
.
найдем
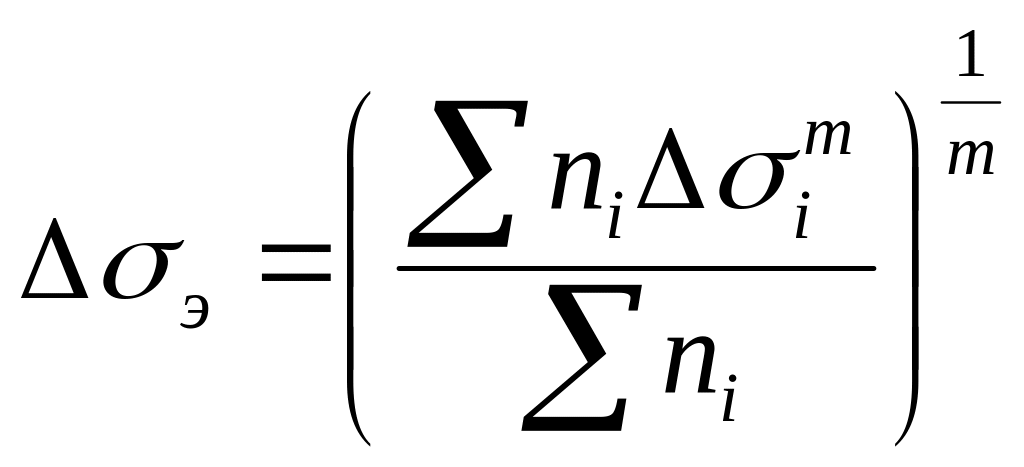
или
![]() ,
,
![]() ,
(5.10)
,
(5.10)
где
![]() - относительное число циклов с полуразмахом
- относительное число циклов с полуразмахом
![]()
(
![]() )
)
