6. 1. 2. Зависимость долговечности от величины .

Повторяя испытания при разных величинах , построим для них кривые . По этим кривым для различных значений и заданного значения и построить график (рис. 5. 3);

- вероятность разрушения в %.

Обычно кривую строят в логарифмических координатах ( , то есть зависимость числа циклов до разрушения от величины полуразмаха . Эта зависимость, особенно при больших значениях , изучена пока недостаточно полно. При кривая для элементов конструкции вертолёта в логарифмических координатах обычно близка к прямой. Очевидно, что уравнение такой прямой будет иметь вид

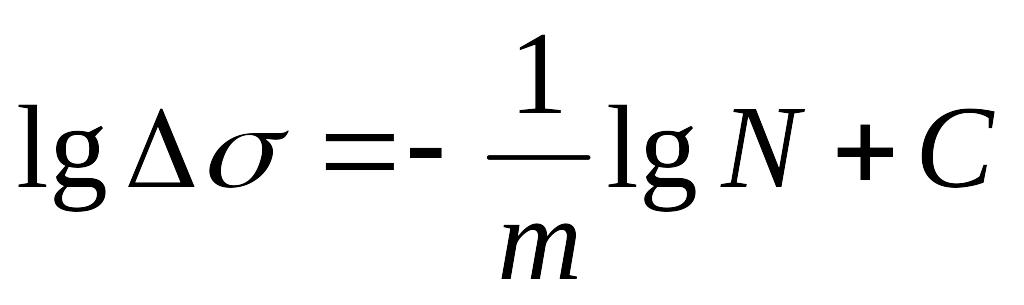, (5.2)

где - есть тангенс угла наклона прямой (5.2) к оси абсцисс.

В сопротивлении материалов вводится понятие предела выносливости , который определяется как такая наибольшая величина полуразмаха , при которой разрушение не происходит ни при каком сколь угодно большом числе циклов нагрузки. Однако в практически важном диапазоне этого предела не существует и, следовательно, нельзя пользоваться понятием «предел выносливости», не указав, до какого числа циклов проведены испытания, а также какой вероятности разрушения он соответствует (рис. 5.4).

Значение, , соответствующее заданным значениям и , называется ограниченным пределом выносливости на базе циклов с вероятностью разрушения .

Правильное представление о кривой для данной детали можно получить только на основании экспериментальных исследований. В случае отсутствия таких данных обычно пользуются приближенным соотношением

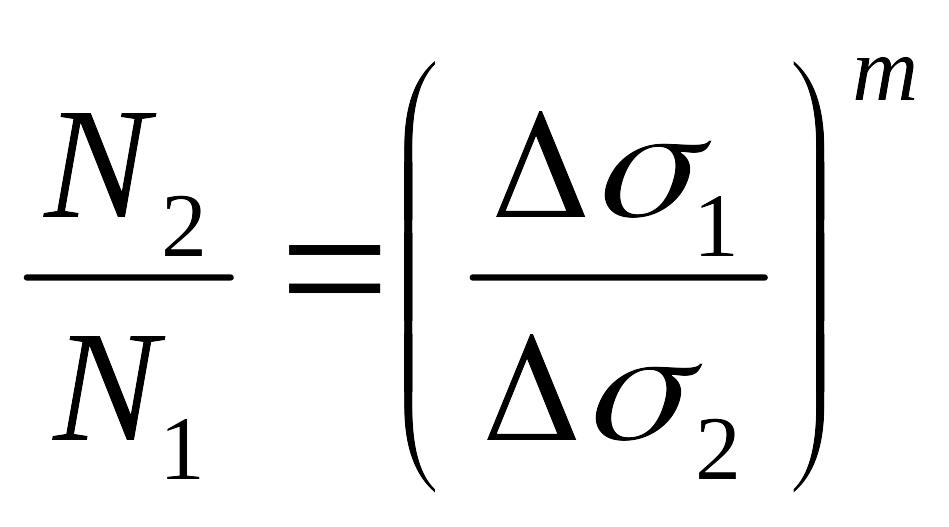, (5.3)

вытекающим из уравнения (5. 2). Значение показателя степени (учитывая, что реальные детали имеют примерно одинаковые концентрации напряжений, одинаковое качество изготовления и т. д. ) можно приближенно принимать при равным , а при больших значениях , - . С помощью этой завсимости можно пересчитать долговечность при изменении полуразмаха переменных напряжений. Однако, хотя бы одна точка этой кривой должна быть найдена экспериментально.

Большая величина показателя степени в формуле (5. 3) означает, что даже при небольшом понижении уровня переменных напряжений долговечность элемента конструкции значительно увеличивается. Поэтому конструктор всегда должен стремиться даже к небольшому (5...10%) понижению уровня переменных нагрузок. Только при этом удаётся сделать конструкцию, имеющую большой ресурс.

6.1.5. Влияние статической подгрузки.

Рассмотрим теперь более сложный случай нагружения, когда напряжение в рассматриваемой точке меняется по закону

(5.4)

Велчина называется напряжением статической подгрузки. Если (растяжение), то долговечность или ограниченный предел выносливости уменьшается тем больше, чем больше . При (сжатие) имеет место обратный эффект. И изменение влияет на долговечность меньше, чем изменение , однако его надо учитывать при определении .

При малых величинах ( ) статической подгрузки, при её увеличении, имеет место значительное снижение предела выносливости. При больших значениях ( ) влияние статической подгрузки уменьшается, а при ешё больших ( ) снова увеличивается. Если известен предел выносливости для , то его можно пересчитать для другого значения по приближенной формуле

,

действительной только в пределах одного участка кривой .

Для среднего участка, кривой (см. рис. 5. 5) коэффициент для остальных деталей и для деталей из алюминиевых сплавов.