Графики полигона частот и гистограммы
Построено в Excel
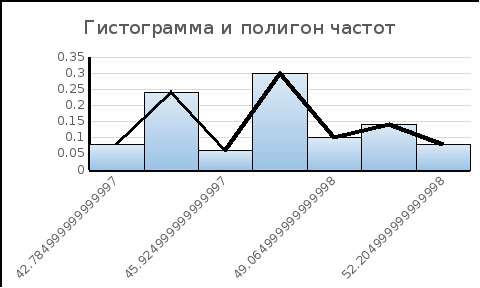
IV.3 Проверка гипотезы о нормальном распределении
Проверяем
гипотезу о нормальном распределении
выборки с помощью критерия Пирсона
(хи-квадрат).
При расчетах будем использовать интервалы
равной вероятности, т.е. интервалы, в
которые случайная величина попадает с
вероятностью
,
где
.
Будем
считать, что функция распределения
принимает
значения от 0 до 1 с шагом 1/7. А функция
интеграла вероятности
.
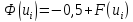Значения
находим по
таблице функции Лапласа.
Ссылка на таблицу: http://www.natalymath.ru/laplas.html
Оценочные границы интервалов равной вероятности найдем по формулам:
.
Значения
вычисляем методом линейной интерполяции:
-
Φ (−∞) =−0,5;
-
Φ (-1,07) =-0,3577<-0,357<-0,3554= Φ (-1,06)
=
-1,07 + (-1,06+1,07) *
= -1,07 + 0,01*
=
-1,06696;
-
Φ (-0,57) =-0,2157<-0,214<-0,2123= Φ (-0,56)
=
-0,57 + (-0,56+0,57) *
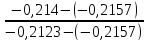= -0,57 + 0,01*
=
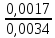-0,565;
-
Φ (-0,18) =-0,0714<-0,071<-0,0675= Φ (-0,17)
=
-0,18 + (-0,17+0,18) *
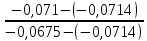= -0,18 + 0,01*
=
-0,17897;
-
Φ (0,18) =0,0714<0,072 <0,0753= Φ (0,19)
=
0,18 + (0,19-0,18) *
= 0,18 + 0,01*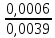
=
0,18154;
-
Φ (0,56) =0,2123<0,215 <0,2157= Φ (0,57)
=
0,56 + (0,57-0,56) *
= 0,56 + 0,01*
=
0,56794;
-
Φ (1,07) =0,3577<0,358 <0,3599= Φ (1,08)
=
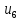1,07 + (1,08-1,07) *
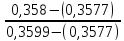= 1,07 + 0,01*
=
1,07136;
8)
Вычислим
по
формуле
Результаты внесем в таблицу:
|
|
F(ui) |
Ф(ui) |
ui |
xi |
|
|
|
1 |
0 |
-0,5 |
- |
- |
Xв= |
47,42 |
|
2 |
0,143 |
-0,357 |
-1,06696 |
44,454 |
S= |
2,78 |
|
3 |
0,286 |
-0,214 |
-0,565 |
45,849 |
|
|
|
4 |
0,429 |
-0,071 |
-0,17897 |
46,922 |
|
|
|
5 |
0,572 |
0,072 |
0,18154 |
47,924 |
|
|
|
6 |
0,715 |
0,215 |
0,56794 |
48,999 |
|
|
|
7 |
0,858 |
0,358 |
1,07136 |
50,398 |
|
|
|
8 |
1 |
0,4 |
+ |
+ |
|
|
Для
проверки гипотезы о нормальном
распределении случайной величины в
качестве меры расхождения между
теоретическим и статистическим
распределениями выберем случайную
величину
(хи-квадрат).
Все полученные значения сводим в таблицу:
|
№ интервала |
Интервал |
𝑛𝑖 |
𝑊𝑖 |
𝑃𝑖 |
𝑛𝑖−𝑁∙𝑃𝑖 |
(𝑛𝑖−𝑁∙𝑃𝑖)^2 |
(𝑛𝑖−𝑁∙𝑃𝑖)^2*/(𝑁∙𝑃𝑖) |
|
1 |
[-б; 44,454] |
7 |
7/50 |
0,143 |
-0,15 |
0,0225 |
0,003 |
|
2 |
[44,454; 45,849] |
9 |
9/50 |
0,143 |
1,85 |
3,4225 |
0,478 |
|
3 |
[45,849; 46,922] |
3 |
3/50 |
0,143 |
-4,15 |
17,2225 |
2,409 |
|
4 |
[46,922; 47,924] |
4 |
4/50 |
0,143 |
-3,15 |
9,9225 |
1,388 |
|
5 |
[47,924; 48,999] |
11 |
11/50 |
0,143 |
3,85 |
14,8225 |
2,073 |
|
6 |
[48,999; 50,398] |
9 |
9/50 |
0,143 |
1,85 |
3,4225 |
0,478 |
|
7 |
[50,398; +б) |
7 |
7/50 |
0,143 |
-0,15 |
0,0225 |
0,003 |
|
∑= |
|
50 |
1 |
1 |
|
|
6,832 |