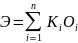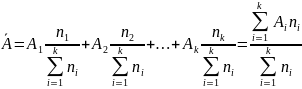6. Метод экспертных оценок финансовых потерь.

Суть метода экспертных оценок состоит в разработке системы параметров, по которым оценивается уровень риска предприятия. Для каждого оценочного показателя установлена его значимость, как правило, в форме весового коэффициента, который отражает его влияние на итоговую величину риска. После этого эксперты по каждому возможному варианту реализации риска для конкретного объекта оценки присваивают некоторое значение в соответствии со значением эталонов (максимально возможного значения параметра).

Пример оценки экспертным методом, согласно методике немецких компаний beri.

Критерий оценки	Весовой коэффициент
Политическая стабильность	12
Защита иностранных инвестиций	6
Степень национализации экономики	6
Вероятность девальвации национальной валюты	6
Состояние платежного баланса страны	6
Степень развития бюрократии	4
Темпы экономического роста	10
Конвертируемость национальной валюты	10
Качество исполнения договора	6
Уровень расходов на зарплату и повышение производительности труда	8
Возможность использования оценок и услуг внешних и внутренних экспертов и аудиторских компаний	2
Эффективность организации коммуникаций	4
Взаимоотношения субъектов хозяйствования с государственными структурами, связь с обществом	4
Условие получения внешних и внутренних кредитов	8

На сегодняшний день экспертная оценка в ситуациях, связанных с недостатком формальной информации при разработке инновационных проектов, а также принятия стратегических решений, которые характеризуются степенью высокой неопределенности, относящимся к обязательным методам анализа рисков.

7. Статистический и аналитический методы оценки.

Суть статистических методов основана на теории распределения случайных величин. Предполагается, что при наличии достаточно большого объема статистических данных об изучаемом объекте, наибольшую частоту построений имеют параметры, значения которых максимально близки к средней величине, тогда как вероятность получения крайних значений близка к нулю. Такое распределение относят к группе нормальных распределений.

Ā – среднее значение финансового показателя.

1. 

k – общее число значений оцениваемого показателя, который он принимает по рассматриваемой выборке.

А_i – величина фактического показателя с частотой появления n_i.

2. R – размах вариации финансового показателя

R = A_max – A_min

A_max – максимальная величина выборки.

3. σ² – дисперсия степени риска.

4. Среднее квадратическое отклонение

σ показывает степень разброса случайных величин относительно среднего значения финансового показателя.

Так как реализация рискового события носит неопределенный характер, величина среднего квадратического отклонения характеризует степень неопределенности при реализации проекта.

Для двух проектов с одинаковым математическим ожиданием финансового результата выбирают тот проект, дисперсия по которому принимает меньшее значение.

5. Коэффициент вариации

Ā_ср – среднее значение ожидаемого финансового роста.

V_R – относительная величина.

По физическому смыслу коэффициент вариации выражает количество риска, приходящегося на единицу доходности проекта. Таким образом, по степени охвата этот показатель относится к комплексным.

Для коэффициента вариации установлены следующие пороговые значения:

1. V_R<10% – характеризует процессы с малой волатильностью (уровень риска минимальный);

2. 10<V_R<25% – умеренная колеблемость (допустимый риск);

3. 25<V_R<50% – высокая волатильность (критический уровень риска);

4. 1V_R>50% – такие процессы характеризуются недопустимой волатильностью (уровень риска относится к группе катастрофических).

Пример

Допустим, что при продвижении инновационного продукта маркетинговые … А в 200-х случаях приносило следующий финансовый результат:

1. 55 – Пр=230 тыс.руб.

2. 80 – Пр=260 тыс.руб.

3. 65 – Пр=300 тыс.руб.

Б 200

1. 70 – Пр=210 тыс.руб.

4. 60 – Пр=330 тыс.руб.

5. 70 – Пр=380 тыс.руб.

1. R_А=300-230=70 тыс.руб.

R_Б=380-210=170 тыс.руб.

А: 1) P_i = 55/200 = 0,275

2) P_i = 0,4

3) P_i = 0,325

Б: 1) P_i = 0,35

2) P_i = 0,3

3) P_i = 0,35

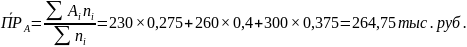
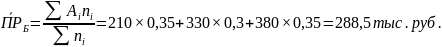
ПР – математическое ожидание по полученной прибыли.

3.

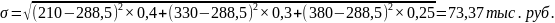
4.

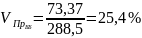
А)

Таким образом, с вероятностью 68,3% можно утвердить, что значение прибыли по данному проекту будет находится в пределах от 238 тыс. руб. до 292 тыс. руб. С вероятностью 95,5% от 210 тыс. руб. до 319 тыс. руб. с вероятностью 99,73% прибыль лежит в пределах от 183 тыс. руб. до 347 тыс. руб.

Б)

Анализ второго проекта показывает, что с вероятностью 68,3% значение прибыли инвестора будет находиться от 215 до 362 тыс8. руб., с вероятностью 95,5% - от 142 до 435  тыс. руб., с вероятностью 99,73% - от 68 до 508 тыс. руб.

Коэффициент корреляции, рассчитанный выше, по своему физическому смыслу отображает величину риска, приходящийся на единицу доходности проекта.

Достоинства и недостатки метода:

1. С помощью расчета статистических показателей рисков (математическое ожидания, дисперсии, коэффициента ковариации) можно оценить не только степень риска по отдельному инвестиционному проекту, но и величину неопределенности по всей предпринимательской деятельности предприятия в целом (взято за анализируемый показатель значения выручки, рентабельности, прибыли или других) – достоинство.

2. Достоинством статистического метода является также относительная простота расчетов, наличие агрегированных показателей риска, то есть обобщающих.

Недостатком является необходимость накапливания достаточно большого количества статистических данных за ретроспективный период, причем объем собранной информации напрямую влияет на точность производимых расчетов.

3. Величина среднеквадратического отклонения показывает степень разброса ключевого показателя (например, прибыли) относительно ее среднего ожидаемого значения, но не отображает направления, в котором преимущественно может находиться анализируемая величина.

В формуле для подсчета дисперсии стоит квадрат разницы фактического и ожидаемого значения анализируемого показателя. В то же время при принятии решений важен знак (наиболее вероятный) этого отклонения, показывающий вероятность потерь или сверхприбыли по проекту.

4. Хотя дисперсия достаточно эффективный инструмент меры риска возможны варианты, когда два проекта с одинаковым математическим ожиданием и значением дисперсии не является в равной мере одинаково рисковыми, особенно это касается риска банкротства, при анализе которого величина риска по проекту напрямую зависит от величины исходного капитала, что не отображается статистическими показателями рисков по проекту.

Аналитический метод

Основой аналитического метода является оценка ключевых параметров изучаемого объекта, значения которых принимаются индикатором уровня риска.

Этапы анализа:

1. Выбор определенных параметров оценки, по уровню которых будет приниматься заключение о степени риска.

2. Определение основных факторов, влияющих на значение ключевых параметров, приведение в нормальный вид зависимости между ними.

3. Оценка характера изменений выбранных параметров под влиянием факторных переменных (анализ чувственности).

4. Расчет узловых или критических значений выбранных параметров, на основе которых определяются допустимые границы риска, его максимальная и минимальная приемлемая величина.

Пр = N – S = P×Q – (V×Q + C)

P – цена;

Q – объем;

V – переменные издержки; совокупность влияющих факторов

C – постоянные издержки.

Критическим узлом является:

Пр (Q) = 0

P(Q_кр) – (V×Q_кр + C) = 0

Q_кр = C/(P –V)

Q^ЗАП = Q² – Q^кр

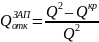– запас безубыточности по относительной величине

Q² – планируемый объем производства

Точку безубыточности (Q^кр) считают границей допустимого уровня риска.