7. Напряжения при растяжении и сжатии.

В сопротивлении материалов основным изучаемым элементом конструкции является брус – тело, у которого один из линейных размеров (длина) значительно превышает два других, определяющих поперечное сечение. При работе конструкции ее элементы воспринимают внешние силы и действие их передают друг другу.

Классификация внешних нагрузок

Внешние силы делятся на активные и реактивные (реакции связей). Активные связи принято называть нагрузками. По способу приложения нагрузки бывают объемные и поверхностные, распределенные исосредоточенные, по характеру изменения в процессе приложения – статические, динамические иповторно-переменные, по продолжительности действия – постоянные и временные.

Внутренние силовые факторы

В процессе деформации бруса, под нагрузкой происходит изменение взаимного расположения элементарных частиц тела, в результате чего в нем возникают внутренние силы. По своей природе внутренние силы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций. Для определения этих сил применяют метод сечений: надо мысленно рассечь брус, находящийся в равновесии, на две части и рассмотреть равновесие одной из них.

П од действием внешних нагрузок в поперечном сечении бруса возникают следующие внутренние силовые факторы (рис. 2.1):

N_z = N - продольная растягивающая (сжимающая) сила 

M_z = T - крутящий (скручивающий) момент

Q_x (Q_y) = Q  - поперечные силы 

M_x (M_y) = M - изгибающие моменты

К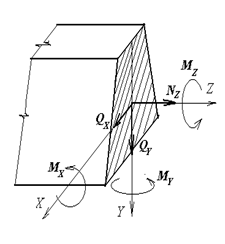 аждый внутренний силовой фактор определяется из соответствующего уравнения равновесия оставшейся после рассечения бруса части (уравнения статики):

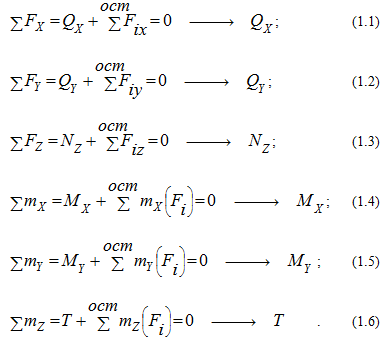
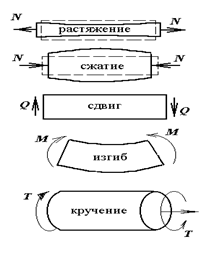
Основные виды нагружения

При простейших случаях нагружения бруса в его поперечных сечениях возникает один внутренний силовой фактор (Рис. 2.2).

Если в поперечном сечении бруса имеет место только внутренняя продольная сила N, такая деформация называется растяжением/сжатием;

Если в сечении бруса возникает только внутренний крутящий момент T, то такая деформация называется кручением (скручиванием);

Изгиб - вид нагружения, при котором в поперечных сечениях бруса действует изгибающий момент M.

Случай, когда в поперечных сечениях бруса есть только поперечная сила Q называется сдвиг.

Рис. 2.2 - основные виды деформации

8. Закон Гука, модуль упругости, коэффициент Пуассона.

Закон Гука записывается для малых напряжений и деформаций и имеет вид простой пропорциональности. Для тонкого растяжимого стержня закон Гука гласит “перемещения прямо пропорциональны нагрузкам“ и имеет вид: F=k

Здесь F сила натяжения стержня,  — его удлинение, а k называется коэффициентом упругости или жёсткостью.

Очевидно, что коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Полезно выделить зависимость от размеров стержня (площади поперечного сечения A и длины L ) явно, записав коэффициент упругости как k=LEA. Величина E – это коэффициент пропорциональности, названным модулем Юнга и зависит только от свойств материала. Полезно теперь ввести относительное удлинение ε=∆l/L и нормальное напряжение в поперечном сечении σ=F/A. В этих обозначениях закон Гука записывается как =E .

Величину, обратную жёсткости, называют податливостью.

На практике часто необходимо найти удлинение стержня под действием растягивающих или сжимающих нагрузок. Подставим в формулу σ=Eε выражения σ=N/A и ε=∆l/L. Тогда l=NLEA

Эта формула справедлива для случая действия одной сосредоточенной силы. Если на стержень действует несколько сил – то стержень разбивается на несколько участков (от силы до силы) и полное удлинение равно сумме удлинений каждого участка в отдельности. l= ni=1NiliEAi 

Закон Гука не является точным законом. Для стали отклонения от пропорциональности между σ и ε незначительны, тогда как чугун или резина явно этому закону не подчиняются. Для них ε = φ(σ), причем φ(σ) может быть аппроксимирована линейной функцией лишь в самом грубом приближении.

Коэффициент Пуассона (коэффициент поперечной деформации) - показывает зависимость между продольными и поперечными деформациями элемента, характеризует упругие свойства материала.

Обозначается строчными греческими буквами ν или μ и является безразмерной величиной.

Определяется отношением относительных поперечных ε_поп и продольных ε_пр деформаций бруса (элемента):

Порядок определения коэффициента поперечной деформации:

Рассмотрим деформацию элемента цилиндрической формы (рис. 1) который до нагружения имеет следующие размеры:

Рис. 1. Размеры бруса до нагружения

здесь

h₀ - начальный продольный размер;

d₀ - начальный поперечный размер (в данном случае - диаметр).

После нагружения некоторой продольной системой сил (например сжимающей) брус изменит свои размеры, продольный размер уменьшится (т.к. сжатие) а поперечный наоборот увеличится (рис. 2).

Р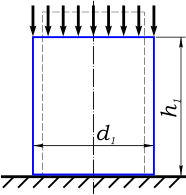 ис. 2. Размеры бруса после деформации

Полученные в результате деформации размеры обозначим соответственно h₁ и d₁, где: h₁=h₀ – Δh d₁=d₀ + Δd

здесь Δh и Δd соответственно абсолютные продольные и поперечные деформации.

Отношение абсолютных деформаций к соответствующим начальным размерам покажет относительные деформации:

а их отношение в свою очередь определяет коэффициент Пуассона материала бруса.

Значение коэффициента принимается по модулю, т.к. продольная и поперечная деформации всегда имеют противоположные знаки (удлинение бруса приводит к его сужению и наоборот).