52. Логические автоматы, способы их задания, синтез двоичного сумматора.
Описывая устройство с одним входом и одним выходом, можно использовать автомат, имеющий несколько входных и выходных каналов. Действительно, каждый символ входного и выходного алфавитов А и В можно закодировать набором длины n и m соответственно из более узкого алфавита, например {0,1}. Тогда автомат будет иметь n входных и m выходных каналов. Через xi(t), где i = 1, 2, …, n, обозначим сигнал, поступающий на i-й входной канал в начале t-го такта, а через уj(t), где j = 1, 2, …, т, – выходной сигнал на j-м канале по окончании t-го такта. Тогда можно считать, что автомат вычисляет сразу т автоматных функций f1, f2, …, fт, каждая из которых зависит от п аргументов (быть может, не от всех существенно). Если же состояния автомата также кодировать наборами длины k в алфавите {0,1}, то его можно будет задать канонической системой уравнений вида
где функции выходов Y1, Y2, …, Ym и переходов Q1, Q2, …, Qk – некоторые логические (булевы) функции. Конечный детерминированный автомат называется логическим автоматом, если его функции выходов и переходов являются логическими функциями.
Пример. Рассмотрим автомат с входным и выходным алфавитом {0,1}, заданный системой уравнений
q1(t – 1) |
q2(t – 1) |
x(t) |
q1(t) |
q2(t) |
y(t) |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
где – отрицание х. Эта система канонической не является. Требуется получить его каноническую систему. Заметим, что данный автомат выполняет следующие преобразования входных сигналов: если номер такта равен 1, 4, 7, …, то автомат «инвертирует» входной сигнал; если номер такта равен 2, 5, 8, …, то входной сигнал поступает на выход автомата без изменений; в остальные такты автомат выдает 0. В бесконечном дереве автоматной функции, вычисляемой этим автоматом, имеется три класса попарно неэквивалентных вершин. Поэтому данный автомат имеет три состояния. Его диаграмма Мура изображена на рисунке. Начальное состояние 0 закодировано парой 00, состояние 1 – парой 01, состояние 2 – парой 10. Такое правило кодирования состояний приводит к канонической таблице
Из
неё уже нетрудно получить каноническую
систему
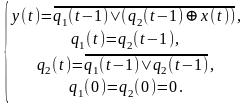
Данный автомат является логическим, поскольку в правой части всех канонических уравнений содержатся только булевы функции. Заметим, что при ином выборе кодировки состояний автомата его каноническая таблица и канонические уравнения будут иметь другой вид.
Простейшим
логическим автоматом является единичная
задержка (т.е. задержка на один такт). В
первый такт работы этот автомат посылает
на выход сигнал 0, а в каждый последующий
такт сигнал на выходе равен входному
сигналу от предыдущего такта, т.е.
y(t + 1) = x(t).
Единичную задержку можно задать
канонической системой
Она моделирует работу простейшего элемента памяти.
Функциональный блок любого логического автомата можно синтезировать из функциональных элементов, а его память – из рассмотренных выше единичных задержек.