50. Детерминированные и недетерминированные функции, примеры, способы задания.

Определение. Функция f F_k называется детерминированной, если для любого натурального t и любых двух последовательностей таких, что , у соответствующих последовательностей и первые t элементов тоже совпадают, т.е. .

Если функция является детерминированной, то для каждого t значение элемента у(t) однозначно определяется «прошлыми» входными значениями х(1), х(2),…, х(t – 1) и «настоящим» значением х(t), но не должно зависеть от «будущих» значений х(t + 1), х(t + 2), … .

Пример. Пусть требуется задать с помощью дерева детермини­рованную функцию f F₃, выходная последовательность которой за­дана равенством у(t) = х(t) + 1 (mod 3), а элементы входной последова­тельности х(t) {0, 1, 2}.

Рассмотрим ориентированное от корня дерево, «растущее» бесконечно вверх. Корнем дерева является вершина v₀. Из каждой вершины выходит по три дуги.

Дуги, имеющие общее начало, пронумерованы слева направо числами 0, 1, 2, означающими одно из трех возможных значений элемента х(t) входной последовательности. Каждая входная последовательность порождает в дереве бесконечную ориентированную цепь, выходящую из вершины v₀. Кроме номера каждая дуга имеет вторую метку, которая показывает соответствующее значение элемента у(t) выходной последовательности при условии, что элемент х(t) равен номеру дуги. Таким образом, пара чисел на дуге дерева, задающего детерминированную функцию, напоминает пару меток на дуге диаграммы Мура для конечного детерминированного автомата. Однако более удобным является представление функции в виде конечного дерева, которое можно получить из бесконечного, удаляя повторяющиеся фрагменты: в дереве, представленном на рисунке, каждую из вершин v₁, v₂ и v₃ можно рассматривать как корень бесконечного дерева, «растущего» вверх из этой вершины и являющегося поддеревом исходного дерева. Нетрудно видеть, что все эти три поддерева эквивалентны исходному дереву, т.е. при совмещении всех четырех поддеревьев метки на их дугах полностью совпадают. Поэтому из исходного дерева можно удалить поддеревья, растущие из вершин v₁, v₂ и v₃, сохранив сами эти вершины. В результате получим конечное дерево, изображенное на рисунке. По нему можно восстановить исходное бесконечное дерево. Поэтому конечное дерево однозначно задает ту же детерминированную функцию.

Далее вершины исходного бесконечного дерева будем называть эквивалентными, если эквивалентны растущие из них бесконечные поддеревья. В дереве детерминированной функции все вершины можно разбить на классы эквивалентности. В рассмотренном примере все вершины попали в один класс эквивалентности, потому что все они эквивалентны между собой. Однако в дереве большинства детерминированных функций можно выделить несколько классов эквивалентности вершин.

Определение. Количество классов эквивалентности вершин в бесконечном дереве детерминированной функции называется весом этой функции.

51. Ограниченно-детерминированные (автоматные) функции, способы их задания.

Определение. Количество классов эквивалентности вершин в бесконечном дереве детерминированной функции называется весом этой функции.

Определение. Детерминированная функция из класса F_k называется автоматной (или ограниченно-детерминированной) функцией, если она имеет конечный вес.

Автоматную функцию можно задать диаграммой Мура. Число вершин в ней равно весу автоматной функции, а сама диаграмма получается из конечного дерева с помощью отождествления в нем эквивалентных вершин.

Пример. Пусть требуется найти вес и построить диаграмму Мура автоматной функции f F₂, выходная последовательность которой задана равенством у(t) = 

Заметим, что в данном случае х(t), у(t) {0, 1}.

На рисунке изображены четыре нижних яруса вершин бесконечного дерева, задающего функцию f.

Все дуги помечены парой чисел x(t), у(t). Кроме того, каждая вершина имеет числовую метку 0 или 1. Вершины с одинаковой меткой принадлежат одному классу эквивалентности, причем нулем помечен корень исходного дерева и все эквивалентные ему вершины. Таким образом, заданная функция имеет вес, равный двум. Следовательно, она является автоматной функцией и может быть задана конечным деревом. В нем должно быть ровно по одной внутренней вершине из каждого класса эквивалентности. Все остальные его вершины должны быть концевыми. Такое конечное дерево всегда позволит восстановить исходное бесконечное дерево. Конечное дерево, задающее автоматную функцию из примера 2, представлено на рисунке.

Теперь, чтобы получить диаграмму Мура для заданной автоматной функции, нужно в конечном дереве отождествить вершины с одинаковыми метками. В данном случае диаграмма Мура будет иметь две вершины и четыре дуги . Следовательно, существует конечный детерминированный автомат, способный вычислять заданную автоматную функцию. Начальным состоянием является 0.

Всякую автоматную функцию можно задать канонической системой уравнений вида

где функция Y – это функция выходов, Q – функция переходов, q(0) – начальное состояние автомата, вычисляющего данную автоматную функцию, а q(t – 1) и q(t) – состояния, в которых оказывается этот автомат соответственно в начале и в конце t-го такта. При этом предполагается, что множество состояний автомата V = {0, 1, 2, …, r – 1}. Функцию, рассмотренную в примере, можно задать канонической системой 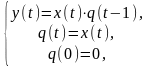где х(t), у(t), q(t) {0, 1}.