Курвіметра і палетки

Звідси випливає залежність:

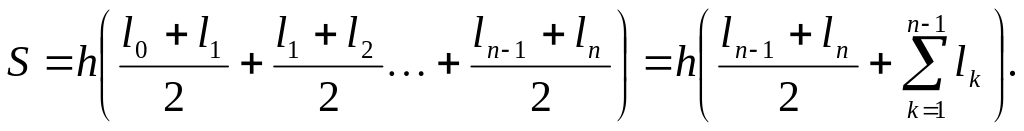
Врахувавши, що в нашому випадку положення палетки на контурі (див. рис. 7.5) L₀=l_n = 0, матимемо

(7.6)

де h - відстань між лініями палетки.

Отже, площа контуру на плані в см² дорівнює добутку суми довжин паралельних відрізків палетки, які знаходяться всередині контуру, на відстань між лініями палетки.

Розглянутий спосіб у випадках невеликих площ і контурів зі складним обрисом незручний і неточний. В інших випадках він дає задовільні результати. Точність визначення площ цим способом становить 1-2 %.

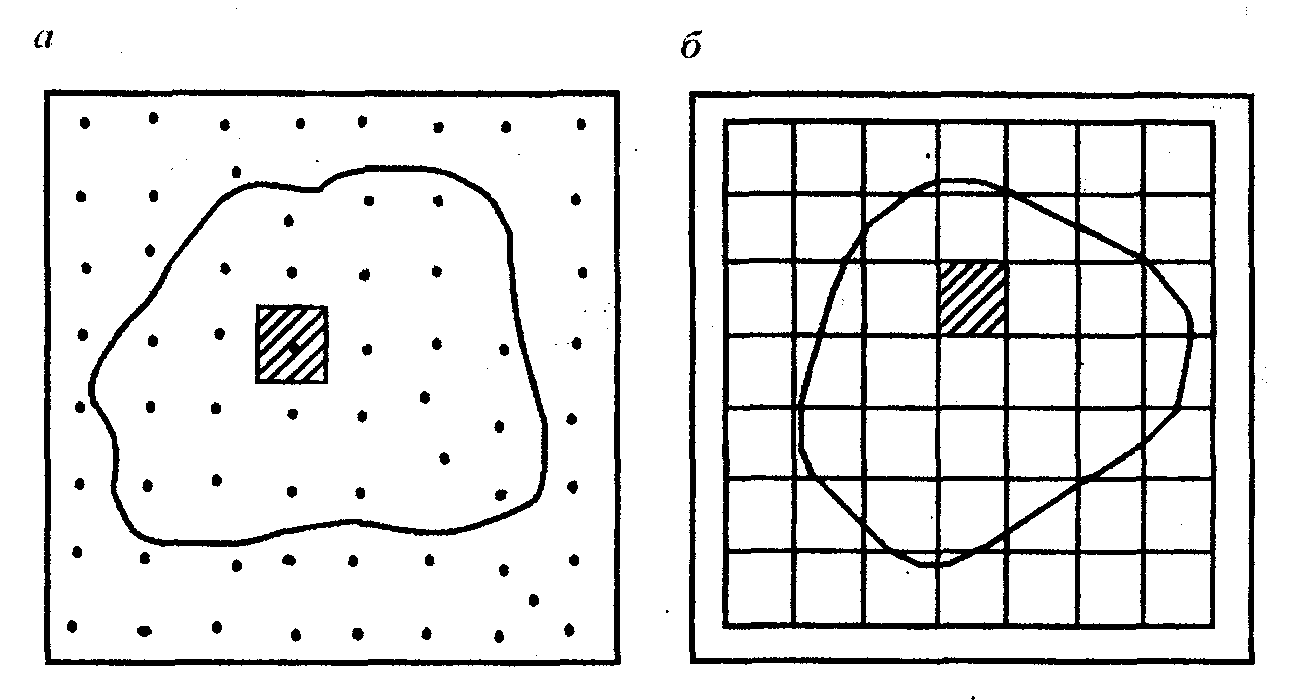
Часто для вимірювання площ використовують точкову, або квадратну палетку (рис. 7.6).

Палетку накреслюють на прозорому папері. Відстань між точками приймають 0,5; 1,0, або 2,0 см залежно від розміру ділянки. Для невеликих площ - 3-4 дм² використовують сантиметрову палетку, в інших випадках - двосантиметрову. Бажано, щоб, всередині контуру, площа якого визначається, було не менше 50 точок палетки.

Рис. 7.6. Палетки для визначення площі: а - точкова; б - квадратна

Для вимірювання площі палетку довільно накладають на контур плану і підраховують кількість точок чи квадратів всередині контуру (n) і кількість точок, що знаходяться на самому контурі (k). Площа, обмежена контуром, дорівнює см². Дійсну площу обчислюють за формулою:

де q - площа одного квадрата палетки (м²) в масштабі плану.

Площу, зазвичай, визначають тричі, по-різному орієнтуючи палетку відносно контуру, і знаходять середнє арифметичне цих трьох визначень. Його й приймають за шукану площу.

7.3.2.3. Визначення площі топографічної поверхні (спосіб в. І. Баумана)

При підрахунку запасів пластових родовищ зі змінними кутами падіння доводиться Мати справу із складними (топографічними) поверхнями, площі яких необхідно визначати. Для цього, а також для розв'язування ряду інших гірничотехнічних задач, поверхні пластів зображують в ізогіпсах. Поверхню, розміщену між двома сусідніми ізогіпсами, вважатимемо лінійчатою, тобто такою, яка у вертикальному перерізі по лінії, перпендикулярній до простягання ізогіпси, зображується похилим відрізком прямої.

Нехай на рис.7.7,а зображена горизонтальна проекція смуги топографічної поверхні, розміщеної між суміжними ізогіпсами 100 і 150 м, а на рис. 7.7,б - її вертикальний переріз по лінії аb.

Рис. 7.7. До визначення площі лінійчатої поверхні: а - план; б - розріз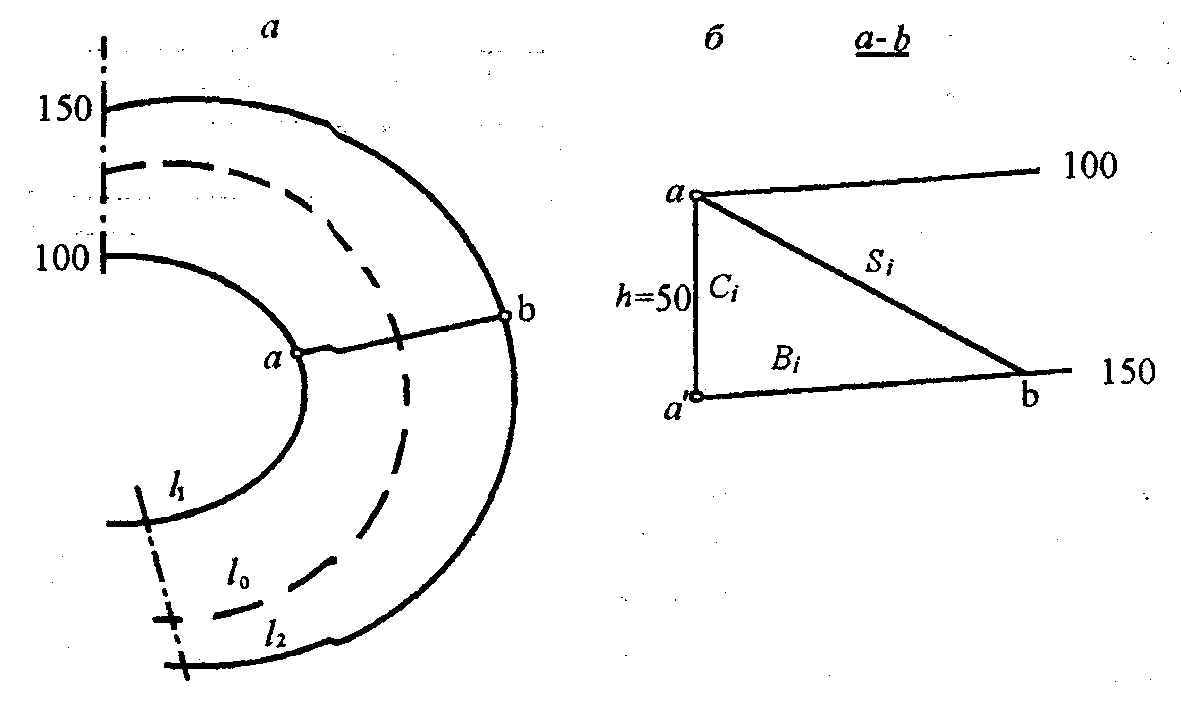

Позначимо через; S_і - дійсну площу смуги топографічної поверхні, яка знаходиться між ізогіпсами І₁ і 1₂ в межах технічних границь; В_і -площу цієї смуги в плані. Спроектуємо S_і на вертикальну циліндричну поверхню, побудовану на середній ізогіпсі l₀.

Висота цієї поверхні дорівнює різниці відміток ізогіпси l₁ і l₂. В нашому випадку h = 50 м. Площу цієї проекції позначимо через C_i. Очевидно, що

C_i=hl₀ ,м², (7.7)

де - довжина середньої ізогіпси, м

При цьому вважають, що кут нахилу лінійчатої поверхні між сусідніми ізогіпсами l₁ і l₂ не змінюється і дорівнює середньому його значенню, визначеному для даної смуги. Дійсну площу S_i смуги лінійчатої поверхні визначають за формулою В. І. Баумана:

, м (7.8)

де B_i - площа смуги лінійчатої поверхні в плані, м²; C_i - площа смуги лінійчатої поверхні в проекції на вертикальну поверхню, м².

Дійсна площа S поверхні пласта, зображеної гіпсометричним планом, дорівнює сумі площ усіх смуг, які знаходяться між сусідніми ізогіпсами, визначених за формулою В. І. Баумана:

Площу S_i кожної смуги визначають в такій послідовності:

- одним із відомих способів визначають на плані площі В_i смуг, які знаходяться між сусідніми ізогіпсами l₁ і l₂, l₂ і l₃,..., l_n-1 і l_n;

- в межах вимірюваної площі курвіметром знаходять довжини ізогіпс l₁,l₂,..., l_n;

- за формулою (7.7) обчислюють площі С_i, проекцій площ смуг на вертикальну поверхню;

- за формулою (7.8) обчислюють дійсні площі S_i смуг, які знаходяться між двома сусідніми ізогіпсами;

- додавши площі окремих смуг, знаходять загальну площу поверхні пласта в контурі підрахунку.

Дослідження показали, що для кутів падіння від 35° до 55° похибка визначення площі поверхні цим способом не перевищує 1 %.