Растяжение-сжатие. Расчёты на прочность по допускаемым напряжениям и по предельной нагрузке.
Условие прочности при растяжении сжатии
Условие прочности при растяжении (сжатии) выражается неравенством:
где [σ] – допускаемые напряжения, определяются как:
n – коэффициент запаса прочности, устанавливаемый нормативными документами.
Условие прочности позволяет решать три типа задач:
1. Проверка прочности (проверочный расчет)
2. Подбор сечения (проектировочный расчет)
3. Определение грузоподъемности (допускаемой нагрузки)
Кручение. Расчёты на прочность.
Кручение это такой вид сопротивления, при котором внешние силы в поперечном сечении формируют только один внутренний силовой факторт Nx.
В расчетах на прочность скручиваемых стержней применяется условие прочности по касательным напряжениям, вызванным кручением:
где [ 
] -
допускаемое касательное напряжение,
[
] =
пред/ KР .
Для пластичных материалов [ ] можно найти, используя в качестве предельного напряжения T - предел текучести при чистом сдвиге.
Геометрические характеристики сечений.
Прямоугольное сечение
Сечение
равнобедренный треугольник.
Сечение прямоугольный треугольник.
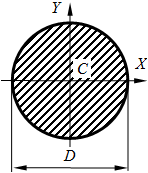
Сплошное круглое сечение.
Полукруглое сечение.
Четверть
круглого сечения.
Кольцевое сечение.
Сечение трубы.
Изгиб. Расчёты на прочность и жёсткость.Расчёт на устойчивость. Формулы Эйлера и Ясинского
Формула Ясинского
Когда формула Эйлера неприменима (за приделом упругости) для определения критической силы можно воспользоваться эмпирической формулой Ясинского П.Ф.
, 
(7)
Здесь 
и 
коэффициенты,
зависящие от материала стержня,
измеряются в МПа, приводятся в
справочниках: для ст. 3 
Формула Эйлера.
,
где Е – модуль Юнга; 
–
минимальный главный центральный момент
инерции поперечного сечения стержня
(очевидно, что при потере устойчивости
изгиб стержня произойдет в плоскости
наименьшей изгибной жесткости); 
–
коэффициент приведения длины, зависящий
от формы потери устойчивости; l – длина
стержня. Произведение 
- приведенная
длина стержня.
Расчет на прочность при изгибе с кручением
Расчёт на прочность при ударе
Установлено, что практически во всех случаях силы динамического воздействия пропорциональны статическим, в связи с чем расчеты на прочность и жесткость при динамических нагрузках выполняются по методам, разработанным для статических, но с введением соответствующих значений динамических коэффициентов. Таким образом, учитывая это, имеем
(15.1)
,
где 
-
динамический коэффициент.
Условия прочности и жесткости применительно к расчету по методу допускаемых напряжений имеют соответственно вид
(15.2)
.