2.2. Расчет наблюдающего устройства

Наблюдающее устройство целесообразно применять в системах модального управления. Рассчитаем параметры наблюдателя для системы модального управления, разработанной в пункте 1.2.

Расчет проводится в следующей последовательности:

• задать элементы матрицы N в общем виде, найти выражения элементов для матрицы динамического компенсатора (2.6) и записать уравнение в скалярной форме. Учитывая матрицы объекта управления (рис.1.1) А и С, запишем в общем виде матрицу динамического компенсатора

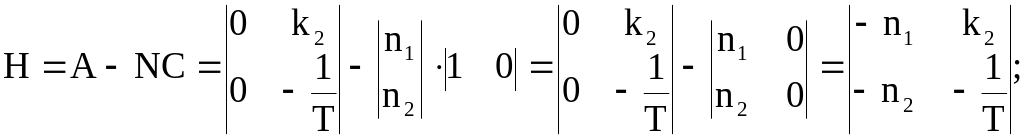
(Примечание) Произведение матриц

, где

• в соответствии с уравнением (2.5) найти выражение для коэффициентов характеристического уравнения наблюдателя через параметры матрицы N

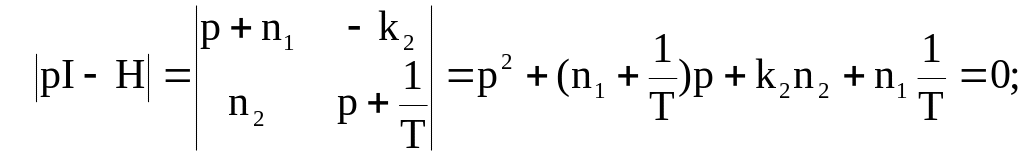
• задаться одной из стандартных форм характеристического уравнения и приравнять коэффициенты характеристических уравнений при одинаковых степенях оператора p уравнения (2.5) и стандартной формы. Выразить неизвестные коэффициенты матрицы N через параметр _n стандартной формы характеристического уравнения наблюдателя, или в конечном счете, через желаемое быстродействие и перерегулирование. Для примера возьмем биномиальное распределение

p² + 2_nр +_n² =0.

Тогда искомые коэффициенты наблюдателя будут равны

Значение параметра _n и значение  стандартной формы характеристического уравнения модального регулятора (пункт 1.2.) должны находится в соотношении _n =(1,52,0), чтобы обеспечить более высокое быстродействие работы наблюдателя по сравнению с управляемой системой. Учитывая условие обеспечения более высокого быстродействия наблюдателя, примем: _n =1,5 рад/с; t_p = 3/ = 0,3 с; к₁ = 10; к₂ = 0,1; Т = 0,2 с. Тогда численные значения коэффициентов наблюдателя будут: n₁ = 25; n₂ = 1000.

Запишем в скалярном виде уравнения системы модального управления с наблюдателем:

(2.7)

По полученным в скалярной форме уравнениям (2.7) разработана структурная схема системы с числовыми данными (рис.2.2). Коэффициенты наблюдателя и модального регулятора выбраны с использованием биномиального распределения.

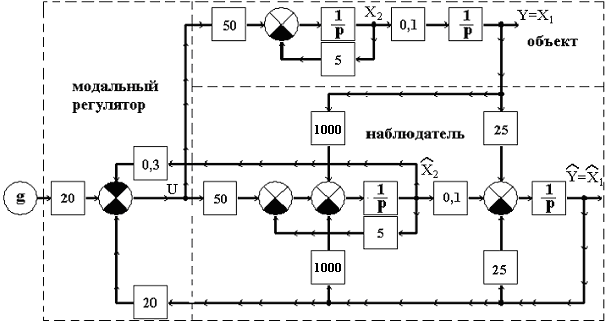
Рис.2.2

На рис.2.3 представлены результаты моделирования системы модального управления с наблюдателем в среде пакета прикладных программ SyAn. На графиках приведены переходные процессы при g(t) = 1 для биномиального распределения.

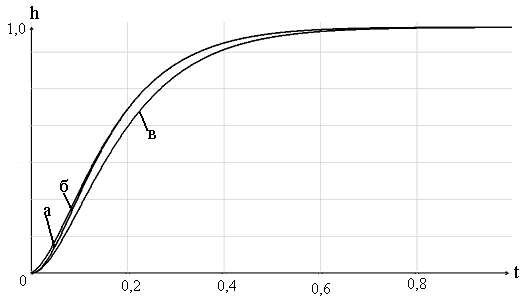
Рис.2.3

Из графиков рис.2.3 видно, что сходимость переменных состояния наблюдателя и переменных состояния объекта достаточно высокая (графики а и б) и быстрая. Кроме того, быстродействие системы модального управления с наблюдателем несколько выше, чем в системе без наблюдателя (график в).

Библиографический список

1. Теория автоматического управления: учебник для машиностроит. спец. вузов/под ред. Ю. М. Соломенцева.-3-е изд., стер..-М.:Высш. шк., 2000.-268 с.:ил.

2. Ерофеев,А.А. Теория автоматического управления: учебник для вузов по направлениям: «Автоматизация и упр.», «Систем. анализ и упр.»/А.А.Ерофеев. – 2-е изд. доп. и перераб.. - СПб.: Политехника, 2005. - 302 с.: ил.

3. Ротач,В.Я. Теория автоматического управления: учебник для вузов по специальности «Автоматизация технолог. процессов и пр-в (энергетика)»/ В.Я.Ротач . – 3-е изд., стер.. - М.: МЭИ, 2005. –399 с.: ил.

4. Бакаев, В.Н. Теория автоматического управления: учеб. пособие / В.Н. Бакаев. -изд. 2-е перераб. и доп. -Вологда: ВоГТУ, 2004.- 190 с.

5. Бакаев, В.Н. Методические указания к практическим занятиям по курсу «Моделирование систем» / В.Н. Бакаев. -Вологда: ВоГТУ, 2011.- 36 с.

6. Топчеев, Ю.И. Атлас для проектирования систем автоматического регулирования/Ю.И. Топчеев. -М.: Машиностроение, 1989.-752с.

7. Советов, Б.Я. Моделирование систем: учеб. для вузов – 3-е изд., перераб. и доп./Б.Я.Советов, С.А.Яковлев. – М.: Высш. шк., 2001. –343 с.

8. Коршунов, Ю.М. Математические основы кибернетики: учеб. пособие для вузов/Ю.М.Коршунов. - М.: Энергоатомиздат, 1987.- 496 с.

9. Востриков, А.С. Теория автоматического управления: учеб. пособие для вузов по направлению « Автоматизация и упр.»/ А.С.Востриков, Г.А.Французова. - изд. 2-е, стер.. -М.: Высш. шк., 2006.-365с.

10. Основы теории управления: учеб. пособие для вузов по специальности «Гос. и муниципал. упр.»/под ред. В.Н.Парахиной, Л.И.Ушвицкого. – Финансы и статистика, 2003. - 558 с.: ил.

11. Егоров,А.И. Основы теории управления/А.И.Егоров. - М.: Физматгиз, 2004. - 502 с.: ил.

12. Официальный сайт МИРЕА. Режим доступа: http://www.cpd.mirea.ru/