1.2. Пример расчета модального регулятора

Рассмотрим задачу синтеза обратной связи для системы управления электроприводом перемещения. Пусть упрощенная линейная модель разомкнутой системы управления описывается дифференциальным уравнением вида

где: Т – постоянная времени привода, учитывающая его инерционность; к – общий статический коэффициент передачи канала управления;  и  – соответственно угол поворота и угловая скорость электродвигателя; u - управляющий сигнал (напряжение управляемого источника питания).

Переходя к изображениям по Лапласу, получим

где к₁к₂ = к. Представим объект управления структурной схемой в виде последовательного соединения апериодического и интегрирующего звеньев рис.1.1.

Рис.1.1

Уравнения объекта в скалярной форме будут иметь вид

Здесь - переменная состояния, пропорциональная углу поворота электропривода; - переменная состояния, пропорциональная угловой скорости электропривода.

Уравнение объекта в векторно-матричной форме согласно (1.1)

Отсюда находим

Корни характеристического уравнения разомкнутой системы следовательно, объект управления является нейтральным. Для обеспечения заданного перемещения введем линейные обратные связи по углу и угловой скорости

u(t) = – l₁ x₁(t) – l₂ x₂(t) + k₀ g(t),

где g – задаваемое значение перемещения.

Тогда замкнутая система с модальным управлением будет иметь вид, показанный на рис.1.2.

Рис.1.2

Она описывается дифференциальными уравнениями в скалярной форме

(1.7)

Коэффициент усиления предварительного усилителя К₀ найдем из условия обеспечения установившегося перемещения (заданного), т.е. y=x₁=g. При этом

Тогда из уравнения (1.7) получим К₀ = l_1.

Характеристическое уравнение замкнутой САУ с неизвестными параметрами l_i модального регулятора найдем из уравнения (1.7)

(1.8)

Если для САУ второго порядка принять коэффициенты желаемого характеристического уравнения (1.7) в соответствии с распределением Баттерворта, т. е.

D(p) = p² +1,4  p + ² = 0 и t_p =3/, (1.9)

то предварительно задавшись требуемым временем переходного процесса t_p, приравнивая коэффициенты при одинаковых степенях оператора р в уравнениях (1.8) и (1.9), получим следующие коэффициенты обратных связей (модального регулятора):

(1.10)

Если для САУ второго порядка принять коэффициенты желаемого характеристического уравнения (1.7) в соответствии с биномиальным распределением , т. е.

D(p) = p² +2  p + ² = 0 и t_p  3/, (1.11)

то предварительно задавшись требуемым временем переходного процесса t_p, приравнивая коэффициенты при одинаковых степенях оператора р в уравнениях (1.8) и (1.11), получим следующие коэффициенты обратных связей (модального регулятора):

(1.12)

Для приведенной САУ модального управления примем следующие значения параметров: T=0,2 c.; k₁=10; k₂=0,1; t_p=0,3 c. Тогда коэффициенты обратных связей модального регулятора, рассчитанные по формулам (1.10) и (1.12), будут иметь значения:

- для биномиального распределения - l₁= 20; l₂= 0,3;

- для распределения Баттерворта - l₁= 20; l₂= 0,18.

Рис.1.3

На рис.1.3 приведена схема модели системы управления с модальным регулятором, настроенным на распределение Баттерворта.

На рис. 1.4 приведены результаты моделирования САУ с модальным управлением в среде пакета прикладных программ SyAn. На графиках приведены переходные процессы при g(t) = 1 для биномиального распределения (рис.1.4,а) и для распределения Баттерворта (рис.1.4,б).

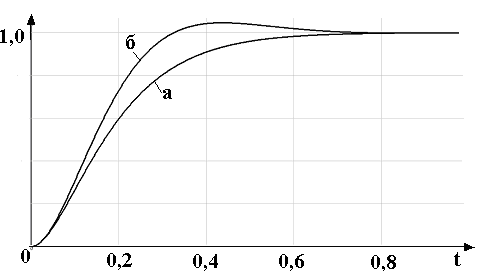
Рис.1.4

При использовании распределения Баттерворта время переходного процесса меньше, чем при использовании биномиальной настройки, но в тоже время появляется перерегулирование. При использовании биномиальной стандартной настройки и стандартного распределения Баттерворта ошибка системы регулирования с нейтральным объектом стремится к нулю. В обоих случаях быстродействие выше, чем при классических оптимальных настройках регуляторов (модульной и симметричной).