Лінійна інтерполяція та інтерполяція кубічним сплайном
Лінійною
інтерполяцією називають інтерполяцію
алгебраїчним двочленом
функції
,
заданої у двох крапках
і
відрізка
.
У випадку якщо задані значення в декількох
крапках, функція заміняється
кусочно-лінійною функцією.
Для одномірної інтерполяції таблично заданих функцій в Matlab використовується функція interp1(x,y,xi), яка повертає вектор yi, що містить елементи, відповідні до елементів xi і отримані лінійною інтерполяцією векторів x і y.
Виконаємо
інтерполяцію функції
графік, що й відображає, отриманої
функції:
>> x=[0:0.5:5];
>> y=exp(sin(x));
>> xi=[0:0.01:5];
>> yi=interp1(x,y,xi);
>> plot(x,y,'*',xi,yi);
Рисунок 3.5 – Графік інтерполюючої функції
Так як при лінійній інтерполяції крапки просто послідовно з'єднуються відрізками прямих, графік кривої, що інтерполює, виходить не гладким. У цьому випадку, набагато кращі результати може дати сплайн-інтерполяція.
В Matlab кубічна сплайн-інтерполяція реалізується наступною функцією:
yi = spline(x,y,xi) — використовує вектори х і y аргументи, що містять, функції і її значення, і вектор xi, що задає нові крапки; для знаходження елементів вектора yi використовується кубічна сплайн-інтерполяція;
рр = spline(x.y) — повертає рр-форму сплайна, використовувану у функції ppval і інших сплайн-функціях.
Реалізація сплайн-інтерполяції функції :
>> x=[0:5];
>> y=exp(sin(x));
>> xi=[0:0.1:5];
>> yi=spline(x,y,xi);
>> plot(x,y,'*',xi,yi);
Рисунок 3.6 – Інтерполяція сплайнами
Наближення функцій за допомогою Basic Fitting
Використовуючи лінійну й поліноміальну апроксимації, одержати емпіричні формули для функції y=f(x) , заданої в табличному вигляді:
>> x=[0.75,1.50,2.25,3.00,3.75]
>> y=[2.50,1.20,1.12,2.25,4.28]
>> plot(x,y,'o')
Графік зображено на малюнку:
Для запуску Basic Fitting потрібно перейти до підменю Tools.
Рисунок 3.7 – Вихідні дані для розрахунків
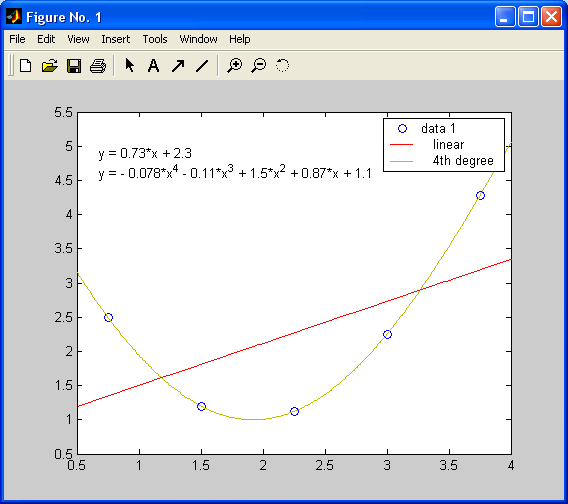
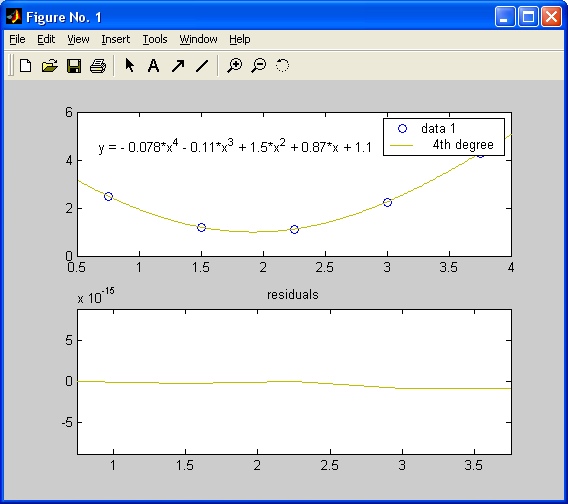
Рисунок 3.8 – Приклад застосування Basic Fitting для визначення функції наближення
Завдання
Згідно свого варіанту визначити апроксимуючу або інтерполюючу функцію для приведених в таблиці даних наступними способами:
Поліноміальна апроксимація.
Інтерполяція рядом Фур’є.
Лінійна інтерполяція.
Інтерполяція кубічними сплайнами.
Дослідити можливості блоку Basic Fitting, використовуючи різні способи наближення.
Порівняти результати розрахунків. Зробити висновки.
Варіанти завдань
Зміст звіту
Звіт з роботи складається з наступних пунктів:
Тема та мета роботи.
Кроткі теоретичні відомості.
Результати використання кожного з видів наближення, що вказано у завданні, для варіанту студента у вигляді програми та графіків.
Висновки