Учет инфляции и налогов при начислении процентов

Во всех рассмотренных выше случаях мы не учитывали влияние на параметры сделки инфляции и налогов. В условиях реального снижения покупательной способности денег рассмотрим механизмы этого влияния на результаты финансовых операций.

1. Инфляция

Инфляция характеризуется обесцениванием национальной валюты (т.е. снижением ее покупательной способности) и общим повышением цен в стране. Очевидно, что в различных случаях влияние инфляционного процесса сказывается на договаривающихся сторонах неодинаково: когда кредитор теряет часть дохода за счет обесценивания денежных средств, дебитор получает возможность выиграть на том, что может погасить долг деньгами меньшей покупательной способности. Инфляцию необходимо учитывать при расчете наращенной и текущей сумм денег, а также при определении доходности какой-либо финансовой операции.

Пусть S – наращенная сумма денег, измеренная по номиналу, S – эта же сумма с учетом инфляции. Тогда 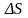будет обозначать разницу между этими суммами.

Отношение 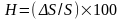, выраженное в процентах, называется уровнем инфляции.

При расчетах используют относительную величину уровня инфляции – темп инфляции , причем

.

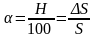Тогда для определения S получим выражение:

.

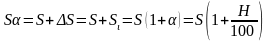Величину 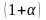, показывающую, во сколько раз S больше S (т.е. во сколько раз выросли цены), называют индексом инфляции J_и , т.е.

.

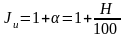(Индекс инфляции J_и называют еще индексом цен.)

Например, если уровень инфляции равен 50%, то цены выросли в полтора раза.

В свою очередь:

, .

Напомним, что изменение покупательной способности денег за некоторый период измеряется с помощью индекса J_пс, который равен обратной величине индекса инфляции:

.

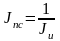При этом .

Следует отметить, что индексы J_и и J_пс относятся к одному и тому же временному интервалу. Пусть в настоящий момент получено 100 тыс. руб. и известно, что за два предшествующих года цены увеличились в два раза, т.е. J_и = 2. В этом случае индекс покупательной способности денег равен 1/2 Следовательно, реальная покупательская способность 100 тыс. руб. составит в момент получения всего 100(1/2) =50 тыс. руб. в деньгах двухлетней давности.

Динамика индекса инфляции за некоторый период отражает изменения в экономических процессах за это время. Понятно, что повышение индекса инфляции за определенный период, по сравнению с предыдущим таким же периодом, указывает на ускорение инфляции (и, соответственно, на снижение покупательской способности), снижение – на уменьшение ее темпов.

Среднегодовые темпы роста цен i_и и уровень инфляции Н находятся из величины J_и:

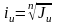; Н= .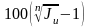

Если Н – прогнозируемый уровень инфляции за период, то за n периодов имеем:

.

Наиболее часто встречающаяся (грубая) ошибка в финансово-экономических расчетах – это простое суммирование темпов инфляции для получения обобщающего показателя за весь период. Например, пусть цены каждый месяц растут на 4%. Тогда за годовой уровень инфляции принимают величину 124=48%. Такие расчеты часто используют банки и финансовые компании, привлекая клиентов вкладывать средства, к примеру, под 60% годовых. Между тем, если уровень инфляции составляет 4% в месяц, то это означает, что за месяц цены вырастут в 1+0,04=1,04 раза, а за год – в 1,04¹²=1,665 раза. Значит, годовой индекс инфляции составляет 1,665-1=0,665, т.е. годовой уровень инфляции составляет 66,5%. После такого расчета процентная ставка в 60% годовых, мягко говоря, теряет свою привлекательность.

В общем виде индекс цен за несколько неодинаковых периодов равен произведению индексов цен цепочки периодов:

.

Это означает, что цены в текущем периоде повышаются на Н_t процентов относительно уровня, сложившегося в предыдущем периоде.

Пример 1. Постоянный темп инфляции имеет уровень: а) 3% в месяц; б). имеет место последовательный прирост цен по месяцам: 5, 4 и 3%. Найти годовой уровень инфляции и темп инфляции за 3 месяца.

Решение. а) по формуле (2.43) найдем индекс цен .

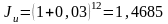Тогда годовой уровень инфляции вычисляем по формуле (2.42):

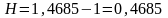, т.е. 46,85%, а не 12*0,03=0,36, т.е. 36%.

б) Индекс цен за три месяца, согласно формуле (2.44), равен:

1,051,041,03=1,1248. Тогда уровень инфляции за 3 месяца составит 1,1248-1=0,1248, т.е. 12,48%.

Рассмотрим, до какой же степени могут обесцениться деньги при операции наращения. Последнее, как обычно, производится по простой и сложной ставке процентов. Если взять простую ставку, то, подставляя соответствующий множитель наращения в формулу (2.41), получим:

.

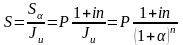Из (2.45) видно, что реальное увеличение суммы будет иногда, когда множитель наращения простых процентов будет больше, чем индекс инфляции.

Если наращение производится по сложной ставке процентов, то найдем:

.

Множители наращения с учетом инфляции для простых и сложных процентов будут:

; .

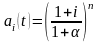Проанализируем, при каких соотношениях между i и можно надеяться на реальный рост доходов. Если среднегодовой темп инфляции равен ставке i процентов ( =i), то множитель наращения равен единице и роста реальной суммы не будет. Тогда S=P, и в этом случае говорят, что инфляция съедает наращение.

Если > i, будет «эрозия» капитала (рис. 1), при < i происходит рост реальной суммы. Ставка, большая, чем , называется ставкой процента.

Для простых процентов минимально допустимую процентную ставку найдем, приравнивая единице множитель наращения: 1+it=(1+ )ⁿ=J_и. Отсюда .

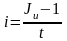При данной процентной ставке наращение по простым процентам будет полностью компенсировать инфляцию.

Пример 2. Пусть на сумму 150 тыс. руб. в течение трех месяцев начисляются простые проценты по ставке 50% годовых. Найти наращенную сумму с учетом обесценивания и минимально допустимую величину ставки, если индекс цен за 3 месяца составляет 1,1250 (пример 1).

Решение. тыс. руб.