Питання для контролю вивченого матеріалу

1. Що таке тіло обертання ?

2. Записати формулу для обчислення об’єму тіла, обмеженого кривою y=f(x) і прямими x=a, x=b, y=0.

3. Як обчислюється об’єм тіла, обмеженого кривими y=f₁(x) і y=f₂(x), f₂(x)≥f₁(x)≥0 і прямими x=а, x=в?

4. Обчислити об’єм тіла, утвореного обертанням навколо вісі Ох фігури, обмеженої лініями y=x³, y=0, x=0, x=2.

Література

1. Соколенко О.І. Вища математика: Підручник – К.: Видавничий центр „Академія”, 2002. – 432с.

2. Валуцэ И.И. Дилигул Г.Д. Математика для техникумов на базе средней школы: Учебное пособие. – 2-е изд., перераб. и доп. – М.: Наука, 1990. – 576с.

3. Дюженкова Л.І., Носаль Т.В. Вища математика: Практикум: Навчальний посібник. – К.: Вища школа, 1991. – 407с.: іл.

Тема 5: Площа поверхні обертання.

1. Площа поверхні обертання.

2. Розв’язування типових задач.

Короткі теоретичні відомості

Площа поверхні, що утворюється при обертанні навколо вісі Ох кривої y=f(x), а≤х≤b, f(x)≥0, обчислюється за формулою

(1)

де функції і ` неперервні на відрізку [a;b].

Якщо криву АВ задано параметрично рівняннями , де функції неперервні на [α, β], то

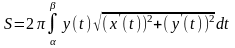, (2)

причому значення α параметра t відповідає точці А, а значення β-точці В.

Типові задачі

1. Обчислити площу поверхні, утвореної обертанням навколо вісі Ох однієї арки циклоїди .

За формулою (2) дістаємо

2. Обчислити площу поверхні, утвореної обертанням навколо вісі дуги кубічної параболи y=x³,обмеженої точками О(0;0) та А( .

Знаходимо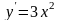 . За формулою (1) маємо

Питання для контролю вивченого матеріалу

1. Як обчислити площу поверхні, утвореної обертанням навколо вісі Ох кривої ?

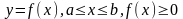2. За якою формулою обчислюється поверхня, якщо криву задано параметрично?

3. Обчислити площі поверхонь, утворених обертанням навколо вісі Ох таких кривих:

   • параболи y²=x+2 від вершини до точки з абсцисою х=0, y0;

   • дуги синусоїди від х=0 до х=1;

   • дуги астроїди х=cos³ t, y=sin³ t, .

Література

1. Соколенко О.І. Вища математика: Підручник – К.: Видавничий центр „Академія”, 2002. – 432с.

2. Валуцэ И.И. Дилигул Г.Д. Математика для техникумов на базе средней школы: Учебное пособие. – 2-е изд., перераб. и доп. – М.: Наука, 1990. – 576с.

3. Дюженкова Л.І., Носаль Т.В. Вища математика: Практикум: Навчальний посібник. – К.: Вища школа, 1991. – 407с.: іл.

Тема 6: Довжина дуги кривої.

1. Поняття довжини дуги.

2. Обчислення довжини дуги кривої.

Короткі теоретичні відомості

М₁ М₂

А

B

Довжиною L дуги АВ називається границя, до якої прямує периметр Р_n вписаної в цю дугу ламаної, коли кількість n її ланок необмежено зростає, а найбільша із довжин S її ланок прямує до нуля: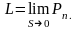

Якщо функції 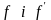неперервні на відрізку [a;b], то довжина відповідної дуги кривої

(1)

Якщо криву АВ задано параметрично рівняннями x=x(t), y=y(t), , де функції неперервні на , причому точці А відповідає значення параметра 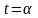,а точці В-значення , то довжина цієї кривої

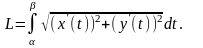(2)

Якщо криву задано в полярних координатах рівнянням 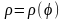, , то її довжина

(3)

де функції 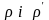неперервні на відрізку

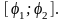
Приклад 1. Обчислити довжину напівкубічної параболи у²=х³ між точками з абсцисами х=1 і x=2.

Диференціюючи рівняння кривої, знаходимо

Тоді за формулою(1) .

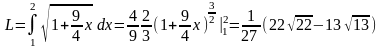Приклад 2. Обчислити довжину кардіоїди .

Задана крива симетрична відносно полярної вісі, тому при зміні кута

від 0 до 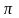полярний радіус опише половину кривої. Оскільки , обчислюємо за формулою (3) довжину кривої.