Література.

1. Валуцэ И.И., Дилигул І.Д. Математика для техникумов на базе средней школы: Учеб. пособие.-2-е изд., перераб. и доп.- М .:Наука, 1991-576с.:ил.

2. Лисичкин В.Т., Соловейчик И.Л Математика: Учеб. пособие для техникумов –М.: Высшая школа,1991-480 с.

3. Соколенко О.І Вища математика: Підручник -К.: Видавничий центр „Академія”,2002-432с.

4. Дюженкова Л.І.Носаль Т.В Вища математика: Практикум: Навч. посібник. -К.: Вища школа, 1991-407с.:іл.

Тема 2: Інтегрування дробово - раціональних функцій.

1. Поняття дробово - раціональної функції.

2. Інтегрування дробово - раціональних функцій.

Короткі теоретичні відомості

Функція вигляду F(x)= P(x)/Q(X), де P(x) і Q(x) - многочлени називається дробово – раціональною, або раціональним дробом. Дріб правильний , якщо степінь многочлена P(x) нижчий за степінь Q(x). Якщо дріб неправильний, з нього виділяють цілу частину (многочлен), ділячи чисельник на знаменник: .

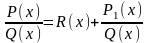Правильний дріб можна подати у вигляді суми скінченого числа елементарних дробів типу:

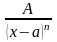I) ; II) ; III) ; IV) , де n>1 – натуральне число, .

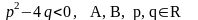Інтеграли від елементарних дробів обчислюємо за формулами:

I. . (1)

II. . (2)

III. Якщо чисельник дробу пропорційний похідній знаменника, то інтеграл обчислюють за формулою . (3)

В іншому разі чисельник розкладають на суму двох доданків, один з яких пропорційний похідній тричлена, а другий – сталій. Тоді інтеграл записуємо у вигляді суми двох інтегралів, перший з яких обчислюємо за формулою (3), а другий зводимо до інтеграла , виділенням повного квадрата з тричлена.

IV. Інтеграл від цього дробу зводиться до двох інтегралів, перший з яких табличний типу , а другий . Останній шляхом (n-1)- кратного інтегрування зводиться до табличного 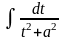за допомогою рекурентної формули (4)

Отже, інтегрування кожного раціонального дробу можна звести до інтегрування суми елементарних дробів за таким правилом:

1. Якщо дріб неправильний то, виділивши цілу частину , записати його у вигляді .

2. Розкласти знаменник .

3. Зобразити дріб 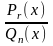у вигляді суми елементарних дробів ,

де А₁,...,A_k,…,B₁,C₁,…,B₂,C₂,…- деякі сталі ,k,…,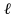 ,…-натуральні числа, більші за одиницю, причому .

4. Обчислити невизначені коефіцієнти А₁, ... , С_l. Для цього потрібно звести останню рівність до спільного знаменника, і прирівняти чисельники в обох частинах рівності. Невідомі коефіцієнти можна обчислити двома способами: а) прирівнюванням коефіцієнтів при однакових степенях в обох частинах рівності; б) наданням змінній конкретних значень. Часто застосовують комбінацію цих способів; залишається розв’язати систему лінійних рівнянь з 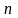невідомими A₁,...

5. Обчислити заданий інтеграл, використовуючи схему розкладу і значення невідомих коефіцієнтів.

Приклад. Обчислити інтеграл .

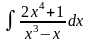Виділимо частину підінтегрального дробу .

Розкладемо знаменник на множники:

x³-x=x(x-1)(x+1). Зобразимо дріб у вигляді суми елементарних дробів .

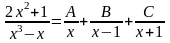Останню рівність зведемо до спільного знаменника і прирівняємо чисельники: .

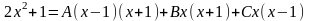Оскільки числа 0,1,-1 є коренями знаменника, то коефіцієнти А, В, С зручно обчислити підставляючи саме ці значення в останню рівність. При х=0 дістаємо 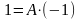тобто А=-1; при х=1 маємо 3=2В, тобто В=3/2 ; при х = -1 дістаємо 3=2С , C=3/2.

Обчислюємо заданий інтеграл , враховуючи значення заданих коефіцієнтів і попередній розклад: .
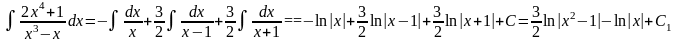